Example 5.6

EXAMPLE 5.6 The Probability Histogram

CASE 5.1 Suppose that the quality engineer chooses just 15 switches for inspection. What is the probability that no more than one of the 15 is nonconforming? The count of nonconforming switches in the sample has approximately the distribution. Figure 5.2 is a probability histogram for this distribution. The distribution is strongly skewed. Although can take any whole-number value from 0 to 15, the probabilities of values larger than 5 are so small that they do not appear in the histogram.


		.08
15	0	.2863
	1	.3734
	2	.2273
	3	.0857
	4	.0223
	5	.0043
	6	.0006
	7	.0001
	8
	9

We want to calculate

when has the distribution. To use Table C for this calculation, look opposite and under . This part of the table appears at the left. The entry opposite each is . Blank entries are 0 to four decimal places, so we have omitted most of them here. From Table C,

249

Figure 5.2: FIGURE 5.2 Probability histogram for the binomial distribution with and , Example 5.6.

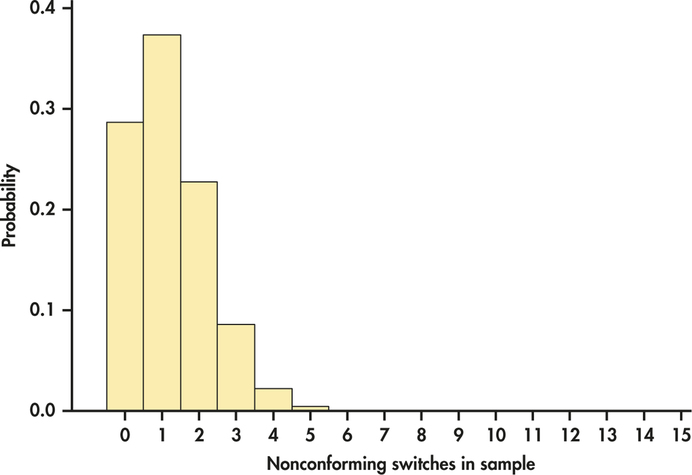
About two-thirds of all samples will contain no more than one nonconforming switch. In fact, almost 29% of the samples will contain no bad switches. A sample of size 15 cannot be trusted to provide adequate evidence about the presence of nonconforming items in the population. In contrast, for a sample of size 50, there is only a 1.5% risk that no bad switch will be revealed in the sample in light of the fact that 8% of the population is nonconforming. Calculations such as these can used to design acceptable acceptance sampling schemes.