Example 6.18

EXAMPLE 6.18 Bottle Fill Amount: The -Value

CASE 6.1 In Example 6.13, the observations are an SRS of size from a population of bottles with . The observed average fill amount is . In Example 6.17, we found that the test statistic for testing versus is

323

Figure 6.13: FIGURE 6.13 The -value for Example 6.18. The two-sided -value is the probability (when is true) that takes a value as extreme or more extreme than the actual observed value, . Because the alternative hypothesis is two-sided, we use both tails of the distribution.

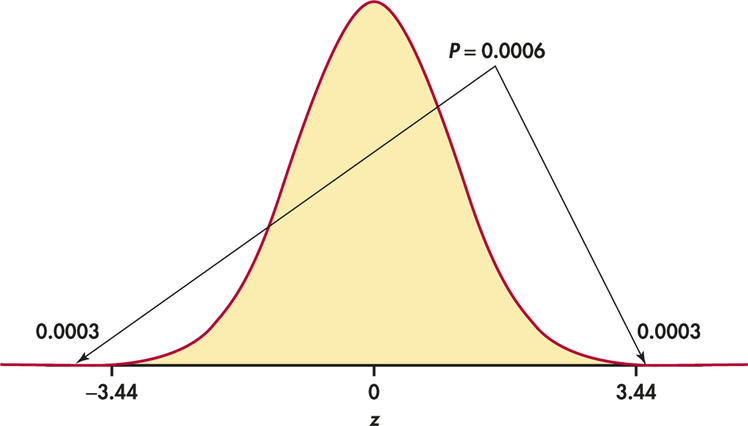
If is true, then is a single observation from the standard Normal, (0,1), distribution. Figure 6.13 illustrates this calculation. The -value is the probability of observing a value of at least as extreme as the one that we observed, . From Table A, our table of standard Normal probabilities, we find

The probability for being extreme in the negative direction is the same:

So the -value is

In Example 6.13 (page 317), we reported a probability of 0.00058 was obtained from software. The value of 0.0006 found from the tables is essentially the same.