Example 6.28

EXAMPLE 6.28 Diameters of Bearings

The diameter of a particular precision ball bearing has a target value of 20 millimeters (mm) with tolerance limits of mm around the target. Suppose that the bearing diameters vary Normally with standard deviation of sixty-five hundred-thousandths of a millimeter, that is, mm. When a shipment of the bearings arrives, the consumer takes an SRS of five bearings from the shipment and measures their diameters. The consumer rejects the bearings if the sample mean diameter is signif-cantly different from 20 mm at the 5% significance level.

This is a test of the hypotheses

To carry out the test, the consumer computes the statistic:

and rejects if

A Type I error is to reject when in fact .

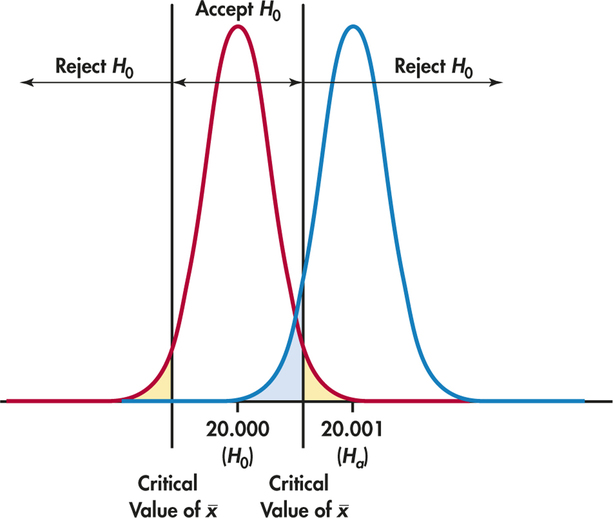
What about Type II errors? Because there are many values of in , we concentrate on one value. Based on the tolerance limits, the producer agrees that if there is evidence that the mean of ball bearings in the lot is 0.001 mm away from the desired mean of 20 mm, then the whole shipment should be rejected. So, a particular Type II error is to accept when in fact .

Figure 6.22 shows how the two probabilities of error are obtained from the two sampling distributions of , for and for . When , is true and to reject is a Type I error. When , accepting is a Type II error. We will now calculate these error probabilities.

Figure 6.22: FIGURE 6.22 The two error probabilities, Example 6.28. The probability of a Type I error (yellow area) is the probability of rejecting when in fact . The probability of a Type II error (blue area) is the probability of accepting when in fact .