14.3 The Power of the ANOVA Test

745

The power of a test is the probability of rejecting when is, in fact, true. Power measures how likely a test is to detect a specific alternative. When planning a study in which ANOVA will be used for the analysis, it is important to perform power calculations to check that the sample sizes are adequate to detect differences among means that are judged to be important. Power calculations also help evaluate and interpret the results of studies in which was not rejected. We sometimes find that the power of the test was so low against reasonable alternatives that there was little chance of obtaining a significant .

Reminder

image

power of the two-sample test, p. 404

In Chapter 7, we found the power for the two-sample test. One-way ANOVA is a generalization of the two-sample test, so it is not surprising that the procedure for calculating power is quite similar. Here are the steps that are needed:

  1. Specify
    1. an alternative that you consider important; that is, values for the true population means
    2. sample sizes in a preliminary study, these are usually all set equal to a common value ;
    3. a level of significance , usually equal to 0.05; and
    4. a guess at the standard deviation .
  2. Find the degrees of freedom and and the critical value that will lead to rejection of . This value, which we denote by , is the upper critical value for the distribution.

  3. Calculate the noncentrality parameter6

    noncentrality parameter

    where is a weighted average of the group means,

    and the weights are proportional to the sample sizes,

  4. Find the power, which is the probability of rejecting when the alternative hypothesis is true—that is, the probability that the observed is greater than . Under , the statistic has a distribution known as the noncentral distribution. This requires special software. SAS, for example, has a function for the noncentral distribution. Using this function, the power is

    noncentral distribution

746

The noncentrality parameter measures how far apart the means are. If the are all equal to a common value is the ordinary average of the and

If the means are all equal (the ANOVA ), then . Large points to an alternative far from , and we expect the ANOVA test to have high power.

Software makes calculation of the power quite easy. The software does Steps 2, 3, and 4, so our task simplifies to just Step 1. Some software doesn’t request the alternative means but rather a difference in means that is judged important. Most software will also assume a constant sample size. Let’s run through an example doing the calculations ourselves and then compare the results with output from two software programs.

EXAMPLE 14.27 The Effect of Fewer Subjects

CASE 14.2 The reading comprehension study described in Case 14.2 had 22 subjects in each group. Suppose that a similar study has only 10 subjects per group. How likely is this study to detect differences in the mean responses that are similar in size to those observed in the actual study?

Based on the results of the actual study, we calculate the power for the alternative , with . The are equal, so is simply the average of the :

The noncentrality parameter is, therefore,

Because there are three groups with 10 observations per group, and . The critical value for is . The power is, therefore,

The chance that we reject the ANOVA at the 5% significance level is only about 35%.

Figure 14.18 shows the power calculation output from JMP and Minitab. For JMP, you specify the alternative means, standard deviation, and the total sample size . The power is calculated when the “Continue” button is clicked. Notice that this result is the same as the result in Example 14.27. For Minitab, you enter the common sample size , standard deviation, and the difference between means that is deemed important. For the alternative means specified in Example 14.27, the largest difference is so that was entered. The power is again the same as the result in Example 14.27. This won’t always be the case. Specifying an important difference will often give a power value that is smaller. This is because it computes a noncentrality parameter that is always less than or equal to the noncentrality value based on knowing all the alternative means.

747

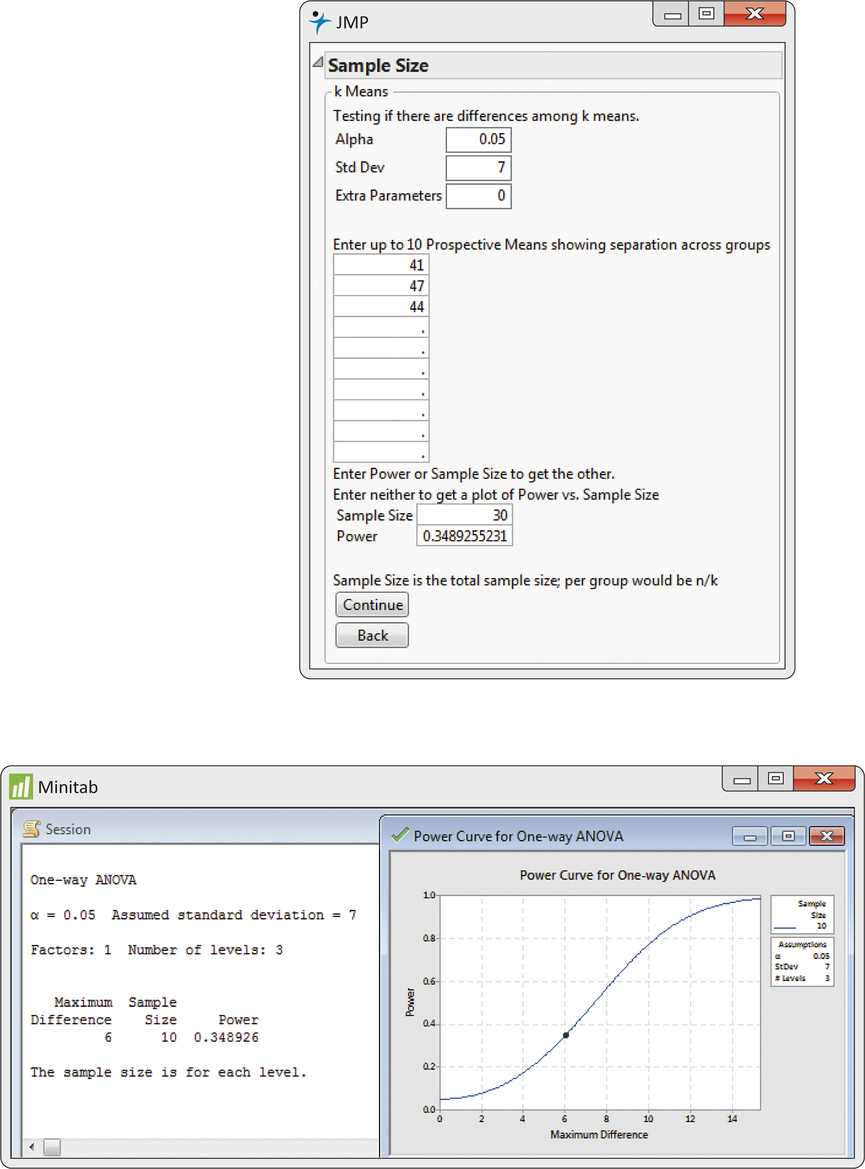
image
Figure 14.18: FIGURE 14.18 JMP and Minitab power calculation outputs, Example 14.27.

748

If the assumed values of the in this example describe differences among the groups that the experimenter wants to detect, then we would want to use more than 10 subjects per group. Although is false for these the chance of rejecting it at the 5% level is only about 35%. This chance can be increased to acceptable levels by increasing the sample sizes.

EXAMPLE 14.28 Choosing the Sample Size for a Future Study

CASE 14.2 To decide on an appropriate sample size for the experiment described in the previous example, we repeat the power calculation for different values of , the number of subjects in each group. Here are the results:

DFG DFE Power
20 2 57 3.16 7.35 0.65
30 2 87 3.10 11.02 0.84
40 2 117 3.07 14.69 0.93
50 2 147 3.06 18.37 0.97
100 2 297 3.03 36.73 ≈ 1

Try using JMP to verify these calculations. With , the experimenters have a 93% chance of rejecting with and thereby demonstrating that the groups have different means. In the long run, 93 out of every 100 such experiments would reject at the level of significance. Using 50 subjects per group increases the chance of finding significance to 97%. With 100 subjects per group, the experimenters are virtually certain to reject . The exact power for is 0.99990. In most real-life situations, the additional cost of increasing the sample size from 50 to 100 subjects per group would not be justified by the relatively small increase in the chance of obtaining statistically significant results.

Apply Your Knowledge

Question 14.30

14.30 Power calculations for planning a study.

You are planning a new eye gaze study for a different university than that studied in Example 14.13 (pages 729–731). From Example 14.13, we know that the standard deviations for the four groups considered in that study were 1.75, 1.72, 1.53, and 1.67. In Figure 14.9, we found the pooled standard error to be 1.68. Because the power of the test decreases as the standard deviation increases, use for the calculations in this exercise. This choice leads to sample sizes that are perhaps a little larger than we need but prevents us from choosing sample sizes that are too small to detect the effects of interest. You would like to conclude that the population means are different when and .

  1. Pick several values for (the number of students that you will select from each group) and calculate the power of the ANOVA test for each of your choices.
  2. Plot the power versus the sample size. Describe the general shape of the plot.
  3. What choice of would you choose for your study? Give reasons for your answer.

Question 14.31

14.31 Power against a different alternative.

Refer to the previous exercise. Suppose we increase to 3.9. For each of the choices of in the previous example, would the power be larger or smaller under this new set of alternative means? Explain your answer.

14.31

The power would be larger. For larger differences between alternative means, gets bigger, increasing our power to see these differences.