SECTION 4.4 Exercises
For Exercises 4.90 and 4.91, see page 212; for 4.92, see page 214; and for 4.93, see page 216.
Question 4.94
CASE 4.24.94 Two day demand.
Refer to the distribution of daily demand for blood bags X in Case 4.2 (pages 210–211). Let Y be the total demand over two days. Assume that demand is independent from day to day.
- List the possible values for Y.
- From the distribution of daily demand, we find that the probability that no bags are demanded on a given day is 0.202. In that light, suppose a hospital manager states, “The chances that no bags are demanded over two consecutive days is 0.404.” Provide a simple argument to the manager explaining the mistake in probability conclusion. (Hint: Use more than two days as the basis for your argument.)
- What is the probability that the total demand over two days is 0? In terms of the random variable, what is P(Y=0)?
Question 4.95
4.95 How many courses?
At a small liberal arts college, students can register for one to six courses. In a typical fall semester, 5% take one course, 5% take two courses, 13% take three courses, 26% take four courses, 36% take five courses, and 15% take six courses. Let X be the number of courses taken in the fall by a randomly selected student from this college. Describe the probability distribution of this random variable.
Question 4.96
4.96 Make a graphical display.
Refer to the previous exercise. Use a probability histogram to provide a graphical description of the distribution of X.
Question 4.97
4.97 Find some probabilities.
Refer to Exercise 4.95.
- Find the probability that a randomly selected student takes three or fewer courses.
- Find the probability that a randomly selected student takes four or five courses.
- Find the probability that a randomly selected student takes eight courses.
4.97
(a) 0.23. (b) 0.62. (c) 0.
Question 4.98
4.98 Texas hold 'em.
The game of Texas hold 'em starts with each player receiving two cards. Here is the probability distribution for the number of aces in two-card hands:
| Number of aces | 0 | 1 | 2 |
| Probability | 0.8507 | 0.1448 | 0.0045 |
- Verify that this assignment of probabilities satisfies the requirement that the sum of the probabilities for a discrete distribution must be 1.
- Make a probability histogram for this distribution.
- What is the probability that a hand contains at least one ace? Show two different ways to calculate this probability.
Question 4.99
4.99 How large are households?
Choose an American household at random, and let X be the number of persons living in the household. If we ignore the few households with more than seven inhabitants, the probability model for X is as follows:
| Household size X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Probability | 0.27 | 0.33 | 0.16 | 0.14 | 0.06 | 0.03 | 0.01 |
- Verify that this is a legitimate probability distribution.
- What is P(X≥5)?
- What is P(X>5)?
- What is P(2<X≤4)?
- What is P(X≠1)?
- Write the event that a randomly chosen household contains more than two persons in terms of X. What is the probability of this event?
4.99
(a) Verify that probabilities add to 1. All probabilities are between 0 and 1. (b) 0.10. (c) 0.04. (d) 0.30. (e) 0.73. (f) P(X>2)=0.40.
Question 4.100
CASE 4.24.100 How much to order?
Faced with the demand for the perishable product in blood, hospital managers need to establish an ordering policy that deals with the trade-off between shortage and wastage. As it turns out, this scenario, referred to as a single-period inventory problem, is well known in the area of operations management, and there is an optimal policy. What we need to know is the per item cost of being short (CS)and the per item cost of being in excess (CE). In terms of the blood example, the hospital estimates that for every bag short, there is a cost of $80 per bag, which includes expediting and emergency delivery costs. Any transfusion blood bags left in excess at day's end are associated with $20 per bag cost, which includes the original cost of purchase along with end-of-day handling costs. With the objective of minimizing long-term average costs, the following critical ratio (CR) needs to be computed:
CR=CSCS+CE
Recognize that CR will always be in the range of 0 to 1. It turns out that the optimal number of items to order is the smallest value of k such that P(X≤k) is at least the CR value.
- Based on the given values of CS and CE, what is the value of CR?Page 218
- Given the CR found in part (a) and the distribution of blood bag demand (page 211), determine the optimal order quantity of blood bags per day.
- Keeping CE at $20, for what range of values of CS does the hospital order three bags?
Question 4.101
4.101 Discrete or continuous?
In each of the following situations, decide whether the random variable is discrete or continuous, and give a reason for your answer.
- Your web page has five different links, and a user can click on one of the links or can leave the page. You record the length of time that a user spends on the web page before clicking one of the links or leaving the page.
- The number of hits on your web page.
- The yearly income of a visitor to your web page.
4.101
(a) Time is continuous. (b) Hits are discrete (you can count them). (c) Yearly income is discrete (you can count money).
Question 4.102
4.102 Use the uniform distribution.
Suppose that a random variable X follows the uniform distribution described in Example 4.26 (pages 213–214). For each of the following events, find the probability and illustrate your calculations with a sketch of the density curve similar to the ones in Figure 4.12 (page 214).
- The probability that X is less than 0.1.
- The probability that X is greater than or equal to 0.8.
- The probability that X is less than 0.7 and greater than 0.5.
- The probability that X is 0.5.
Question 4.103
4.103 Spell-checking software.
Spell-checking software catches “nonword errors,” which are strings of letters that are not words, as when “the” is typed as “eth.” When undergraduates are asked to write a 250-word essay (without spell-checking), the number X of nonword errors has the following distribution:
| Value of X | 0 | 1 | 2 | 3 | 4 |
| Probability | 0.1 | 0.3 | 0.3 | 0.2 | 0.1 |
- Sketch the probability distribution for this random variable.
- Write the event “at least one nonword error” in terms of X. What is the probability of this event?
- Describe the event X≤2 in words. What is its probability? What is the probability that X<2?
4.103
(b) P(X≥1)=0.9. (c) “At most, two nonword errors.” P(X≤2)=0.7. P(X<2)=0.4.
Question 4.104
4.104 Find the probabilities.
Let the random variable X be a random number with the uniform density curve in Figure 4.12 (page 214). Find the following probabilities:
- P(X≥0.30).
- P(X=0.30).
- P(0.30<X<1.30).
- P(0.20≤X≤0.25 or 0.7≤X≤0.9).
- X is not in the interval 0.4 to 0.7.
Question 4.105
4.105 Uniform numbers between 0 and 2.
Many random number generators allow users to specify the range of the random numbers to be produced. Suppose that you specify that the range is to be all numbers between 0 and 2. Call the random number generated Y. Then the density curve of the random variable Y has constant height between 0 and 2, and height 0 elsewhere.
- What is the height of the density curve between 0 and 2? Draw a graph of the density curve.
- Use your graph from part (a) and the fact that probability is area under the curve to find P(Y≤1.6).
- Find P(0.5<Y<1.7).
- Find P(Y≥0.95).
4.105
(a) 1/2. (b) 0.8. (c) 0.6. (d) 0.525.
Question 4.106
4.106 The sum of two uniform random numbers.
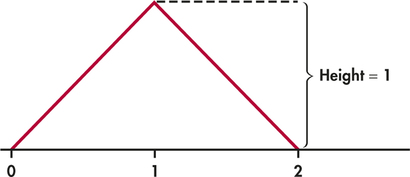
Generate two random numbers between 0 and 1 and take Y to be their sum. Then Y is a continuous random variable that can take any value between 0 and 2. The density curve of Y is the triangle shown in Figure 4.15.
- Verify by geometry that the area under this curve is 1.
- What is the probability that Y is less than 1? (Sketch the density curve, shade the area that represents the probability, then find that area. Do this for part (c) also.)
- What is the probability that Y is greater than 0.6?
Question 4.107
4.107 How many close friends?
How many close friends do you have? Suppose that the number of close friends adults claim to have varies from person to person with mean μ=9 and standard deviation σ=2.4. An opinion poll asks this question of an SRS of 1100 adults. We see in Chapter 6 that, in this situation, the sample mean response ˉx has approximately the Normal distribution with mean 9 and standard deviation 0.0724. What is P(8≤ˉx≤10), the probability that the statistic ˉx estimates μ to within ±1?
4.107
The probability is essentially 1.
Question 4.108
4.108 Normal approximation for a sample proportion.
A sample survey contacted an SRS of 700 registered voters in Oregon shortly after an election and asked respondents whether they had voted. Voter records show that 56% of registered voters had actually voted. We see in the next chapter that in this situation the proportion of the sample ˆp who voted has approximately the Normal distribution with mean μ=0.56 and standard deviation σ=0.019.
- If the respondents answer truthfully, what is P(0.52≤ˆp≤0.60)? This is the probability that the sample proportion ˆp estimates the mean of 0.56 within plus or minus 0.04.
- In fact, 72% of the respondents said they had voted (ˆp=0.72). If respondents answer truthfully, what is P(ˆp≥0.72)? This probability is so small that it is good evidence that some people who did not vote claimed that they did vote.