7.2 Comparing Two Means
 This page includes Video Technology Manuals
This page includes Video Technology Manuals This page includes Statistical Videos
This page includes Statistical VideosHow do retail companies that fail differ from those that succeed? An accounting professor compares two samples of retail companies: one sample of failed retail companies and one of retail companies that are still active. Which of two incentive packages will lead to higher use of a bank’s credit cards? The bank designs an experiment where credit card customers are assigned at random to receive one or the other incentive package. Two-sample problems such as these are among the most common situations encountered in statistical practice.
Two-Sample Problems
- The goal of inference is to compare the means of the response variable in two groups.
- Each group is considered to be a sample from a distinct population.
- The responses in each group are independent of each other and those in the other group.

You must carefully distinguish two-sample problems from the matched pairs designs studied earlier. In two-sample problems, there is no matching of the units in the two samples, and the two samples may be of different sizes. As a result, inference procedures for two-sample data differ from those for matched pairs.
We can present two-sample data graphically with a back-to-back stemplot for small samples (page 17) or with side-by-side boxplots for larger samples (page 29). Now we will apply the ideas of formal inference in this setting. When both population distributions are symmetric, and especially when they are at least approximately Normal, a comparison of the mean responses in the two populations is most often the goal of inference.
We have two independent samples, from two distinct populations (such as failed companies and active companies). We measure the same quantitative response variable (such as the cash flow margin) in both samples. We will call the variable x1 in the first population and x2 in the second because the variable may have different distributions in the two populations. Here is the notation that we will use to describe the two populations:
| Population | Variable | Mean | Standard deviation |
|---|---|---|---|
| 1 | x1 | μ1 | σ1 |
| 2 | x2 | μ2 | σ2 |
We want to compare the two population means, either by giving a confidence interval for μ1−μ2 or by testing the hypothesis of no difference, H0:μ1=μ2. We base inference on two independent SRSs, one from each population. Here is the notation that describes the samples:
| Population | Sample size | Sample Mean |
Sample Standard deviation |
|---|---|---|---|
| 1 | n1 | ˉx1 | s1 |
| 2 | n2 | ˉx2 | s2 |
Throughout this section, the subscripts 1 and 2 show the population to which a parameter or a sample statistic refers.
The two-sample t statistic
The natural estimator of the difference μ1−μ2 is the difference between the sample means, ˉx1−ˉx2. If we are to base inference on this statistic, we must know its sampling distribution. Here are some facts:
- The mean of the difference ˉx1−ˉx2 is the difference of the means μ1−μ2. This follows from the addition rule for means and the fact that the mean of any ˉx is the same as the mean μ of the population.
The variance of the difference ˉx1−ˉx2 is
σ21n1+σ22n2
Because the samples are independent, their sample means ˉx1 and ˉx2 are independent random variables. The addition rule for variances says that the variance of the difference of two independent random variables is the sum of their variances.
- If the two population distributions are both Normal, then the distribution of ˉx1−ˉx2 is also Normal. This is true because each sample mean alone is Normally distributed and a difference of Normal random variables is also Normal.
Because any Normal random variable has the N(0, 1) distribution when standardized, we have arrived at a new z statistic. The two-sample z statistic
z=(ˉx1−ˉx2)−(μ1−μ2)√σ21n1+σ22n2
has the standard Normal N(0, 1) sampling distribution and would be used in inference when the two population standard deviations σ1 and σ2 are known.
In practice, however, σ1 and σ2 are not known. We estimate them by the sample standard deviations s1 and s2 from our two samples. Following the pattern of the one-sample case, we substitute the standard errors for the standard deviations in the two-sample z statistic. The result is the two-sample t statistic:
t=(ˉx1−ˉx2)−(μ1−μ2)√s21n1+s22n2
two-sample t statistic
Unfortunately, this statistic does not have a t distribution. A t distribution replaces an N(0, 1) distribution only when a single standard deviation (σ) is replaced by an estimate (s). In this case, we replaced two standard deviations (σ1 and σ2) by their estimates (s1 and s2).
Nonetheless, we can approximate the distribution of the two-sample t statistic by using the t(k) distribution with an approximation for the degrees of freedom k. We use these approximations to find approximate values of t* for confidence intervalsand to find approximate P-values for significance tests. There are two procedures used in practice:
df approximation
- Use an approximation known as the Satterthwaite approximation to calculate a value of k from the data. In general, this k will not be an integer.
- Use degrees of freedom k equal to the smaller of n1−1 and n2−1.
Satterthwaite
approximation
The choice of approximation rarely makes a difference in our conclusion. Most statistical software uses the first option to approximate the t(k) distribution unless the user requests another method. Use of this approximation without software is a bit complicated.18
If you are not using software, we recommend the second approximation. This approximation is appealing because it is conservative.19 That is, margins of error for confidence intervals are a bit wider than they need to be, so the true confidence level is larger than C. For significance testing, the true P-values are a bit smaller than those we obtain from the approximation; thus, for tests at a fixed significance level, we are a little less likely to reject H0 when it is true.
The two-sample t confidence interval
We now apply the basic ideas about t procedures to the problem of comparing two means when the standard deviations are unknown. We start with confidence intervals.
Two-Sample t Confidence Interval
Draw an SRS of size n1 from a Normal population with unknown mean μ1 and an independent SRS of size n2 from another Normal population with unknown mean μ2. The confidence interval for μ1−μ2 given by
(ˉx1−ˉx2)±t*√s21n1+s22n2
has confidence level at least C no matter what the population standard deviations may be. The margin of error is
t*√s21n1+s22n2
Here, t* is the value for the t(k) density curve with area C between −t* and t*. The value of the degrees of freedom k is approximated by software or the smaller of n1−1 and n2−1.
EXAMPLE 7.10 Smart Shopping Carts and Spending
smrtcrt
Smart shopping carts are shopping carts equipped with scanners that track the total price of the items in the cart. While both consumers and retailers have expressed interest in the use of this technology, actual implementation has been slow. One reason for this is uncertainty in how real-time spending feedback affects shopping. Retailers do not want to adopt a technology that is going to lower sales.
To help understand the smart shopping cart’s influence on spending behavior, a group of researchers designed a study to compare spending with and without realtime feedback. Each participant was asked to shop at an online grocery store for items on a common grocery list. The goal was to keep spending around a budget of $35. Half the participants were randomly assigned to receive real-time feedback—specifically, the names of the products currently in their cart and the total price. The non-feedback participants only saw the total price when they completed their shopping.
Figure 7.9 shows side-by-side boxplots of the data.20 There appears to be a slight skewness in the total price, but no obvious outliers in either group. Given these results and the large sample sizes, we feel confident in using the t procedures.
In general, the participants with real-time feedback appear to have spent more than those without feedback. The summary statistics are
| Group | n | ˉx | s |
|---|---|---|---|
| With feedback | 49 | 33.137 | 6.568 |
| Without feedback | 48 | 30.315 | 6.846 |
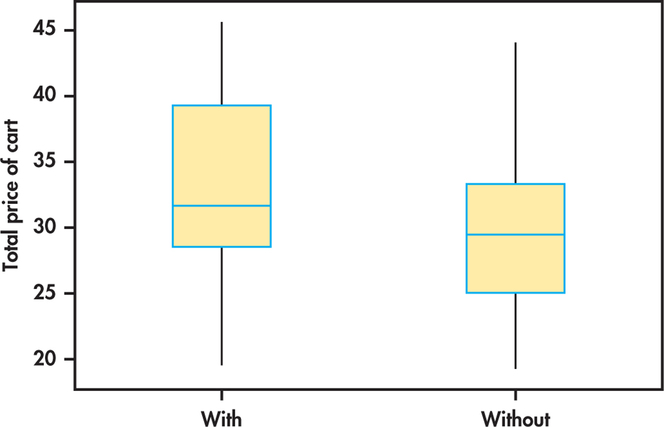
We’d like to estimate the difference in the two means and provide an estimate of the precision. Plugging in these summary statistics, the 95% confidence interval for the difference in means is
(ˉx1−ˉx2)±t*√s21n1+s22n2=(33.137−30.315)±t*√6.568249+6.846248=2.822±(t*×1.363)
Using software, the degrees of freedom are 94.63 and t*=1.985. This approximation gives
2.822±(1.985×1.363)=2.822±2.706=(0.12, 5.53)
The conservative approach would use the smaller of
n1−1=49−1=48 and n2−1=48−1=47
Table D does not supply a row for t(47) but gives t*=2.021 for t(40). We use k=40 because it is the closest value of k in the table that is less than 47. With this approximation we have
2.822±(2.021×1.363)=2.822±2.755=(0.07, 5.58)
| df=40 | ||
|---|---|---|
| t* | 1.684 | 2.021 |
| C | 90% | 95% |
The conservative approach does give a wider interval than the more accurate approximation used by software. However, the difference is very small (just a nickel at each end). We estimate the mean difference in spending to be $2.82 with a margin of error of slightly more than $2.70. The data do not provide a very precise estimate of this difference.
Apply Your Knowledge
Question 7.40
7.40 How to assemble a new machine.
You ran a two-sample study to compare two sets of instructions on how to assemble a new machine. You randomly assign each employee to one of the instructions and measure the time (in minutes) it takes to assemble. Assume that ˉx1=110, ˉx2=120, s1=8, s2=12, n1=20, and n2=20. Find a 95% confidence interval for the average difference in time using the second approximation for degrees of freedom.
Question 7.41
7.41 Another two-sample t confidence interval.
Refer to the previous exercise. Suppose instead your study results were ˉx1=110, ˉx2=120, s1=8, s2=12, n1=10, and n2=10. Find a 95% confidence interval for the average difference using the second approximation for degrees of freedom. Compare this interval with the one in the previous exercise.
7.41
(−20.32, 0.32). With the smaller sample sizes, the interval got wider.
The two-sample t significance test
The same ideas that we used for the two-sample t confidence intervals also apply to two-sample t significance tests. We can use either software or the conservative approach with Table D to approximate the P-value.
Two-Sample t Significance Test
Draw an SRS of size n1 from a Normal population with unknown mean μ1 and an independent SRS of size n2 from another Normal population with unknown mean μ1. To test the hypothesis H0:μ1=μ2, compute the two-sample t statistic
t=(ˉx1−ˉx2)−(μ1−μ2)√s21n1+s22n2
and use P-values or critical values for the t(k) distribution, where the degrees of freedom k are either approximated by software or are the smaller of n1−1 and n2−1.
EXAMPLE 7.11 Does Real-time Feedback Influence Spending?
smrtcrt
For the grocery spending study described in Example 7.10, we want to see if there is a difference in average spending between the group of participants that had real-time feedback and the group that did not. For a formal significance test, the hypotheses are
H0:μ1=μ2Ha:μ1≠μ2
The two-sample t test statistic is
t=(ˉx1−ˉx2)−0√s21n1+s22n2=33.137−30.315√6.568249+6.846248=2.07
The P-value for the two-sided test is 2P(T≥2.07). Software gives the approximate P-value as 0.0410 and uses 94.63 as the degrees of freedom.
For the second approximation, the degrees of freedom k are equal to 47. Because there is no row for k=47, we use the closest value of k in the table that is less than 47. Comparing t=2.07 with the entries in Table D for 40 degrees of freedom, we see that P lies between 2(0.02)=0.04 and 2(0.025)=0.05. The data do suggest that consumers on a budget will spend more when provided with real-time feedback (t=2.07, df=40, 0.04<P<0.05).
| df=40 | ||
|---|---|---|
| p | 0.025 | 0.02 |
| t* | 2.021 | 2.123 |
Apply Your Knowledge
Question 7.42
7.42 How to assemble a new machine, continued.
Refer to Exercise 7.40 (page 382). Perform a significance test to see if there is a difference between the two sets of instructions using α=0.05. Make sure to specify the hypotheses, test statistic, and its P-value, and state your conclusion.
Question 7.43
7.43 Another two-sample t-test.
Refer to Exercise 7.41 (page 382).
- Perform a significance test to see if there is a difference between the two sets of instructions using α=0.05.
- Describe how you could use the 95% confidence interval you calculated in Exercise 7.41 to determine if the there is a difference between the two sets of instructions at significance level 0.05.
7.43
(a) H0:μ1=μ2. Ha:μ1≠μ2. (b) df=9, 0.05<P-value<0.10 t=−2.19. df=9, 0.05<P-value<0.10. The data are not significant at the 5% level, and there is not enough evidence to show a difference between the two sets of instructions. (b) Because the confidence interval contains 0, we fail to reject H0.
Robustness of the two-sample procedures
The two-sample t procedures are more robust than the one-sample t methods. When the sizes of the two samples are equal and the distributions of the two populations being compared have similar shapes, probability values from the t table are quite accurate for a broad range of distributions when the sample sizes are as small as n1=n2=5.21 When the two population distributions have different shapes, larger samples are needed. The guidelines given on page 372 for the use of one-sample t procedures can be adapted to two-sample procedures by replacing “sample size” with the “sum of the sample sizes” n1+n2. Specifically,
- If n1+n2 is less than 15: Use t procedures if the data are close to Normal. If the data in either sample are clearly non-Normal or if outliers are present, do not use t.
- If n1+n2 is at least 15 and less than 40: The t procedures can be used except in the presence of outliers or strong skewness.
- Large samples: The t procedures can be used even for clearly skewed distributions when the sample is large, roughly n1+n2≥40.
These guidelines are rather conservative, especially when the two samples are of equal size. In planning a two-sample study, you should usually choose equal sample sizes. The two-sample t procedures are most robust against non-Normality in this case, and the conservative probability values are most accurate.
Here is an example with large sample sizes that are almost equal. Even if the distributions are not Normal, we are confident that the sample means will be approximately Normal. The two-sample t procedures are very robust in this case.
EXAMPLE 7.12 Wheat Prices
The U.S. Department of Agriculture (USDA) uses sample surveys to produce important economic estimates.22 One pilot study estimated wheat prices in July and in January using independent samples of wheat producers in the two months. Here are the summary statistics, in dollars per bushel:
| Month | n | ˉx | s |
|---|---|---|---|
| January | 45 | $6.66 | $0.24 |
| July | 50 | $6.93 | $0.27 |
The July prices are higher on the average. But we have data from only a limited number of producers each month. Can we conclude that national average prices in July and January are not the same? Or are these differences merely what we would expect to see due to random variation?
Because we did not specify a direction for the difference before looking at the data, we choose a two-sided alternative. The hypotheses are
H0:μ1=μ2Ha:μ1≠μ2
Because the samples are moderately large, we can confidently use the t procedures even though we lack the detailed data and so cannot verify the Normality condition.
The two-sample t statistic is
t=(ˉx1−ˉx2)−0√s21n1+s22n2=6.93−6.66√0.27250+0.24245=5.16
The conservative approach finds the P-value by comparing 5.16 to critical values for the t(44) distribution because the smaller sample has 45 observations. We must double the table tail area p because the alternative is two-sided.
| df=40 | ||
|---|---|---|
| p | 0.0005 | |
| t* | 3.551 | |
Table D does not have entries for 44 degrees of freedom. When this happens, we use the next smaller degrees of freedom. Our calculated value of t is larger than the p=0.0005 entry in the table. Doubling 0.0005, we conclude that the P-value is less than 0.001. The data give conclusive evidence that the mean wheat prices were higher in July than they were January (t=5.16, df=44,p<0.001).
In this example, the exact P-value is very small because t=5.13 says that the observed mean is more than five standard deviations above the hypothesized mean. The difference in mean prices is not only highly significant but large enough (27 cents per bushel) to be important to producers.
In this and other examples, we can choose which population to label 1 and which to label 2. After inspecting the data, we chose July as Population 1 because this choice makes the t statistic a positive number. This avoids any possible confusion from reporting a negative value for t. Choosing the population labels is not the same as choosing a one-sided alternative after looking at the data. Choosing hypotheses after seeing a result in the data is a violation of sound statistical practice.
Inference for small samples
Small samples require special care. We do not have enough observations to examine the distribution shapes, and only extreme outliers stand out. The power of significance tests tends to be low, and the margins of error of confidence intervals tend to be large. Despite these difficulties, we can often draw important conclusions from studies with small sample sizes. If the size of an effect is as large as it was in the preceding wheat price example, it should still be evident even if the n’s are small.
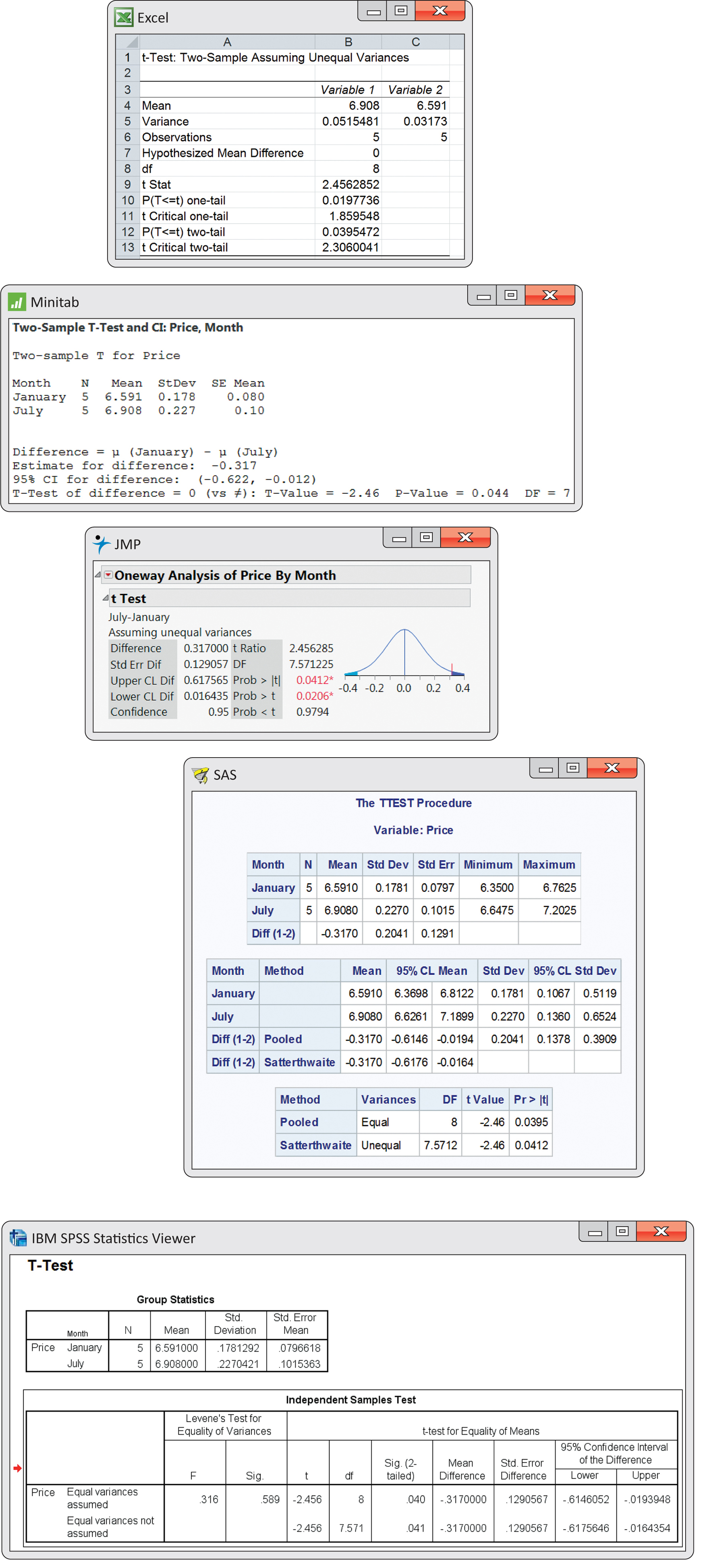
EXAMPLE 7.13 More about Wheat Prices
wheat
In the setting of Example 7.12, a quick survey collects prices from only five producers each month. The data are
| Month | Price ($/bushel) | ||||
|---|---|---|---|---|---|
| January | 6.6125 | 6.4775 | 6.3500 | 6.7525 | 6.7625 |
| July | 6.7350 | 6.9000 | 6.6475 | 7.2025 | 7.0550 |
The prices are reported to the nearest quarter of a cent. First, examine the distributions with a back-to-back stemplot after rounding each price to the nearest cent.
| January | July | |
| 5 | 6.3 | |
| 8 | 6.4 | |
| 6.5 | ||
| 1 | 6.6 | 5 |
| 65 | 6.7 | 4 |
| 6.8 | ||
| 6.9 | 0 | |
| 7.0 | 6 | |
| 7.1 | ||
| 7.2 | 0 |
The pattern is reasonably clear. Although there is variation among prices within each month, the top three prices are all from July and the three lowest prices are from January.
A significance test can confirm that the difference between months is too large to easily arise just by chance. We test
H0:μ1=μ2Ha:μ1≠μ2
The price is higher in July (t=2.46, df=7.57, P=0.0412). The difference in sample means is 31.7 cents.
Figure 7.10 gives outputs for this analysis from several software systems. Although the formats and labels differ, the basic information is the same. All report the sample sizes, the sample means and standard deviations (or variances), the t statistic, and its P-value. All agree that the P-value is very small, though some give more detail than others. Excel and JMP outputs, for example, provide both one-sided and two-sided P-values. Some software (SAS, SPSS, and Minitab) labels the groups in alphabetical order. In this example, January is then the first population and t=−2.46, the negative of our result. Always check the means first and report the statistic (you may need to change the sign) in an appropriate way. Be sure to also mention the size of the effect you observed, such as “The sample mean price for July was 31.7 cents higher than in January.”
SAS and SPSS report the results of two t procedures: a special procedure that assumes that the two population variances are equal and the general two-sample procedure that we have just studied. This “equal-variances” procedure is most helpful when the sample sizes n1 and n2 are small and it is reasonable to assume equal variances.
The pooled two-sample t procedures
There is one situation in which a t statistic for comparing two means is not approximately t distributed but has exactly a t distribution. Suppose that the two Normal population distributions have the same standard deviation. In this case, we need substitute only a single standard error in a z statistic, and the resulting t statistic has a t distribution. We will develop the z statistic first, as usual, and from it the t statistic.
Call the common—but still unknown—standard deviation of both populations σ. Both sample variances s21 and s22 estimate σ2. The best way to combine these two estimates is to average them with weights equal to their degrees of freedom. This gives more weight to the information from the larger sample. The resulting estimator of σ2 is
s2P=(n2−1)s21+(n2−1)s22n1+n2−2
This is called the pooled estimator of σ2 because it combines the information in both samples.
pooled estimator of σ2
When both populations have variance σ2, the addition rule for variances says that ˉx1−ˉx2 has variance equal to the sum of the individual variances, which is
σ2n1+σ2n2=σ2(1n1+1n2)
The standardized difference of means in this equal-variance case is, therefore,
z=(ˉx1−ˉx2)−(μ1−μ2)σ√1n1+1n2
This is a special two-sample z statistic for the case in which the populations have the same σ. Replacing the unknown σ by the estimate sp gives a t statistic. The degrees of freedom are n1+n2−2, the sum of the degrees of freedom of the two sample variances. This statistic is the basis of the pooled two-sample t inference procedures.
Pooled Two-Sample t Procedures
Draw an SRS of size n1 from a Normal population with unknown mean μ1 and an independent SRS of size n2 from another Normal population with unknown mean μ2. Suppose that the two populations have the same unknown standard deviation. A level C confidence interval for μ1−μ2 is
(ˉx1−ˉx2)±t*sp√1n1+1n2
Here t* is the value for the t(n1+n2−2) density curve with area C between −t* and t*.
To test the hypothesis H0:μ1=μ2, compute the pooled two-sample t statistic
t=ˉx1−ˉx2sp√1n1+1n2
and use P-values from the t(n1+n2−2) distribution.

CASE 7.2 Active versus Failed Retail Companies
In what ways are companies that fail different from those that continue to do business? To answer this question, one study compared various characteristics of active and failed retail firms.23 One of the variables was the cash flow margin. Roughly speaking, this is a measure of how efficiently a company converts its sales dollars to cash and is a key profitability measure. The higher the percent, the more profitable the company. The data for 101 companies appear in Table 7.3.
| Active firms | Failed firms | |||||||
|---|---|---|---|---|---|---|---|---|
| −15.57 | 4.13 | −19.37 | 17.27 | 32.29 | −1.44 | 23.87 | 49.07 | −7.53 |
| 23.43 | −8.75 | −1.35 | 34.55 | 1.70 | −0.67 | −23.91 | 7.29 | −14.81 |
| 3.17 | 11.62 | 9.38 | 13.40 | 2.20 | −22.26 | −5.12 | −24.34 | −38.27 |
| −0.35 | −27.78 | 0.65 | −40.82 | 23.55 | 24.45 | 7.71 | −28.79 | −38.35 |
| −9.65 | −16.01 | 36.31 | −27.71 | 9.73 | 40.48 | 9.88 | −7.99 | −18.91 |
| 3.37 | 5.80 | −15.60 | −3.58 | 8.46 | 8.83 | −46.38 | −41.30 | 0.37 |
| 40.25 | −13.39 | 15.86 | −2.25 | 12.97 | 28.21 | 1.41 | −25.56 | 5.28 |
| 11.02 | 30.00 | 4.84 | 30.60 | 6.57 | −20.31 | −15.13 | 8.48 | 15.72 |
| 27.97 | 3.72 | −0.71 | −16.46 | 7.76 | −4.20 | −11.00 | 1.27 | 14.23 |
| 13.08 | −9.31 | 20.21 | −10.45 | 21.39 | ||||
| −22.10 | −24.55 | 28.93 | 35.83 | 21.02 | ||||
| 12.28 | 0.43 | 22.49 | −8.54 | −30.46 | ||||
| −1.89 | 27.92 | 32.79 | −0.52 | 6.35 | ||||

As usual, we first examine the data. Histograms for the two groups of firms are given in Figure 7.11. Normal curves with mean and standard deviation equal to the sample values are superimposed on the histograms. The distribution for the active firms looks more Normal than the distribution for the failed firms. However, there are no outliers or strong departures from Normality that will prevent us from using the t procedures for these data. Let’s compare the mean cash flow margin for the two groups of firms using a significance test.
EXAMPLE 7.14 Does the Cash Flow Margin Differ?
cmps
CASE 7.2 Take Group 1 to be the firms that were active and Group 2 to be those that failed. The question of interest is whether or not the mean cash flow margin is different for the two groups. We therefore test
H0:μ1=μ2Ha:μ1≠μ2
Here are the summary statistics:
| Group | Firms | n | ˉx | s |
|---|---|---|---|---|
| 1 | Active | 74 | 5.42 | 18.80 |
| 2 | Failed | 27 | −7.14 | 21.67 |
The sample standard deviations are fairly close. A difference this large is not particularly unusual even in samples this large. We are willing to assume equal population standard deviations. The pooled sample variance is
s2p=(n1−1)s21+(n2−1)s22n1+n2−2=(73)(18.80)2+(26)(21.67)274+27−2=383.94
so that
sp=√383.94=19.59
The pooled two-sample t statistic is
t=ˉx1-ˉx2sp√1n1+1n2=5.42-(-7.14)19.59√174+127=2.85
The P-value is P(T≥2.85), where T has the t(99) distribution.
In Table D, we have entries for 80 and 100 degrees of freedom. We will use the entries for 100 because k=99 is so close. Our calculated value of t is between the p=0.005 and p=0.0025 entries in the table. Doubling these, we conclude that the two-sided P-value is between 0.005 and 0.01. Statistical software gives the result p=0.005. There is strong evidence that the average cash flow margins are different.
| df=100 | ||
|---|---|---|
| p | 0.005 | 0.0025 |
| t* | 2.626 | 2.871 |
Of course, a P-value is rarely a complete summary of a statistical analysis. To make a judgment regarding the size of the difference between the two groups of firms, we need a confidence interval.
EXAMPLE 7.15 How Different Are Cash Flow Margins?
cmps
CASE 7.2 The difference in mean cash flow margins for active versus failed firms is
ˉx1−ˉx2=5.42−(−7.14)=12.56
For a 95% margin of error, we will use the critical value t*=1.984 from the t(100) distribution. The margin of error is
t*sp√1n1+1n2=(1.984)(19.59)√174+127=8.74
We report that the active firms have current cash flow margins that average 12.56% higher than failed firms, with margin of error 8.74% for 95% confidence. Alternatively, we are 95% confident that the difference is between 3.82% and 21.30%.
| df=100 | ||
|---|---|---|
| t* | 1.660 | 1.984 |
| C | 90% | 95% |
The pooled two-sample t procedures are anchored in statistical theory and have long been the standard version of the two-sample t in textbooks. But they require the condition that the two unknown population standard deviations are equal. This condition is hard to verify. We discuss methods to assess this condition in Chapter 14.
The pooled t procedures are, therefore, a bit risky. They are reasonably robust against both non-Normality and unequal standard deviations when the sample sizes are nearly the same. When the samples are quite different in size, the pooled t procedures become sensitive to unequal standard deviations and should be used with caution unless the samples are large. Unequal standard deviations are quite common. In particular, it is common for the spread of data to increase when the center moves up. We recommend regular use of the unpooled t procedures, particularly when software automates the Satterthwaite approximation.
Apply Your Knowledge
Question 7.44
7.44 Using software.
Figure 7.10 (pages 387–388) gives the outputs from five software systems for comparing prices received by wheat producers in July and January for small samples of five producers in each month. Some of the software reports both pooled and unpooled analyses. Which outputs give the pooled results? What is the pooled t test statistic and its P-value?
Question 7.45
7.45 Wheat prices revisited.
Example 7.12 (pages 384–385) gives summary statistics for the price of wheat in January and July. The two sample standard deviations are relatively close, so we may be willing to assume equal population standard deviations. Calculate the pooled t test statistic and its degrees of freedom from the summary statistics. Use Table D to assess significance. How do your results compare with the unpooled analysis in the example?
7.45
t=−5.13. df=93. P-value<0.001. The data give evidence that there is a difference between the January and July wheat prices. The results are nearly identical to the unpooled analysis.
