8.1 Inference for a Single Proportion
 This page includes Video Technology Manuals
This page includes Video Technology Manuals This page includes Statistical Videos
This page includes Statistical Videos

A Pew survey asked a panel of experts whether or not they thought that networked, automated, artificial intelligence (AI), and robotic devices will have displaced more jobs than they have created (net jobs) by 2025.2 A total of 1896 experts responded to this question. In this sample 48% were concerned that this displacement was a real possibility.
For problems involving a single proportion, we will use n for the sample size and X for the count of the outcome of interest. Often, we will use the terms “success” and “failure” for the two possible outcomes. When we do this, X is the number of successes.
EXAMPLE 8.1 Data for Robotics and Jobs
CASE 8.1 The sample size is the number of experts who responded to the Pew survey question, n=1896. The report on the survey tells us that 48% of the respondents believe net jobs will decrease by 2025 due to networked, automated, artificial intelligence (AI), and robotic devices. Thus, the sample proportion is ˆp=0.48. We can calculate the count X from the information given; it is the sample size times the proportion responding Yes, X=nˆp=1896(0.48)=910.
We would like to know the proportion of experts who would respond Yes to the question about net jobs loss. This population proportion is the parameter of interest. The statistic used to estimate this unknown parameter is the sample proportion. The sample proportion is ˆp=X/n.
population proportion
sample proportion
EXAMPLE 8.2 Estimating the Proportion of Experts Who Think That Net Jobs Will decrease
CASE 8.1 The sample proportion ˆp in Case 8.1 is a discrete random variable that can take the values 0, 1/1896, 2/1896, . . . , 1895/1896, or 1. For our particular sample, we have
ˆp=9101896=0.48
In many cases, a probability model for ˆp can be based on the binomial distributions for counts. In Chapter 5, we described this situation as the binomial setting. If the sample size n is very small, we can base tests and confidence intervals for p on the discrete distribution of ˆp. We will focus on situations where the sample size is sufficiently large that we can approximate the distribution of ˆp by a Normal distribution.
Sampling Distribution of a Sample Proportion
Choose an SRS of size n from a large population that contains population proportion p of “successes.” Let X be the count of successes in the sample, and let ˆp be the sample proportion of successes,
ˆp=Xn
Then:
- For large sample sizes, the distribution of ˆp is approximately Normal.
- The mean of the distribution of ˆp is p.
- The standard deviation of ˆp is
√p(1-p)n
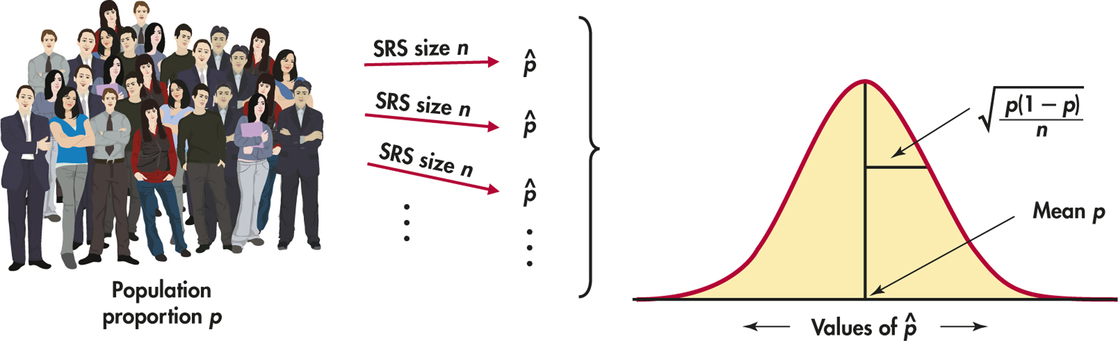
Figure 8.1 summarizes these facts in a form that recalls the idea of sampling distributions. Our inference procedures are based on this Normal approximation. These procedures are similar to those for inference about the mean of a Normal distribution (page 42). We will see, however, that there are a few extra details involved, caused by the added difficulty in approximating the discrete distribution of ˆp by a continuous Normal distribution.
Apply Your Knowledge
Question 8.1
8.1 Community banks.
The American Bankers Association Community Bank Insurance Survey for 2013 had responses from 151 banks. Of these, 80 were Community Banks, defined to be banks with assets of $1 billion or less.3
- What is the sample size n for this survey?
- What is the count X? Describe the count in a short sentence.
- Find the sample proportion ˆp.
8.1
(a) n=151. (b) X=80, it is the count of banks with assets of $1 billion or less. (c) ˆp=0.5298.
Question 8.2
8.2 Coca-Cola and demographics
A Pew survey interviewed 162 CEOs from U.S. companies. The report of the survey quotes Muhtar Kent, Coca-Cola Company chairman and CEO, on the importance of demographics in developing customer strategies. Kent notes that the population of the United States is aging and that there is a need to provide products that appeal to this segment of the market. The survey found that 52% of the CEOs in the sample are planning to change their customer growth and retention strategies.
- How many CEOs participated in the survey? What is the sample size n for the survey?
- What is the count X of those who said that they are planning to change their customer growth and retention strategies?
- Find the sample proportion ˆp.
- The quotes from Muhtar Kent in the report could be viewed as anecdotal data. Do you think that these quotes are useful to explain and interpret the results of the survey? Write a short paragraph discussing your answer.
Large-sample confidence interval for a single proportion
The sample proportion ˆp=X/n is the natural estimator of the population proportion p. Notice that √p(1-p)/n, the standard deviation of ˆp, depends upon the unknown parameter p. In our calculations, we estimate it by replacing the population parameter p with the sample estimate ˆp. Therefore, our estimated standard error is SEˆp=√ˆp(1-ˆp)/n. This quantity is the estimate of the standard deviation of the distribution of ˆp. If the sample size is large, the distribution of ˆp will be approximately Normal with mean p and standard deviation SEˆp. It follows that ˆp will be within two standard deviations (2SEˆp) of the unknown parameter p about 95% of the time. This is how we use the Normal approximation to construct the large-sample confidence interval for p. Here are the details.
Confidence Interval for a Population Proportion
Choose an SRS of size n from a large population with unknown proportion p of successes. The sample proportion is
ˆp=Xn
The standard error of ˆp is
SEˆp=√ˆp(1-ˆp)n
and the margin of error for confidence level C is
m=z*SEˆp
where z* is the value for the standard Normal density curve with area C between −z* and z*. The large-sample level C confidence interval for p is
ˆp±m
You can use this interval for 90% (z*=1.645),95% (z*=1.960), or 99% (z*=2.576) confidence when the number of successes and the number of failures are both at least 10.
EXAMPLE 8.3 Confidence Interval for the Proportion of Experts Who Think net Jobs Will Decrease
CASE 8.1 The sample survey in Case 8.1 found that 910 of a sample of 1896 experts reported that they think net jobs will decrease by 2025 because of robots and related technology developments. Thus, the sample size is n=1896 and the count is X=910. The sample proportion is
ˆp=Xn=9101896=0.47996
The standard error is
SEˆp=√ˆp(1-ˆp)n=√0.47996(1-0.47996)1896=0.011474
The z critical value for 95% confidence is z*=1.96, so the margin of error is
m=1.96SEˆp=(1.96)(0.011474)=0.022488
The confidence interval is
ˆp±m=0.480±0.022
We are 95% confident that between 45.8% and 50.2% of experts would report that they think net jobs will decrease by 2025 because of robots and related technology developments.

In performing these calculations, we have kept a large number of digits for our intermediate calculations. However, when reporting the results, we prefer to use rounded values. For example, “48.0% with a margin of error of 2.2%.” You should always focus on what is important. Reporting extra digits that are not needed can divert attention from the main point of your summary. There is no additional information to be gained by reporting ˆp=0.47996 with a margin of error of 0.022488. Do you think it would be better to report 48% with a 2% margin of error?

Remember that the margin of error in any confidence interval includes only random sampling error. If people do not respond honestly to the questions asked, for example, your estimate is likely to miss by more than the margin of error. Similarly, response bias can also be present.
Because the calculations for statistical inference for a single proportion are relatively straightforward, we often do them with a calculator or in a spreadsheet. Figure 8.2 gives output from JMP and Minitab for the data in Case 8.1. There are alternatives to the Normal approximations that we have presented that are used by some software packages. Minitab uses one of these, called the exact method, as a default but provides options for selecting different methods. In general, the alternatives give very similar results, particularly for large sample sizes.
As usual, the outputs report more digits than are useful. When you use software, be sure to think about how many digits are meaningful for your purposes. Do not clutter your report with information that is not meaningful.
Apply Your Knowledge
Question 8.3
8.3 Community banks
Refer to Exercise 8.1 (page 419).
- Find SEˆp, the standard error of ˆp. Explain the meaning of the standard error in simple terms.
- Give the 95% confidence interval for p in the form of estimate plus or minus the margin of error.
- Give the confidence interval as an interval of percents.
8.3
(a) SEˆp=0.0406. This tells us how much ˆp varies. (b) 0.5298±0.0796. (c) (45.0%, 60.9%).
Question 8.4
8.4 Customer growth and retention strategy
Refer to Exercise 8.2 (page 419).
- Find SEˆp, the standard error of ˆp.
- Give the 95% confidence interval for p in the form of estimate plus or minus the margin of error.
- Give the confidence interval as an interval of percents.
Plus four confidence interval for a single proportion
Suppose we have a sample where the count is X=0. Then, because ˆp=0, the standard error and the margin of error based on this estimate will both be 0. The confidence interval for any confidence level would be the single point 0. Confidence intervals based on the large-sample Normal approximation do not make sense in this situation.
Both computer studies and careful mathematics show that we can do better by moving the sample proportion ˆp away from 0 and 1.4 There are several ways to do this. Here is a simple adjustment that works very well in practice.
The adjustment is based on the following idea: act as if we have four additional observations, two of which are successes and two of which are failures. The new sample size is n+4 and the count of successes is X+2. Because this estimate was first suggested by Edwin Bidwell Wilson in 1927 (though rarely used in practice until recently), we call it the Wilson estimate.
Wilson estimate
To compute a confidence interval based on the Wilson estimate, first replace the value of X by X+2 and the value of n by n+4. Then use these values in the formulas for the z confidence interval.
In Example 8.1, we had X=910 and n=1896. To apply the “plus four” approach, we use the z procedure with X=912 and n=1900. You can use this interval when the sample size is at least n=10 and the confidence level is 90%, 95%, or 99%.
In general, the large sample interval will agree pretty well with the Wilson estimate when the conditions for the application of the large sample method are met (C equal to 90%, 95%, or 99% and and the number of successes and failures are both at least 10). The Wilson estimates are most useful when these conditions are not met and the sample proportion is close to zero or one.
Apply Your Knowledge
Question 8.5
8.5 Use plus four for net jobs.
Refer to Example 8.3 (pages 420–421). Compute the plus four 95% confidence interval, and compare this interval with the one given in that example.
8.5
(0.4575, 0.5025). This plus-four interval is quite close to the original interval of (0.458, 0.502).
Question 8.6
8.6 New-product sales
Yesterday, your top salesperson called on 12 customers and obtained orders for your new product from all 12. Suppose that it is reasonable to view these 12 customers as a random sample of all of her customers.
- Give the plus four estimate of the proportion of her customers who would buy the new product. Notice that we don't estimate that all customers will buy, even though all 12 in the sample did.
- Give the margin of error and the confidence interval for 95% confidence. (You may see that the upper endpoint of the confidence interval is greater than 1. In that case, take the upper endpoint to be 1.)
- Do the results apply to all your sales force? Explain why or why not.
Question 8.7
8.7 Construct an example
Make up an example where the large-sample method and the plus four method give very different intervals. Do not use a case where either ˆp=0 or ˆp=1.
8.7
Answers will vary. Anything with a very small n and a very high or low X (close to n or 0).
Significance test for a single proportion
We know that the sample proportion ˆp=X/n is approximately Normal, with mean μˆp=p and standard deviation σˆp=√p(1-p)/n. To construct confidence intervals, we need to use an estimate of the standard deviation based on the data because the standard deviation depends upon the unknown parameter p. When performing a significance test, however, the null hypothesis specifies a value for p, which we will call p0. When we calculate P-values, we act as if the hypothesized p were actually true. When we test H0:p=p0, we substitute p0 for p in the expression for σˆp and then standardize ˆp. Here are the details.
z Significance Test for a Population Proportion
Choose an SRS of size n from a large population with unknown proportion p of successes. To test the hypothesis H0:p=p0, compute the z statistic
z=ˆp-p0√p0(1-p0)n
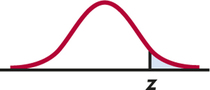
In terms of a standard Normal random variable Z, the approximate P-value for a test of H0 against
Ha:p>p0isP(Z≥z)
Ha:p<p0isP(Z≤z)

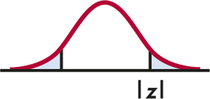
Ha:p≠p0is2P(Z≥|z|)
Use this test when the expected number of successes np0 and the expected number of failures n(1-p0) are both at least 10.
We call this z test a “large-sample test” because it is based on a Normal approximation to the sampling distribution of ˆp that becomes more accurate as the sample size increases. For small samples, or if the population is less than 20 times as large as the sample, consult an expert for other procedures.
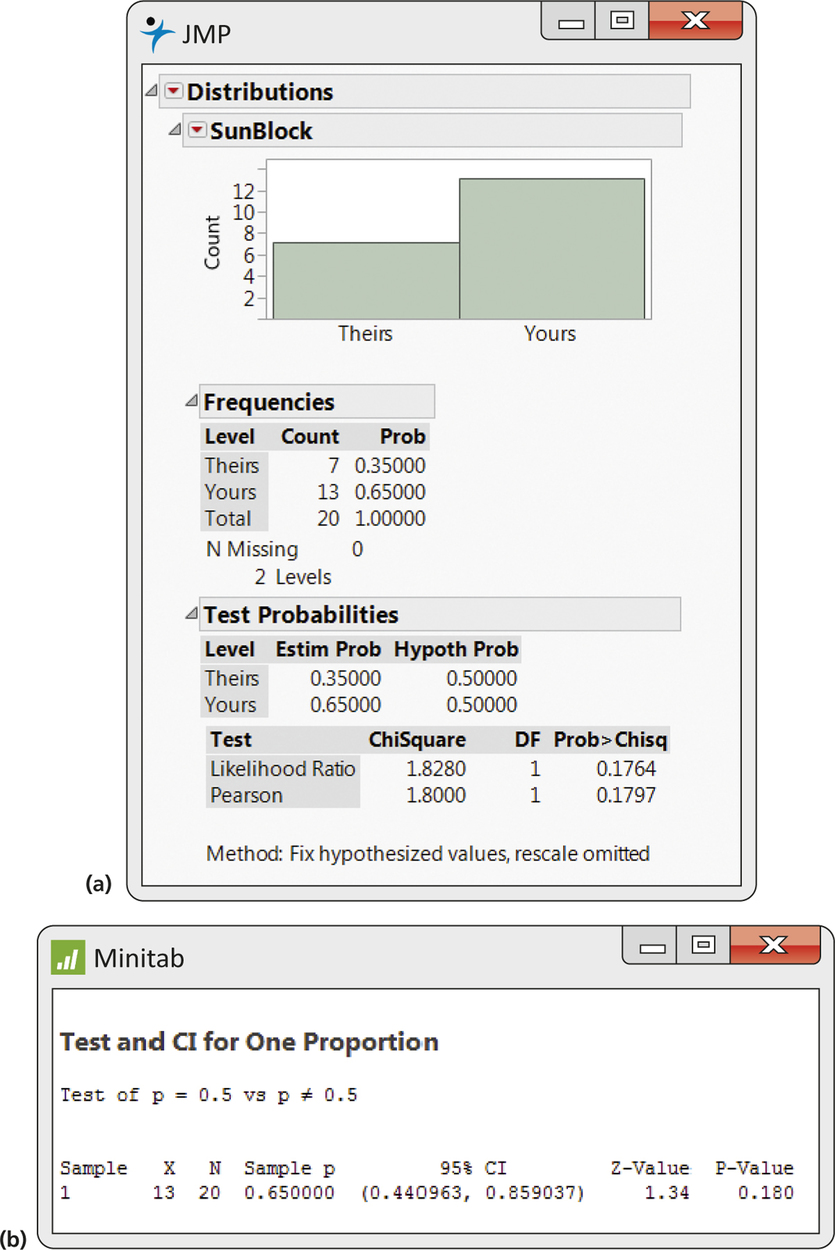
EXAMPLE 8.4 Comparing Two Sunblock Lotions
Your company produces a sunblock lotion designed to protect the skin from both UVA and UVB exposure to the sun. You hire a company to compare your product with the product sold by your major competitor. The testing company exposes skin on the backs of a sample of 20 people to UVA and UVB rays and measures the protection provided by each product. For 13 of the subjects, your product provided better protection, while for the other seven subjects, your competitor's product provided better protection. Do you have evidence to support a commercial claiming that your product provides superior UVA and UVB protection? For the data we have n=20 subjects and X=13 successes. To answer the claim question, we test
H0:p=0.5Ha:p≠0.5
The expected numbers of successes (your product provides better protection) and failures (your competitor's product provides better protection) are 20×0.5=10 and 20×0.5=10. Both are at least 10, so we can use the z test. The sample proportion is
ˆp=Xn=1320=0.65
The test statistic is
z=ˆp-p0√p0(1-p0)n=0.65-0.5√(0.5)(0.5)20=1.34
From Table A, we find P(Z≤1.34)=0.9099, so the probability in the upper tail is 1-0.9099=0.0901. The P-value is the area in both tails, P=2×0.0901=0.1802. JMP and Minitab outputs for the analysis appear in Figure 8.3. Note that JMP uses a different form for the test statistic, but the resulting P-values are essentially the same. We conclude that the sunblock testing data are compatible with the hypothesis of no difference between your product and your competitor's (ˆp=0.65, z=1.34, P=0.18). The data do not provide you with enough evidence to support your advertising claim.
Note that we used a two-sided hypothesis test when we compared the two sunblock lotions in Example 8.4. In settings like this, we must start with the view that either product could be better if we want to prove a claim of superiority. Thinking or hoping that your product is superior cannot be used to justify a one-sided test.
Apply Your Knowledge
Question 8.8
8.8 Draw a picture.
Draw a picture of a standard Normal curve, and shade the tail areas to illustrate the calculation of the P-value for Example 8.4.
Question 8.9
8.9 What does the confidence interval tell us
Inspect the outputs in Figure 8.3, and report the confidence interval for the percent of people who would get better sun protection from your product than from your competitor's. Be sure to convert from proportions to percents and round appropriately. Interpret the confidence interval and compare this way of analyzing data with the significance test.
8.9
(44.1%, 85.9%). With 95% confidence, the percent of people who would get better protection from your product is between 44.1% and 85.9%. The confidence interval gives similar information to the significance test that the percentage is not significantly different than 50% because 50% is inside our interval.
Question 8.10
8.10 The effect of X
In Example 8.4, suppose that your product provided better UVA and UVB protection for 16 of the 20 subjects. Perform the significance test and summarize the results.
Question 8.11
8.11 The effect of n
In Example 8.4, consider what would have happened if you had paid for 40 subjects to be tested. Assume that the results would be the same as what you obtained for 20 subjects; that is, 65% had better UVA and UVB protection with your product.
- Perform the significance test and summarize the results.
- Compare these results with those you found in the previous exercise, and write a short summary of the effect of the sample size on these significance tests.
8.11
(a) ˆp=0.65, Z=1.90, P−value=0.0574. The data do not show a significant difference between your product and your competitor’s. (b) As the sample size increases, the Z test statistic increases and the P-value gets smaller, making the data more significant. So while we didn’t get significance at the 5% level, the data are more significant with the larger sample size.
In Example 8.4, we treated an outcome as a success whenever your product provided better sun protection. Would we get the same results if we defined success as an outcome where your competitor's product was superior? In this setting, the null hypothesis is still H0:p=0.5. You will find that the z test statistic is unchanged except for its sign and that the P-value remains the same.
Apply Your Knowledge
Question 8.12
8.12 Yes or no?
In Example 8.4, we performed a significance test to compare your sunblock with your competitor's. Success was defined as the outcome where your product provided better protection. Now, take the viewpoint of your competitor, and define success as the outcome where your competitor's product provides better protection. In other words, n remains the same (20), but X is now 7.
- Perform the two-sided significance test and report the results. How do these compare with what we found in Example 8.4?
- Find the 95% confidence interval for this setting, and compare it with the interval calculated where success is defined as the outcome when your product provides better protection.
Choosing a sample size for a confidence interval
In Chapter 7, we showed how to choose the sample size n to obtain a confidence interval with specified margin of error m for a Normal mean. Because we are using a Normal approximation for inference about a population proportion, sample size selection proceeds in much the same way.
Recall that the margin of error for the large-sample confidence interval for a population proportion is
m=z*SEˆp=z*√ˆp(1-ˆp)n
Choosing a confidence level C fixes the critical value z*. The margin of error also depends on the value of ˆp and the sample size n. Because we don't know the value of ˆp until we gather the data, we must guess a value to use in the calculations. We will call the guessed value p*. Here are two ways to get p*:
- Use the sample estimate from a pilot study or from similar studies done earlier.
- Use p*=0.5. Because the margin of error is largest when ˆp=0.5, this choice gives a sample size that is somewhat larger than we really need for the confidence level we choose. It is a safe choice no matter what the data later show.
Once we have chosen p* and the margin of error m that we want, we can find the n we need to achieve this margin of error. Here is the result.
Sample Size for Desired Margin of Error
The level C confidence interval for a proportion p will have a margin of error approximately equal to a specified value m when the sample size is
n=(z*m)2p*(1-p*)
Here z* is the critical value for confidence C, and p* is a guessed value for the proportion of successes in the future sample.
The margin of error will be less than or equal to m if p* is chosen to be 0.5. The sample size required is then given by
n=(z*2m)2
The value of n obtained by this method is not particularly sensitive to the choice of p* as long as p* is not too far from 0.5. However, if your actual sample turns out to have ˆp smaller than about 0.3 or larger than about 0.7, the sample size based on p*=0.5 may be much larger than needed.
EXAMPLE 8.5 Planning a Sample of Customers
Your company has received complaints about its customer support service. You intend to hire a consulting company to carry out a sample survey of customers. Before contacting the consultant, you want some idea of the sample size you will have to pay for. One critical question is the degree of satisfaction with your customer service, measured on a 5-point scale. You want to estimate the proportion p of your customers who are satisfied (that is, who choose either “satisfied” or “very satisfied,” the two highest levels on the 5-point scale).
You want to estimate p with 95% confidence and a margin of error less than or equal to 3%, or 0.03. For planning purposes, you are willing to use p*=0.5. To find the sample size required,
n=(z*2m)2=[1.96(2)(0.03)]2=1067.1
Round up to get n=1068. (Always round up. Rounding down would give a margin of error slightly greater than 0.03.)
Similarly, for a 2.5% margin of error, we have (after rounding up)
n=[1.96(2)(0.025)]2=1537
and for a 2% margin of error,
n=[1.96(2)(0.02)]2=2401
News reports frequently describe the results of surveys with sample sizes between 1000 and 1500 and a margin of error of about 3%. These surveys generally use sampling procedures more complicated than simple random sampling, so the calculation of confidence intervals is more involved than what we have studied in this section. The calculations in Example 8.5 nonetheless show, in principle, how such surveys are planned.
In practice, many factors influence the choice of a sample size. Case 8.2 illustrates one set of factors.


An association of Christmas tree growers in Indiana sponsored a sample survey of Indiana households to help improve the marketing of Christmas trees.5 The researchers decided to use a telephone survey and estimated that each telephone interview would take about two minutes. Nine trained students in agribusiness marketing were to make the phone calls between 1:00 P.M. and 8:00 P.M. on a Sunday. After discussing problems related to people not being at home or being unwilling to answer the questions, the survey team proposed a sample size of 500. Several of the questions asked demographic information about the household. The key questions of interest had responses of Yes or No; for example, “Did you have a Christmas tree last year?” The primary purpose of the survey was to estimate various sample proportions for Indiana households. An important issue in designing the survey was, therefore, whether the proposed sample size of n=500 would be adequate to provide the sponsors of the survey with the information they required.
To address this question, we calculate the margins of error of 95% confidence intervals for various values of ˆp.
EXAMPLE 8.6 Margins of Error
CASE 8.2 In the Christmas tree market survey, the margin of error of a 95% confidence interval for any value of ˆp and n=500 is
m=z*SEˆp=1.96√ˆp(1-ˆp)500
The results for various values of ˆp are
| ˆp | m | ˆp | m |
|---|---|---|---|
| 0.05 | 0.019 | 0.60 | 0.043 |
| 0.10 | 0.026 | 0.70 | 0.040 |
| 0.20 | 0.035 | 0.80 | 0.035 |
| 0.30 | 0.040 | 0.90 | 0.026 |
| 0.40 | 0.043 | 0.95 | 0.019 |
| 0.50 | 0.044 |
The survey team judged these margins of error to be acceptable and used a sample size of 500 in their survey.
The table in Example 8.6 illustrates two points. First, the margins of error for ˆp=0.05 and ˆp=0.95 are the same. The margins of error will always be the same for ˆp and 1-ˆp. This is a direct consequence of the form of the confidence interval. Second, the margin of error varies only between 0.040 and 0.044 as ˆp varies from 0.3 to 0.7, and the margin of error is greatest when ˆp=0.5, as we claimed earlier. It is true in general that the margin of error will vary relatively little for values of ˆp between 0.3 and 0.7. Therefore, when planning a study, it is not necessary to have a very precise guess for p. If p*=0.5 is used and the observed ˆp is between 0.3 and 0.7, the actual interval will be a little shorter than needed, but the difference will be quite small.
Apply Your Knowledge
Question 8.13
8.13 Is there interest in a new product?
One of your employees has suggested that your company develop a new product. You decide to take a random sample of your customers and ask whether or not there is interest in the new product. The response is on a 1 to 5 scale, with 1 indicating “definitely would not purchase”; 2, “probably would not purchase”; 3, “not sure”; 4, “probably would purchase”; and 5, “definitely would purchase.” For an initial analysis, you will record the responses 1, 2, and 3 as No and 4 and 5 as Yes. What sample size would you use if you wanted the 95% margin of error to be 0.15 or less?
8.13
n=43.
Question 8.14
8.14 More information is needed
Refer to the previous exercise. Suppose that, after reviewing the results of the previous survey, you proceeded with preliminary development of the product. Now you are at the stage where you need to decide whether or not to make a major investment to produce and market the product. You will use another random sample of your customers, but now you want the margin of error to be smaller. What sample size would you use if you wanted the 95% margin of error to be 0.04 or less?
Choosing a sample size for a significance test
In Chapter 6, we also introduced the idea of power for a significance test. These ideas apply to the significance test for a proportion that we studied in this section. There are some more complicated details, but the basic ideas are the same. Fortunately, software can take care of the details, and we can concentrate on the input and output. To find the required sample size, we need to specify
- the value of p0 in the null hypothesis H0:p=p0
- the alternative hypothesis, two-sided (Ha:p≠p0) one-sided (Ha:p>p0 or Ha:p<p0)
- a value of p for the alternative hypothesis
- the type I error (α, the probability of rejecting the null hypothesis when it is true); usually we choose 5% (α=0.05) for the type I error
- power (probability of rejecting the null hypothesis when it is false); usually we choose 80% (0.80) for power
EXAMPLE 8.7 Sample Size for Comparing Two Sunblock Lotions
In Example 8.4, we performed the significance test for comparing two sunblock lotions in a setting where each subject used the two lotions and the product that provided better protection was recorded. Although your product performed better 13 times in 20 trials, the the value of ˆp=13/20=0.65 was not sufficiently far from the null hypothesized value of p0=0.5 for us to reject the H0,(p=0.18). Let's suppose that the true percent of the time that your lotion would perform better is p0=0.65 and we plan to test the null hypothesis H0:p=0.5 versus the two-sided alternative Ha:p≠0.5 using a type I error probability of 0.05.
What sample size n should we choose if we want to have an 80% chance of rejecting H0? Outputs from JMP and Minitab are given in Figure 8.4. JMP indicates that n=89 should be used, while Minitab suggests n=85. The difference is due to the different methods that can be used for these calculations.
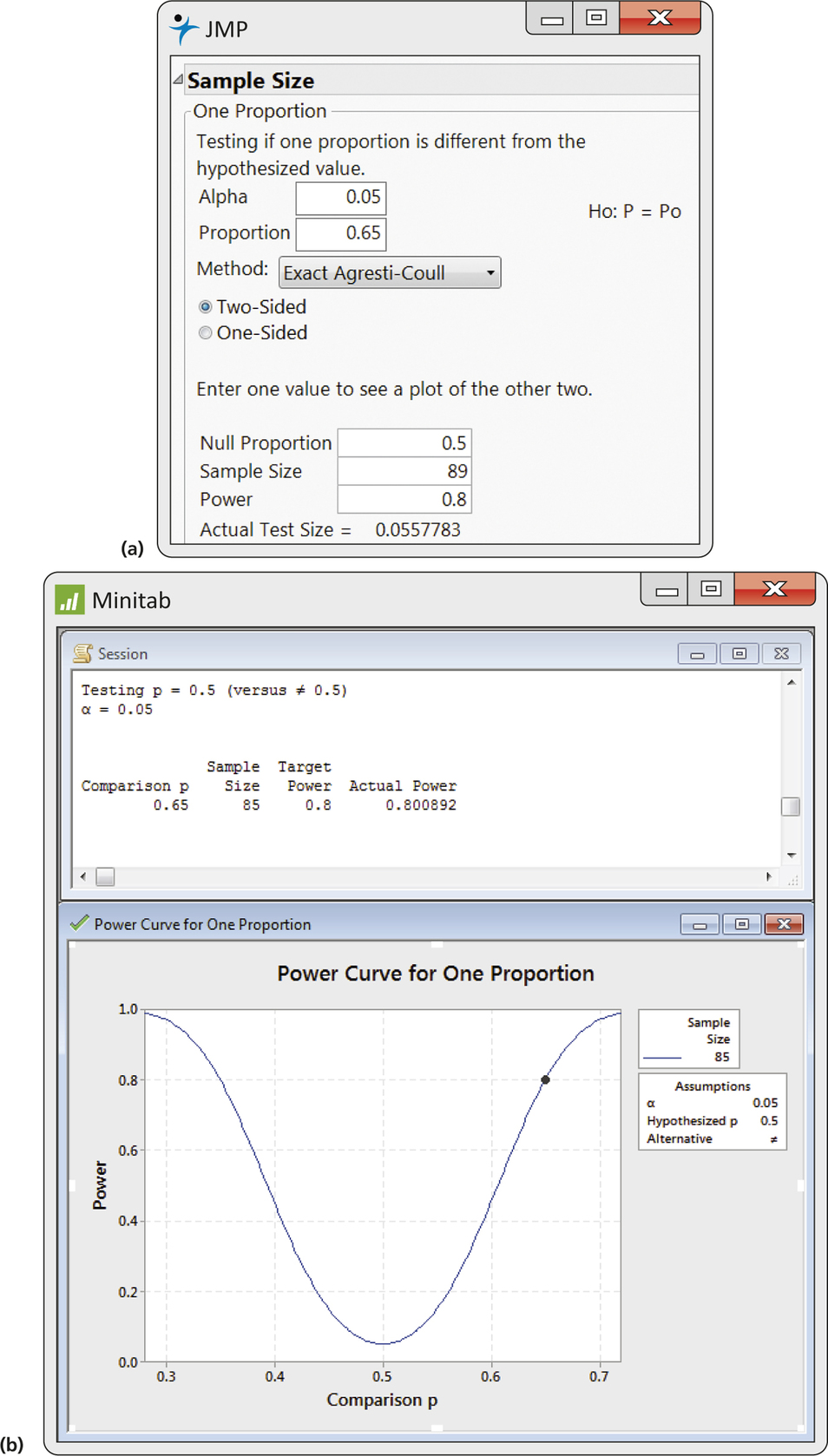
Note that Minitab provides a graph as a function of the value of the proportion for the alternative hypothesis. Similar plots can be produced by JMP. In some situations, you might want to specify the sample size n and have software compute the power. This option is available in JMP, Minitab, and other software.
Apply Your Knowledge
Question 8.15
8.15 Compute the sample size for a different alternative.
Refer to Example 8.7. Use software to find the sample size needed for a two-sided test of the null hypothesis that p=0.5 versus the two-sided alternative with α=0.05 and 80% power if the alternative is p=0.7.
8.15
n=47.
Question 8.16
8.16 Compute the power for a given sample size
Consider the setting in Example 8.7. You have a budget that will allow you to test 100 subjects. Use software to find the power of the test for this value of n.
