Chapter 1. Impact 2.1
Impact …ON TECHNOLOGY: I2.1 Quantum computing
The postulates of quantum mechanics lie at the heart of what might prove one day to be a revolution in the way in which certain calculations are carried out. Quantum mechanics might also undermine one of the most cherished aspects of commerce, war, and government: secrecy. Quantum computing is potentially capable of solving in seconds problems that conventional computing might be unable to solve in the lifetime of the universe.
Conventional digital computing is based on the manipulation of strings of 0s and 1s, or bits (‘binary digits’). Each bit might be realized in practice by the physical state of an object, such as a potential difference across a semiconductor junction or the state of polarization (‘left-circularly polarized’ or ‘right-circularly polarized’) of a photon. We could denote these physical states ψ0 or ψ1. In essence, a conventional digital computer carries out operations on these states. We see in Postulate V (Topic 7), however, that a state in quantum mechanics might be a linear combination of eigenfunctions, such as c0ψ0+ c1ψ1, with arbitrary (or, at least, specified) values of the two coefficients. This superposition of states is called a qubit (for ‘quantum bit’). The core idea of quantum computing is starting to emerge: instead of carrying out operations on certain states of the system individually, computations can be carried out simultaneously on several, and perhaps many, states simultaneously.
The core of conventional computing are various logical circuits such as AND and NOT. Thus, an AND gate gives an output of 1 if both its inputs are 1; a NOT gate gives an output of 0 if the input is 1 and an output of 1 if the input is 0. If we use our photon-polarization model, then if a photon incident on a NOT gate is left-circularly polarized, the output is a photon that is right-circularly polarized, and vice versa. Conventional computers string together these and other so-called Boolean operations and realize them in terms of potential differences at semiconductor junctions.
The Born interpretation of the wavefunction (Topic 5, Postulate II) states that only its square has a direct physical significance. It might then be suspected that, because a quantum computer carries out operations on the wavefunction rather than the probability itself, then the logical circuits will in some sense be acting as the square-root of the usual Boolean operations. That is, instead of NOT acting on the classical bits, the square-root of NOT (denoted √NOT) will be acting on the quantum qubits. Something like that turns out to be the case.
It would take us too far astray to go into the details of quantum logic and its practical implementation (which is still at a primitive stage), but it is worth taking some of the mystery out of √NOT to see that it has a real, physically realizable meaning. To do so, consider the arrangement in Fig. 1a, which shows a photon incident on a half-silvered mirror. If the photon is reflected it enters what we could call the state ψ0 and if it is transmitted it enters what we shall call the state ψ1: the states are physically distinct as the photon occupies different parts of space. However, because we have not made an observation of the location of the photon, there are equal probabilities that it is in either state: according to Postulate V (Topic 7), we have prepared the qubit ψ0 + ψ1 from the state ψ0 (the incident photon was above the mirror). If we were to detect the photon, half the time we would find it above the mirror and half the time below.
Now suppose we join a second similar arrangement to the first, as in Fig. 1b. According to quantum mechanics, the linear combination ψ0 + ψ1 recombines in the second arrangement to result in a photon that emerges below the second half-silvered mirror; that is, in the state ψ1. In other words, the combination of the two arrangements acts as a NOT gate. The implication is that each individual component (as in the first illustration) contributes √NOT, because the succession √NOT√NOT is equivalent to NOT.
Quantum computation is obviously a highly subtle technology, but it is just starting to emerge into practical implementations. It builds conceptually on the postulates of quantum mechanics and will make use of the quantized real systems that we encounter throughout the text.
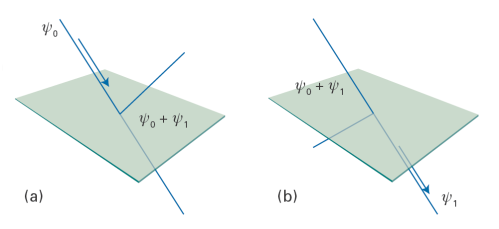
Fig. 1. (a) A photon incident on a half-silvered mirror. If the photon is reflected it enters the state ψ0 and if it is transmitted it enters the state ψ1; the net result is preparation of the state ψ0 + ψ1. (b) When passed through a similar device, the linear combination ψ0 + ψ1 recombines to result in a photon that emerges in the state ψ1. In other words, the combination of the two arrangements acts as a NOT gate.