CHAPTER 14 EXERCISES
Question 14.9
14.9 What number can I be?
(a) What are all the values that a correlation r can possibly take?
(b) What are all the values that a standard deviation s can possibly take?
(c) What are all the values that a mean ˉx can possibly take?
14.9 (a) −1≤ r ≤ 1. (b) s ≥ 0. (c) −∞ ≤ ˉx ≤ ∞ but has to fall within the min and max of a given data set.
Question 14.10
14.10 Measuring mice. For a biology project, you measure the tail length (millimeters) and weight (grams) of 10 mice.
(a) Explain why you expect the correlation between tail length and weight to be positive.
(b) If you measured tail length in centimeters, how would the correlation change?
Question 14.11
 14.11 Living on campus. A February 2, 2008, article in the Columbus Dispatch reported a study on the distances students lived from campus and average GPA. Here is a summary of the results:
14.11 Living on campus. A February 2, 2008, article in the Columbus Dispatch reported a study on the distances students lived from campus and average GPA. Here is a summary of the results:
| Residence | Avg. GPA |
| Residence hall | 3.33 |
| Walking distance | 3.16 |
| Near campus, long walk or short drive |
3.12 |
| Within the county, not near campus |
2.97 |
| Outside the county | 2.94 |
Based on these data, is the association between the distance a student lives from campus and average GPA positive, negative, or near 0?
14.11 Negative.
Question 14.12
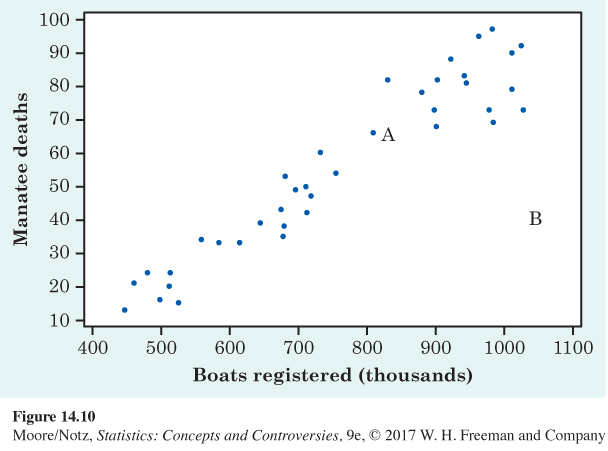
14.12 The endangered manatee. Manatees are large, gentle, slow-moving creatures found along the coast of Florida. Many manatees are injured or killed by boats. Figure 14.10 is a scatterplot of the number of manatee deaths by boats versus the number of boats registered in Florida (in thousands) for the years between 1977 and 2014.
(a) Describe the overall pattern of the relationship in words.
(b) About what are the number of boats registered and manatee deaths for point A?
(c) Suppose there was a point near B. Would this be an outlier? If so, say how it is unusual (for example, “a moderately high number of deaths but a low number of boats registered”).
fig14-10
Question 14.13
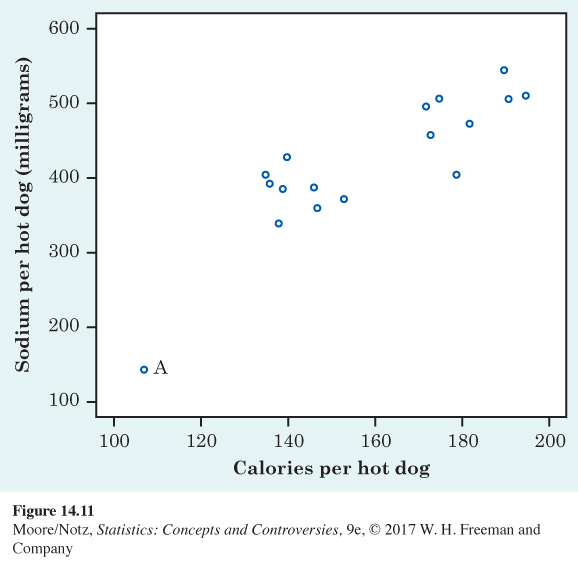
14.13 Calories and salt in hot dogs. Figure 14.11 shows the calories and sodium content in 17 brands of meat hot dogs. Describe the overall pattern of these data. In what way is the point marked A unusual?
14.13 Moderate, roughly linear, and positive. Point A is a hot dog brand that is well below average in both calories and sodium and can be considered an outlier.
Question 14.14
14.14 The endangered manatee. Is the correlation r for the data in Figure 14.10 near −1, clearly negative but not near −1, near 0, clearly positive but not near 1, or near 1? Explain your answer.
Question 14.15
14.15 Calories and salt in hot dogs. Is the correlation r for the data in Figure 14.11 near −1, clearly negative but not near −1, near 0, clearly positive but not near 1, or near 1? Explain your answer.
14.15 This shows a fairly strong positive association, so r should be reasonably close to 1.
Question 14.16
14.16 Comparing correlations. Which of Figure 14.2, 14.10, and 14.11 has a correlation closer to 0? Explain your answer.
Question 14.17
14.17 Outliers and correlation. In Figure 14.11, the point marked A is an outlier. Will removing the outlier increase or decrease r ? Why?
14.17 The correlation decreases when A is removed from Figure 14.11 because that plot looks more linear with A. That is, if we draw a line through that scatterplot, there is a less relative scatter about that line with point A than without.
ex14-18
Question 14.18
14.18 Global warming. Have average global temperatures been increasing in recent years? Here are annual average global temperatures for the last 21 years in degrees Celsius.
(a) Make a scatterplot. (Which is the explanatory variable?)
(b) Is the association between these variables positive or negative? Explain why you expect the relationship to have this direction.
(c) Describe the form and strength of the relationship.
| Year | 1994 | 1995 | 1996 |
| Temperature | 14.23 | 14.35 | 14.22 |
| Year | 1997 | 1998 | 1999 |
| Temperature | 14.42 | 14.54 | 14.36 |
| Year | 2000 | 2001 | 2002 |
| Temperature | 14.33 | 14.45 | 14.51 |
| Year | 2003 | 2004 | 2005 |
| Temperature | 14.52 | 14.48 | 14.55 |
| Year | 2006 | 2007 | 2008 |
| Temperature | 14.50 | 14.49 | 14.41 |
| Year | 2009 | 2010 | 2011 |
| Temperature | 14.50 | 14.56 | 14.43 |
| Year | 2012 | 2013 | 2014 |
| Temperature | 14.48 | 14.52 | 14.59 |
Question 14.19
14.19 Death by intent. Homicide and suicide are both intentional means of ending a life. However, the reason for committing a homicide is different than that for suicide, and we might expect homicide and suicide rates to be uncorrelated. On the other hand, both can involve some degree of violence, so perhaps we might expect some level of correlation in the rates. Table 14.1 gives data from 2008–2010 for 26 counties in Ohio. Rates are per 100,000 people. The data also indicate that the homicide rates for some counties should be treated with caution because of low counts (Y = Yes, treat with caution, and N = No, do not treat with caution).
(a) Make a scatterplot of the data for the counties for which the data do not need to be treated with caution. Use homicide rate as the explanatory variable.
(b) Is the association between these variables positive or negative? What is the form of the relationship? How strong is the relationship?
(c) Now add the data for the counties for which the data do need to be treated with caution to your graph, using a different color or a different plotting symbol. Does the pattern of the relationship that you observed in part (b) hold for the counties for which the data do need to be treated with caution also?
ta14-01
| County | Homicide rate |
Suicide rate |
Caution | County | Homicide rate |
Suicide rate |
Caution |
|---|---|---|---|---|---|---|---|
| Allen | 4.2 | 9.2 | Y | Lorrain | 3.1 | 11.0 | Y |
| Ashtabula | 1.8 | 15.5 | Y | Lucas | 7.4 | 13.3 | N |
| Butler | 2.6 | 12.7 | Y | Mahoning | 10.9 | 12.4 | N |
| Clermont | 1.0 | 16.0 | Y | Medina | 0.5 | 10.0 | Y |
| Clark | 5.6 | 14.5 | N | Miami | 2.6 | 9.2 | Y |
| Columbiana | 3.5 | 16.6 | N | Montgomery | 9.5 | 15.2 | N |
| Cuyahoga | 9.2 | 9.5 | N | Portage | 1.6 | 9.6 | Y |
| Delaware | 0.8 | 7.6 | Y | Stark | 4.7 | 13.5 | N |
| Franklin | 8.7 | 11.4 | N | Summit | 4.9 | 11.5 | N |
| Greene | 2.7 | 12.8 | Y | Trumbull | 5.8 | 16.6 | N |
| Hamilton | 8.9 | 10.8 | N | Warren | 0.7 | 11.3 | Y |
| Lake | 1.8 | 11.3 | Y | Wayne | 1.8 | 8.9 | Y |
| Licking | 4.5 | 12.9 | N | Wood | 1.0 | 7.4 | Y |
14.19 (b) Moderate, somewhat linear, and negative. (c) The pattern of the relationship in (b) does not hold for the counties that need the data to be treated with caution. The relationship appears much more weak and not negative for these counties.
Question 14.20
14.20 Marriage. Suppose that men always married women three years younger than themselves. Draw a scatterplot of the ages of six married couples, with the husband’s age as the explanatory variable. What is the correlation r for your data? Why?
Question 14.21
14.21 Stretching a scatterplot. Changing the units of measurement can greatly alter the appearance of a scatterplot. Return to the fossil data from Example 3:
| Femur: | 38 | 56 | 59 | 64 | 74 |
| Humerus: | 41 | 63 | 70 | 72 | 84 |
These measurements are in centimeters. Suppose a deranged scientist measured the femur in meters and the humerus in millimeters. The data would then be
| Femur: | 0.38 | 0.56 | 0.59 | 0.64 | 0.74 |
| Humerus: | 410 | 630 | 700 | 720 | 840 |
(a) Draw an x axis extending from 0 to 75 and a y axis extending from 0 to 850. Plot the original data on these axes. Then plot the new data on the same axes in a different color. The two plots look very different.
(b) Nonetheless, the correlation is exactly the same for the two sets of measurements. Why do you know that this is true without doing any calculations?
14.21 (b) Although changing the scales makes the scatterplot look very different, it has no impact on the correlation. Changing the units of the x and y variables does not change the correlation.
Question 14.22
14.22 Global warming. Exercise 14.18 gives data on the average global temperatures, in degrees Celsius, for the years 1994 to 2014.
(a) Use a calculator to find the correlation r. Explain from looking at the scatterplot why this value of r is reasonable.
(b) Suppose that the temperatures had been recorded in degrees Fahrenheit. For example, the 1994 temperature of 14.23°C would be 57.61°F. How would the value of r change?
Question 14.23
14.23 Death by intent. Table 14.1 gives data on on homicide and suicide rates from 2008–2010 for 26 counties in Ohio. The homicide rates for 14 of the counties should be treated with caution because of low counts. You made a scatterplot of these data in Exercise 14.19.
(a) Do you think the correlation will be about the same for the counties for which the data do need to be treated with caution and for the counties for which the data do not need to be treated with caution, or quite different for the two groups? Why?
(b) Calculate r for the counties for which the data do need to be treated with caution alone and also for for the counties for which the data do not need to be treated with caution alone. (Use your calculator.)
14.23 (a) It is unlikely the correlation will be about the same for the counties for which the data do not need to be treated with caution and for the counties for which the data do need to be treated with caution due to the low counts. (b) Counties with caution (low counts): r = .024; counties without caution: r = −.469.
Question 14.24
14.24 Strong association but no correlation. The gas mileage of an automobile first increases and then decreases as the speed increases. Suppose that this relationship is very regular, as shown by the following data on speed (miles per hour) and mileage (miles per gallon):
| Speed: | 25 | 35 | 45 | 55 | 65 |
| Mileage: | 20 | 24 | 26 | 24 | 20 |
Make a scatterplot of mileage versus speed. Use a calculator to show that the correlation between speed and mileage is r = 0. Explain why the correlation is 0 even though there is a strong relationship between speed and mileage.
Question 14.25
14.25 Death by intent. The data in Table 14.1 are given in deaths per 100,000 people. If we changed the data from deaths per 100,000 people to deaths per 1,000 people how would the rates change? How would the correlation between homicide and suicide rates change?
14.25 The rate would decrease (the decimal point in each value would move two places to the left). The correlation between homicide and suicide rates would stay the same.
Question 14.26
14.26 What are the units? How sensitive to changes in water temperature are coral reefs? To find out, measure the growth of corals in aquariums (where growth is the change in weight, in pounds, of the coral before and after the experiment) when the water temperature (in degrees Fahrenheit) is controlled at different levels. In what units are each of the following descriptive statistics measured?
(a) the mean growth of the coral
(b) the standard deviation of the growth of the coral
(c) the correlation between weight gain and temperature
(d) the median growth of the coral
Question 14.27
14.27 Teaching and research. A college newspaper interviews a psychologist about student ratings of the teaching of faculty members. The psychologist says, “The evidence indicates that the correlation between the research productivity and teaching rating of faculty members is close to zero.” The paper reports this as “Professor McDaniel said that good researchers tend to be poor teachers, and vice versa.” Explain why the paper’s report is wrong. Write a statement in plain language (don’t use the word “correlation”) to explain the psychologist’s meaning.
14.27 The newspaper interpreted zero correlation as implying a negative association between teaching ability and research productivity. The speaker meant that teacher rating and research productivity are not related (strictly speaking, that they are not linearly related).
Question 14.28
14.28 Sloppy writing about correlation. Each of the following statements contains a blunder. Explain in each case what is wrong.
(a) “There is a high correlation between the manufacturer of a car and the gas mileage of the car.”
(b) “We found a high correlation (r = 1.09) between the horsepower of a car and the gas mileage of the car.”
(c) “The correlation between the weight of a car and the gas mileage of the car was found to be r = 0.53 miles per gallon.”
Question 14.29
14.29 Guess the correlation. Measurements in large samples show that the correlation
(a) between this semester’s GPA and the previous semester’s GPA of an upper-class student is about ________.
(b) between IQ and the scores on a test of the reading ability of seventh-grade students is about ________.
(c) between the number of hours a student spends studying per week and the average number of hours spent studying by his or her roommates is about ________.
The answers (in scrambled order) are
r = 0.2 r = 0.5 r = 0.8
Match the answers to the statements and explain your choice.
14.29 (a) 0.8. (b) 0.5. (c) 0.2. Note that (a) will have the strongest relationship and (c) will have the weakest relationship.
Question 14.30
14.30 Guess the correlation. For each of the following pairs of variables, would you expect a substantial negative correlation, a substantial positive correlation, or a small correlation?
(a) the cost of a cable TV service and the number of channels provided by the service
(b) the weight of a road-racing bicycle and the cost of the bicycle
(c) the number of hours a student spends on Facebook and the student’s GPA
(d) the heights and salaries of faculty members at your university
ta14-02
| Team | Hot dog | Beer | Team | Hot dog | Beer | Team | Hot dog | Beer |
|---|---|---|---|---|---|---|---|---|
| Angels | 4.50 | 0.28 | Giants | 5.50 | 0.50 | Rays | 5.00 | 0.42 |
| Astros | 4.75 | 0.36 | Indians | 3.00 | 0.33 | Reds | 1.00 | 0.44 |
| Blue Jays | 4.98 | 0.49 | Marlins | 6.00 | 0.50 | Red Sox | 5.25 | 0.65 |
| Braves | 4.75 | 0.45 | Mets | 6.25 | 0.48 | Rockies | 4.75 | 0.38 |
| Brewers | 3.50 | 0.38 | Padres | 4.00 | 0.36 | Royals | 5.00 | 0.41 |
| Cardinals | 4.25 | 0.42 | Phillies | 3.75 | 0.37 | Tigers | 4.50 | 0.42 |
| Diamondbacks | 2.75 | 0.29 | Pirates | 3.25 | 0.34 | Twins | 4.50 | 0.38 |
| Dodgers | 5.50 | 0.31 | Rangers | 5.00 | 0.31 | White Sox | 4.00 | 0.41 |
Question 14.31
14.31 Investment diversification. A mutual funds company’s newsletter says, “A well-diversified portfolio includes assets with low correlations.” The newsletter includes a table of correlations between the returns on various classes of investments. For example, the correlation between municipal bonds and large-cap stocks is 0.50, and the correlation between municipal bonds and small-cap stocks is 0.21.
(a) Rachel invests heavily in municipal bonds. She wants to diversify by adding an investment whose returns do not closely follow the returns on her bonds. Should she choose large-cap stocks or small-cap stocks for this purpose? Explain your answer.
(b) If Rachel wants an investment that tends to increase when the return on her bonds drops, what kind of correlation should she look for?
14.31 (a) Small-cap stocks have a lower correlation with municipal bonds, so the relationship is weaker, which leads to greater diversification. (b) She should look for a negative correlation, although this would also mean that this investment tends to decrease when bond prices rise.
Question 14.32
14.32 Take me out to the ball game. What is the relationship between the price charged for a hot dog and the price charged, per ounce, for beer in Major League Baseball stadiums? Table 14.2 gives some data. Make a scatterplot appropriate for showing how beer price helps explain hot dog price. Describe the relationship that you see. Are there any outliers?
Question 14.33
14.33 When it rains, it pours. Figure 14.12 plots the highest yearly precipitation ever recorded in each state against the highest daily precipitation ever recorded in that state. The points for Alaska (AK), Hawaii (HI), and Texas (TX) are marked on the scatterplot.
(a) About what are the highest daily and yearly precipitation values for Alaska?
(b) Alaska and Hawaii have very high yearly maximums relative to their daily maximums. Omit these two states as outliers. Describe the nature of the relationship for the other states. Would knowing a state’s highest daily precipitation be a great help in predicting that state’s highest yearly precipitation?
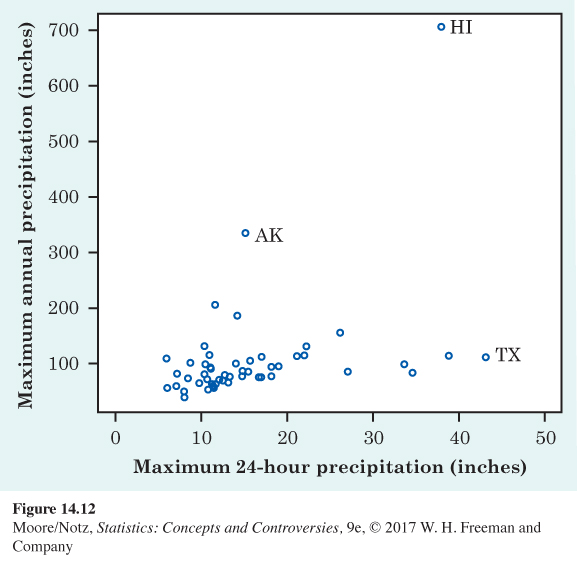
14.33 (a) The exact values for Alaska are 15.2 inches and 332.29 inches. (b) Without Alaska and Hawaii, the relationship is weakly positive and roughly linear. Knowing maximum 24-hour precipitation would be somewhat useful in predicting maximum annual precipitation for these other states, but the relationship is not very strong.
ex14-34
Question 14.34
14.34 How many corn plants is too many? How much corn per acre should a farmer plant to obtain the highest yield? To find the best planting rate, do an experiment: plant at different rates on several plots of ground and measure the harvest. Here are data from such an experiment:
(a) Is yield or planting rate the explanatory variable? Why?
(b) Make a scatterplot of yield and planting rate.
(c) Describe the overall pattern of the relationship. Is it a straight line? Is there a positive or negative association, or neither? Explain why increasing the number of plants per acre of ground has the effect that your graph shows.
| Plants per acre |
Yield (bushels per acre) |
|||
| 12,000 | 150.1 | 113.0 | 118.4 | 142.6 |
| 16,000 | 166.9 | 120.7 | 135.2 | 149.8 |
| 20,000 | 165.3 | 130.1 | 139.6 | 149.9 |
| 24,000 | 134.7 | 138.4 | 156.1 | |
| 28,000 | 119.0 | 150.5 | ||
ex14-35
Question 14.35
14.35 Why so small? Make a scatterplot of the following data:
| x | 1 | 2 | 3 | 4 | 9 | 10 |
| y | 12 | 2 | 3 | 5 | 9 | 11 |
Use your calculator to show that the correlation is about 0.4. What feature of the data is responsible for reducing the correlation to this value despite a strong straight-line association between x and y in most of the observations?
14.35 The correlation is r = 0.413. The correlation is greatly lowered by the one outlier. Outliers tend to have a fairly strong impact on correlation; it is much stronger here because there are so few observations.
Question 14.36
14.36 Ecological correlation. Many studies reveal a positive correlation between income and number of years of education. To investigate this, a researcher makes two plots.
Plot 1: Plot the number of years of education (the explanatory variable) versus the average annual income of all adults having that many years of education (the response variable).
Plot 2: Plot the number of years of education (the explanatory variable) versus the individual annual incomes of all adults (the response variable).
Which plot will display a stronger correlation? (Hint: Which plot will display a greater amount of scatter? In particular, will the variation from individual to individual having the same number of years of education create more or less scatter in Plot 2 compared with plotting the average incomes in Plot 1? What effect will increased scatter have on the strength of the association we observe?)
Note: A correlation based on averages rather than on individuals is called an ecological correlation. Correlations based on averages can be misleading if they are interpreted to be about individuals.
Question 14.37
14.37 Ecological correlation again. In Exercise 14.11 (page 330), would the association be stronger, weaker, or the same if the data given listed the GPAs of individual students (rather than averages) and the distance they lived from campus?

EXPLORING THE WEB
Follow the QR code to access exercises.