Probability rules
429
Because the probabilities in this example are just the proportions of all women who have each marital status, they follow rules that say how proportions behave. Here are some basic rules that any probability model must obey:
A. Any probability is a number between 0 and 1. Any proportion is a number between 0 and 1, so any probability is also a number between 0 and 1. An event with probability 0 never occurs, and an event with probability 1 occurs on every trial. An event with probability 0.5 occurs in half the trials in the long run.
B. All possible outcomes together must have probability 1. Because some outcome must occur on every trial, the sum of the probabilities for all possible outcomes must be exactly 1.
C. The probability that an event does not occur is 1 minus the probability that the event does occur. If an event occurs in (say) 70% of all trials, it fails to occur in the other 30%. The probability that an event occurs and the probability that it does not occur always add to 100%, or 1.
D. If two events have no outcomes in common, the probability that one or the other occurs is the sum of their individual probabilities. If one event occurs in 40% of all trials, a different event occurs in 25% of all trials, and the two can never occur together, then one or the other occurs on 65% of all trials because 40% + 25% = 65%.
EXAMPLE 1 Marital status of young women
Look again at the probabilities for the marital status of young women. Each of the four probabilities is a number between 0 and 1. Their sum is
0.478 + 0.476 + 0.004 + 0.042 = 1
This assignment of probabilities satisfies Rules A and B. Any assignment of probabilities to all individual outcomes that satisfies Rules A and B is legitimate. That is, it makes sense as a set of probabilities. Rules C and D are then automatically true. Here is an example of the use of Rule C.
The probability that the woman we draw is not married is, by Rule C,
P(not married) = 1 − P(married)
= 1 − 0.476 = 0.524
That is, if 47.6% are married, then the remaining 52.4% are not married. Rule D says that you can also find the probability that a woman is not married by adding the probabilities of the three distinct ways of being not married, as we did earlier. This gives the same result.
430
EXAMPLE 2 Rolling two dice
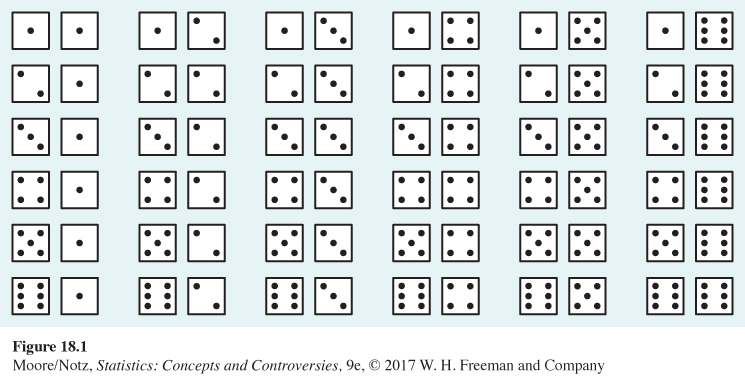
Rolling two dice is a common way to lose money in casinos. There are 36 possible outcomes when we roll two dice and record the up-faces in order (first die, second die). Figure 18.1 displays these outcomes. What probabilities should we assign?
Casino dice are carefully made. Their spots are not hollowed out, which would give the faces different weights, but are filled with white plastic of the same density as the red plastic of the body. For casino dice, it is reasonable to assign the same probability to each of the 36 outcomes in Figure 18.1. Because these 36 probabilities must have sum 1 (Rule B), each outcome must have probability 1/36, or 1-in-36.
We are interested in the sum of the spots on the up-faces of the dice. What is the probability that this sum is 5? The event “roll a 5” contains four outcomes, and its probability is the sum of the probabilities of these outcomes:
431
NOW IT’S YOUR TURN
Question 18.1
18.1 Rolling dice. Suppose you roll two casino dice, as in Example 2. What is the probability that the sum of the spots on the up-faces is 7? 11? 7 or 11?
The rules tell us only what probability models make sense. They don’t tell us whether the probabilities are correct, that is, whether they describe what actually happens in the long run. The probabilities in Example 2 are correct for casino dice. Inexpensive dice with hollowed-out spots are not balanced, and this probability model does not describe their behavior.
What about personal probabilities? Because they are personal, can’t they be anything you want them to be? If your personal probabilities don’t obey Rules A and B, you are entitled to your opinion, but we can say that your personal probabilities are incoherent. That is, they don’t go together in a way that makes sense. So we usually insist that personal probabilities for all the outcomes of a random phenomenon obey Rules A and B. That is, the same rules govern both kinds of probability. For example, if you believe that the Green Bay Packers, the New Orleans Saints, and the New England Patriots each have probability 0.4 of winning Super Bowl XLVII, your personal probabilities would not obey Rule B.