The reasoning of statistical tests of significance

The local hot-shot playground basketball player claims to make 80% of his free throws. “Show me,’’ you say. He shoots 20 free throws and makes eight of them. “Aha,’’ you conclude, “if he makes 80%, he would almost never make as few as eight of 20. So I don’t believe his claim.’’ That’s the reasoning of statistical tests of significance at the playground level: an outcome that is very unlikely if a claim is true is good evidence that the claim is not true.

Statistical inference uses data from a sample to draw conclusions about a population. So, once we leave the playground, statistical tests deal with claims about a population. Statistical tests ask if sample data give good evidence against a claim. A statistical test says, “If we took many samples and the claim were true, we would rarely get a result like this.’’ To get a numerical measure of how strong the sample evidence is, replace the vague term “rarely’’ by a probability. Here is an example of this reasoning at work.

EXAMPLE 1 Is the coffee fresh?

People of taste are supposed to prefer fresh-brewed coffee to the instant variety. But, perhaps, many coffee drinkers just need their caffeine fix. A skeptic claims that coffee drinkers can’t tell the difference. Let’s do an experiment to test this claim.

Each of 50 subjects tastes two unmarked cups of coffee and says which he or she prefers. One cup in each pair contains instant coffee; the other, fresh-brewed coffee. The statistic that records the result of our experiment is the proportion of the sample who say they like the fresh-brewed coffee better. We find that 36 of our 50 subjects choose the fresh coffee. That is,

To make a point, let’s compare our outcome with another possible result. If only 28 of the 50 subjects like the fresh coffee better than instant coffee, the sample proportion is

523

Surely 72% is stronger evidence against the skeptic’s claim than 56%. But how much stronger? Is even 72% in favor in a sample convincing evidence that a majority of the population prefer fresh coffee? Statistical tests answer these questions. Here’s the answer in outline form:

  • • The claim. The skeptic claims that coffee drinkers can’t tell fresh from instant so that only half will choose fresh-brewed coffee. That is, he claims that the population proportion p is only 0.5. Suppose for the sake of argument that this claim is true.

  • • The sampling distribution (from page 495). If the claim p = 0.5 were true and we tested many random samples of 50 coffee drinkers, the sample proportion would vary from sample to sample according to (approximately) the Normal distribution with

mean = p = 0.5

and

= 0.0707

Figure 22.1 displays this Normal curve.

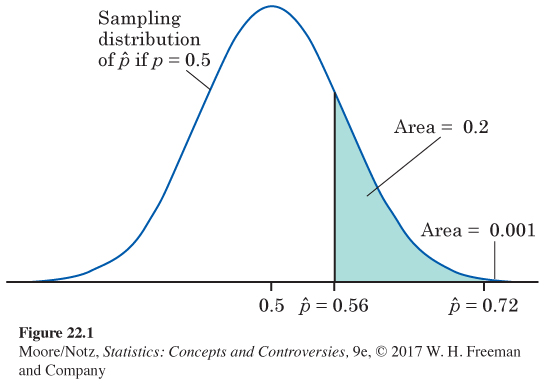
image
Figure 22.1: Figure 22.1 The sampling distribution of the proportion of 50 coffee drinkers who prefer fresh-brewed coffee if the truth about all coffee drinkers is that 50% prefer fresh coffee, Example 1. The shaded area is the probability that the sample proportion is 56% or greater.

524

  • • The data. Place the sample proportion on the sampling distribution. You see in Figure 22.1 that isn’t an unusual value but that is unusual. We would rarely get 72% of a sample of 50 coffee drinkers preferring fresh-brewed coffee if only 50% of all coffee drinkers felt that way. So, the sample data do give evidence against the claim.

  • • The probability. We can measure the strength of the evidence against the claim by a probability. What is the probability that a sample gives a this large or larger if the truth about the population is that p = 0.5? If , this probability is the shaded area under the Normal curve in Figure 22.1. This area is 0.20. Our sample actually gave . The probability of getting a sample outcome this large is only 0.001, an area too small to see in Figure 22.1. An outcome that would occur just by chance in 20% of all samples is not strong evidence against the claim. But an outcome that would happen only 1 in 1000 times is good evidence.

Be sure you understand why this evidence is convincing. There are two possible explanations of the fact that 72% of our subjects prefer fresh to instant coffee:

  1. 1. The skeptic is correct (p = 0.5), and by bad luck a very unlikely outcome occurred.

  2. 2. In fact, the population proportion favoring fresh coffee is greater than 0.5, so the sample outcome is about what would be expected.

We cannot be certain that Explanation 1 is untrue. Our taste test results could be due to chance alone. But the probability that such a result would occur by chance is so small (0.001) that we are quite confident that Explanation 2 is right.