PART II REVIEW EXERCISES
Review exercises are short and straightforward exercises that help you solidify the basic ideas and skills in each part of this book. We have provided “hints’’ that indicate where you can find the relevant material for the odd-numbered problems.
Question
II.1. Poverty in the states. Table II.1 gives the percentages of people living below the poverty line in the 26 states east of the Mississippi River. Make a stemplot of these data. Is the distribution roughly symmetric, skewed to the right, or skewed to the left? Which states (if any) are outliers? (Hint: See page 253.)
taII-01
| State | Percent | State | Percent | State | Percent |
|---|---|---|---|---|---|
| Alabama | 16.4 | Connecticut | 10.8 | Delaware | 13.7 |
| Florida | 15.1 | Georgia | 17.2 | Illinois | 12.9 |
| Indiana | 13.4 | Kentucky | 18.9 | Maine | 12.5 |
| Maryland | 10.1 | Massachusetts | 11.6 | Michigan | 14.1 |
| Mississippi | 22.2 | New Hampshire | 8.6 | New Jersey | 10.2 |
| New York | 15.9 | North Carolina | 17.9 | Ohio | 14.5 |
| Pennsylvania | 13.1 | Rhode Island | 13.6 | South Carolina | 16.3 |
| Tennessee | 18.4 | Vermont | 10.0 | Virginia | 10.5 |
| West Virginia | 17.0 | Wisconsin | 11.2 | ||
| Source: www.census.gov/hhes/www/poverty/data/index.html | |||||
II.1 The distribution could be considered slightly right skewed or roughly symmetric with New Hampshire and Mississippi as outliers.
Question
II.2. Quarterbacks. Table II.2 gives the total passing yards for National Football League starting quarterbacks during the 2014 season. (These are the quarterbacks with the most passing yards on each team.) Make a histogram of these data. Does the distribution have a clear shape: roughly symmetric, clearly skewed to the left, clearly skewed to the right, or none of these? Which quarterbacks (if any) are outliers?
taII-02
| Quarterback | Yards | Quarterback | Yards |
|---|---|---|---|
| Blake Bortels | 2908 | Josh McCown | 2206 |
| Tom Brady | 4109 | Zach Mettenberger | 1412 |
| Drew Brees | 4952 | Cam Newton | 3127 |
| Teddy Bridgewater | 2919 | Kyle Orton | 3018 |
| Derek Carr | 3270 | Philip Rivers | 4286 |
| Kirk Cousins | 1710 | Aaron Rodgers | 4381 |
| Jay Cutler | 3812 | Ben Roethlisberger | 4952 |
| Andy Dalton | 3398 | Tony Romo | 3705 |
| Austin Davis | 2001 | Matt Ryan | 4694 |
| Ryan Fitzpatrick | 2483 | Mark Sanchez | 2418 |
| Joe Flacco | 3986 | Alex Smith | 3265 |
| Brian Hoyer | 3326 | Geno Smith | 2525 |
| Colin Kaepernick | 3369 | Matthew Stafford | 4257 |
| Andrew Luck | 4761 | Drew Stanton | 1711 |
| Eli Manning | 4410 | Ryan Tannehill | 4045 |
| Peyton Manning | 4727 | Russell Wilson | 3475 |
| Source: www.pro-football-reference.com/years/2014/passing.htm. | |||
Question
II.3. Poverty in the states. Give the five-number summary for the data on poverty from Table II.1. (Hint: See page 272.)
II.3 min = 8.6, Q1=11.2, Med = 13.65, Q3 = 16.4, max = 22.2.
Question
II.4. Quarterbacks. Give the five-number summary for the data on passing yards for NFL quarterbacks from Table II.2.
Question
II.5. Poverty in the states. Find the mean percentage of state residents living in poverty from the data in Table II.1. If we removed Mississippi from the data, would the mean increase or decrease? Why? Find the mean for the 25 remaining states to verify your answer. (Hint: See page 277.)
II.5 The mean for all states in Table II.1 is 14.081. Mississippi is a high outlier, so we would expect the mean to decrease. The mean without Mississippi is 13.756.
Question
II.6. Big heads? The army reports that the distribution of head circumference among male soldiers is approximately Normal with mean 22.8 inches and standard deviation 1.1 inches. Use the 68–95–99.7 rule to answer these questions.
(a) Between what values do the middle 95% of head circumferences fall?
(b) What percentage of soldiers have head circumferences greater than 23.9 inches?
Question
II.7. SAT scores. The scale for SAT exam scores is set so that the distribution of scores is approximately Normal with mean 500 and standard deviation 100. Answer these questions without using a table.
(a) What is the median SAT score? (Hint: See page 299.)
(b) You run a tutoring service for students who score between 400 and 600 and hope to attract many students. What percentage of SAT scores are between 400 and 600? (Hint: See page 300.)
II.7 (a) 500. (b) 68%.
Question
II.8. Explaining correlation. You have data on the yearly wine consumption (liters of alcohol from drinking wine per person) and yearly deaths from cirrhosis of the liver for several developed countries. Say as specifically as you can what the correlation r between yearly wine consumption and yearly deaths from cirrhosis of the liver measures.
Question
II.9. Data on snakes. For a biology project, you measure the length (inches) and weight (ounces) of 12 snakes of the same variety. What units of measurement do each of the following have?
(a) The mean length of the snakes. (Hint: See page 277.)
(b) The first quartile of the snake lengths. (Hint: See page 270.)
(c) The standard deviation of the snake lengths. (Hint: See page 277.)
(d) The correlation between length and snake weight. (Hint: See page 325.)
II.9 (a) Inches. (b) Inches. (c) Inches. (d) No units.
Question
II.10. More data on snakes. For a biology project, you measure the length (inches) and weight (ounces) of 12 snakes of the same variety.
(a) Explain why you expect the correlation between length and weight to be positive.
(b) The mean length turns out to be 20.8 inches. What is the mean length in centimeters? (There are 2.54 centimeters in an inch.)
(c) The correlation between length and weight turns out to be r = 0.6. If you were to measure length in centimeters instead of inches, what would be the new value of r?
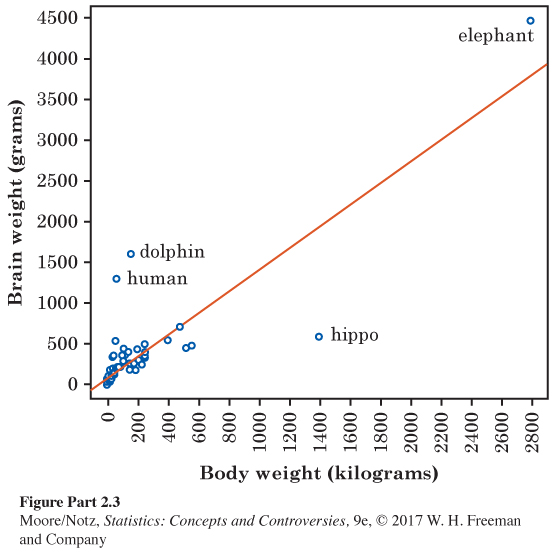
Figure II.3 plots the average brain weight in grams versus average body weight in kilograms for many species of mammals. There are many small mammals whose points at the lower left overlap. Exercises II.11 through II.16 are based on this scatterplot.
Question
II.11. Dolphins and hippos. The points for the dolphin and hippopotamus are labeled in Figure II.3. Read from the graph the approximate body weight and brain weight for these two species. (Hint: See page 318.)
II.11 Dolphin: 180 kg, 1600 g. Hippo: 1400 kg, 600 g.
Question
II.12. Dolphins and hippos. One reaction to this scatterplot is “Dolphins are smart; hippos are dumb.’’ What feature of the plot lies behind this reaction?
Question
II.13. Outliers. African elephants are much larger than any other mammal in the data set but lie roughly in the overall straight-line pattern. Dolphins, humans, and hippos lie outside the overall pattern. The correlation between body weight and brain weight for the entire data set is r = 0.86.
(a) If we removed elephants, would this correlation increase, decrease, or not change much? Explain your answer. (Hint: See page 326.)
(b) If we removed dolphins, hippos, and humans, would this correlation increase, decrease, or not change much? Explain your answer. (Hint: See page 326.)
II.13 (a) Decrease because that plot looks more linear with elephants. That is, if we drew a line through that scatterplot, there is a less relative scatter about that line with elephants than without. (b) Increase, because that plot looks less linear with dolphins, hippos, and humans. That is, is we drew a line through the scatterplot, there is more relative scatter about that line with dolphins, hippos, and humans than without.
Question
II.14. Brain and body. The correlation between body weight and brain weight is r = 0.86. How well does body weight explain brain weight for mammals? Compute r2 to answer this question, and briefly explain what r2 tells us.
Question
II.15. Prediction. The line on the scatterplot in Figure II.3 is the least-squares regression line for predicting brain weight from body weight. Suppose that a new mammal species with body weight 600 kilograms is discovered hidden in the rain forest. Predict the brain weight for this species. (Hint: See page 340.)
II.15 800 g.
Question
II.16. Slope. The line on the scatter-plot in Figure II.3 is the least-squares regression line for predicting brain weight from body weight. The slope of this line is one of the numbers below. Which number is the slope? Why?
(a) b = 0.5.
(b) b = 1.3.
(c) b = 3.2.
From Rex Boggs in Australia comes an unusual data set: before showering in the morning, he weighed the bar of soap in his shower stall. The weight goes down as the soap is used. The data appear in Table II.3 (weights in grams). Notice that Mr. Boggs forgot to weigh the soap on some days. Exercises II.17, II.18, and II.19 are based on the soap data set.
taII-03
| Day | Weight | Day | Weight | Day | Weight |
|---|---|---|---|---|---|
| 1 | 124 | 8 | 84 | 16 | 27 |
| 2 | 121 | 9 | 78 | 18 | 16 |
| 5 | 103 | 10 | 71 | 19 | 12 |
| 6 | 96 | 12 | 58 | 20 | 8 |
| 7 | 90 | 13 | 50 | 21 | 6 |
| Source: Rex Boggs. | |||||
Question
II.17. Scatterplot. Plot the weight of the bar of soap against day. Is the overall pattern roughly straight-line? Based on your scatterplot, is the correlation between day and weight close to 1, positive but not close to 1, close to 0, negative but not close to −1, or close to −1? Explain your answer. (Hint: See page 325.)
II.17 Roughly a straight line with r close to −1. From use, soap shrinks in size.
Question
II.18. Regression. The equation for the least-squares regression line for the data in Table II.3 is
weight = 133.2 − 6.31 × day
(a) Explain carefully what the slope b = −6.31 tells us about how fast the soap lost weight.
(b) Mr. Boggs did not measure the weight of the soap on Day 4. Use the regression equation to predict that weight.
(c) Draw the regression line on your scatterplot from the previous exercise.
Question
II.19. Prediction? Use the regression equation in the previous exercise to predict the weight of the soap after 30 days. Why is it clear that your answer makes no sense? What’s wrong with using the regression line to predict weight after 30 days? (Hint: See page 345.)
II.19 −56.1 g., the soap could not weigh a negative amount; prediction outside the range of the available data is risky.
Question
II.20. Keeping up with the Joneses. The Jones family had a household income of $30,000 in 1980, when the average CPI (1982–84 = 100) was 82.4. The average CPI for 2014 was 236.7. How much must the Joneses earn in 2014 to have the same buying power they had in 1980?
Question
II.21. Affording a Mercedes. A Mercedes-Benz 190 cost $24,000 in 1981, when the average CPI (1982–84 = 100) was 90.9. The average CPI for 2014 was 236.7. How many 2014 dollars must you earn to have the same buying power as $24,000 had in 1981? (Hint: See page 372.)
II.21$24000×236.790.9=$62,495.05.
Question
II.22. Affording a Steinway. A Steinway concert grand piano cost $13,500 in 1976. A similar Steinway cost $163,600 in August 2015. Has the cost of the piano gone up or down in real terms? Using Table 16.1 and the fact that the August 2015 CPI was 238.7, give a calculation to justify your answer.
exII-23
Question
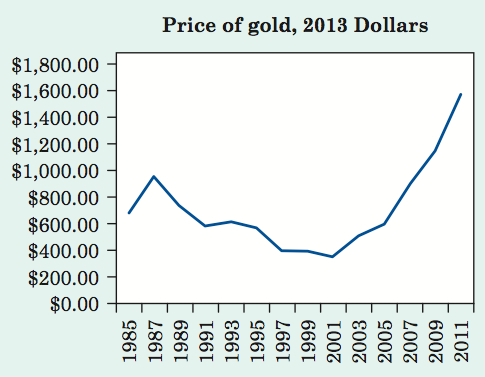
II.23. The price of gold. Some people recommend that investors buy gold “to protect against inflation.’’ Here are the prices of an ounce of gold at the end of the year for the years between 1985 and 2013. Using Table 16.1, make a graph that shows how the price of gold changed in real terms over this period. Would an investment in gold have protected against inflation by holding its value in real terms?
| Year: | 1985 | 1987 | 1989 | 1991 | 1993 |
| Gold price: | $327 | $484 | $399 | $353 | $392 |
| Year: | 1995 | 1997 | 1999 | 2001 | 2003 |
| Gold price: | $387 | $290 | $290 | $277 | $416 |
| Year: | 2005 | 2007 | 2009 | 2011 | 2013 |
| Gold price: | $513 | $834 | $1088 | $1531 | $1204 |
(Hint: See page 372.)
II.23 While the value of gold dropped from 1987 to 2001 (in terms of 2013 dollars), an investment in gold most certainly holds its value today.
Question
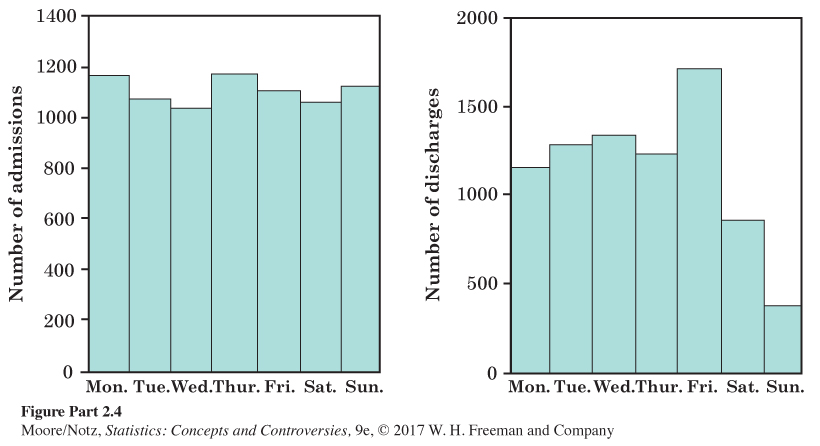
II.24. Never on Sunday? The Canadian province of Ontario carries out statistical studies to monitor how Canada’s national health care system is working in the province. The bar graphs in Figure II.4 come from a study of admissions and discharges from community hospitals in Ontario. They show the number of heart attack patients admitted and discharged on each day of the week during a two-year period.
(a) Explain why you expect the number of patients admitted with heart attacks to be roughly the same for all days of the week. Do the data show that this is true?
(b) Describe how the distribution of the day on which patients are discharged from the hospital differs from that of the day on which they are admitted. What do you think explains the difference?
exII-25
Question
II.25. Drive time. Professor Moore, who lives a few miles outside a college town, records the time he takes to drive to the college each morning. Here are the times (in minutes) for 42 consecutive weekdays, with the dates in order along the rows:
| 8.25 | 7.83 | 8.30 | 8.42 | 8.50 | 8.67 | 8.17 |
| 9.00 | 9.00 | 8.17 | 7.92 | 9.00 | 8.50 | 9.00 |
| 7.75 | 7.92 | 8.00 | 8.08 | 8.42 | 8.75 | 8.08 |
| 9.75 | 8.33 | 7.83 | 7.92 | 8.58 | 7.83 | 8.42 |
| 7.75 | 7.42 | 6.75 | 7.42 | 8.50 | 8.67 | 10.17 |
| 8.75 | 8.58 | 8.67 | 9.17 | 9.08 | 8.83 | 8.67 |
(b) Make a line graph of the drive times. (Label the horizontal axis in days, 1 to 42.) The plot shows no clear trend, but it does show one unusually low drive time and two unusually high drive times. Circle these observations on your plot. (Hint: See page 223.)
II.25 (a) Roughly symmetric; the two highest and one lowest time might be considered outliers.
Question
II.26. Drive time outliers. In the previous exercise, there are three outliers in Professor Moore’s drive times to work. All three can be explained. The low time is the day after Thanksgiving (no traffic on campus). The two high times reflect delays due to an accident and icy roads. Remove these three observations. To summarize normal drive times, use a calculator to find the mean ˉx and standard deviation s of the remaining 39 times.
Question
 II.27. House prices. An April 15, 2014, article in the Los Angeles Times reported that the median housing price in Southern California was about $400,000. Would the mean housing price be higher, about the same, or lower? Why? (Hint: See page 281.)
II.27. House prices. An April 15, 2014, article in the Los Angeles Times reported that the median housing price in Southern California was about $400,000. Would the mean housing price be higher, about the same, or lower? Why? (Hint: See page 281.)
II.27 The mean would be higher because housing prices tend to have a right-skewed distribution. Unusually expensive houses would cause the mean to increase and be larger than the median.
taII-04
| State | Percent | State | Percent | State | Percent |
|---|---|---|---|---|---|
| Alabama | 38.4 | Louisiana | 40.6 | Ohio | 50.7 |
| Alaska | 40.8 | Maine | 56.3 | Oklahoma | 33.2 |
| Arizona | 44.6 | Maryland | 62.0 | Oregon | 54.2 |
| Arkansas | 36.9 | Massachusetts | 60.7 | Pennsylvania | 52.0 |
| California | 60.2 | Michigan | 54.2 | Rhode Island | 62.7 |
| Colorado | 51.5 | Minnesota | 52.3 | South Carolina | 44.1 |
| Connecticut | 58.1 | Mississippi | 43.8 | South Dakota | 39.9 |
| Delaware | 58.6 | Missouri | 44.4 | Tennessee | 39.1 |
| Florida | 50.0 | Montana | 41.7 | Texas | 41.4 |
| Georgia | 45.5 | Nebraska | 38.0 | Utah | 24.8 |
| Hawaii | 70.6 | Nevada | 52.4 | Vermont | 66.6 |
| Idaho | 32.6 | New Hampshire | 52.0 | Virginia | 51.2 |
| Illinois | 57.6 | New Jersey | 58.4 | Washington | 56.2 |
| Indiana | 43.9 | New Mexico | 53.0 | West Virginia | 35.5 |
| Iowa | 52.0 | New York | 63.4 | Wisconsin | 52.8 |
| Kansas | 38.0 | North Carolina | 48.4 | Wyoming | 27.8 |
| Kentucky | 37.8 | North Dakota | 38.7 | ||
| Source: uselectionatlas.org/. | |||||
Question
II.28. The 2012 election. Barack Obama was elected president in 2012 with 51.1% of the popular vote. His Republican opponent, Mitt Romney, received 47.2% of the vote, with minor candidates taking the remaining votes. Table II.4 gives the percentage of the popular vote won by President Obama in each state. Describe these data with a graph, a numerical summary, and a brief verbal description.
Question
II.29. Statistics for investing. Joe’s retirement plan invests in stocks through an “index fund’’ that follows the behavior of the stock market as a whole, as measured by the Standard & Poor’s 500 index. Joe wants to buy a mutual fund that does not track the index closely. He reads that monthly returns from Fidelity Technology Fund have correlation r = 0.77 with the S&P 500 index and that Fidelity Real Estate Fund has correlation r = 0.37 with the index.
(a) Which of these funds has the closer relationship to returns from the stock market as a whole? How do you know? (Hint: See page 325.)
(b) Does the information given tell Joe anything about which fund has had higher returns? (Hint: See page 328.)
II.29 (a) Fidelity Technology Fund because of the higher correlation. (b) No.