9.6 Problem Solving: Working It Out
You have a problem when you find yourself in a place where you don’t want to be. In such circumstances, you try to find a way to change the situation so that you end up in a situation you do want. Let’s say that it’s the night before a test, and you are trying to study but just can’t settle down and focus on the material. This is a situation you don’t want. So, you try to think of ways to help yourself focus. You might begin with the material that most interests you, or provide yourself with rewards, such as a music break or trip to the refrigerator. If these activities enable you to get down to work, your problem is solved.
Two major types of problems complicate our daily lives. The first and most frequent is the ill-
Means–Ends Analysis

In 1945, German psychologist Karl Duncker reported some important studies of the problem-
- Analyze the goal state (i.e., the desired outcome you want to attain).
- Analyze the current state (i.e., your starting point, or the current situation).
- List the differences between the current state and the goal state.
- Reduce the list of differences by
- Direct means (a procedure that solves the problem without intermediate steps).
- Generating a subgoal (an intermediate step on the way to solving the problem).
- Finding a similar problem that has a known solution.
Consider, for example, one of Duncker’s problems:
A patient has an inoperable tumor in his abdomen. The tumor is inoperable because it is surrounded by healthy but fragile tissue that would be severely damaged during surgery. How can the patient be saved?
The goal state is a patient without the tumor and with undamaged surrounding tissue. The current state is a patient with an inoperable tumor surrounded by fragile tissue. The difference between these two states is the tumor. A direct-
Analogical Problem Solving
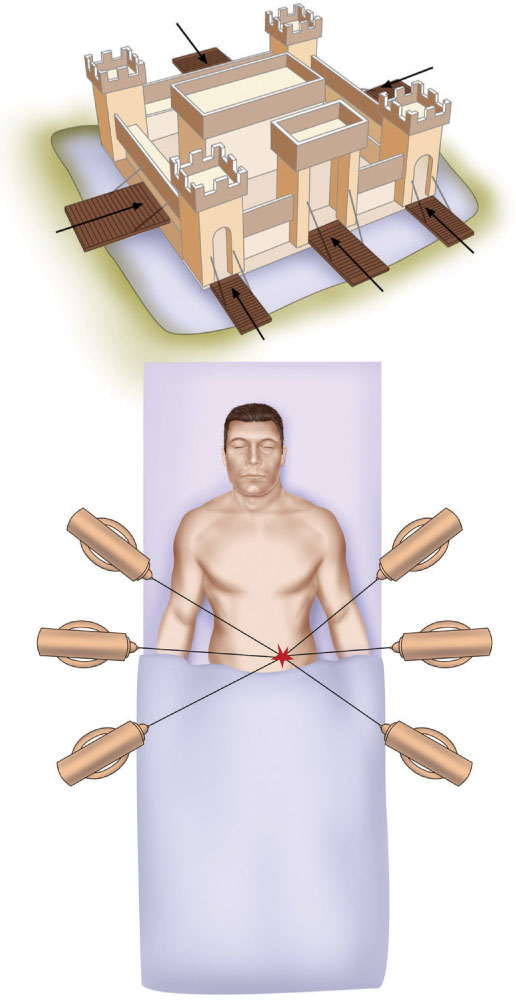
 Figure 9.13: Analogical Problem Solving Just as smaller, lighter battalions can reach the fortress without damaging the bridges, many small X-
Figure 9.13: Analogical Problem Solving Just as smaller, lighter battalions can reach the fortress without damaging the bridges, many small X-When we engage in analogical problem solving, we attempt to solve a problem by finding a similar problem with a known solution and applying that solution to the current problem. Consider the following story:
An island surrounded by bridges is the site of an enemy fortress. The massive fortification is so strongly defended that only a very large army could overtake it. Unfortunately, the bridges would collapse under the weight of such a huge force. So, a clever general divides the army into several smaller units and sends the units over different bridges, timing the crossings so that the many streams of soldiers converge on the fortress at the same time and the fortress is taken.
Does this story suggest a solution to the tumor problem? It should. Removing a tumor and attacking a fortress are very different problems, but the two problems are analogous because they share a common structure: The goal state is a conquered fortress with undamaged surrounding bridges. The current state is an occupied fortress surrounded by fragile bridges. The difference between the two states is the occupying enemy. The solution is to divide the required force into smaller units that are light enough to spare the fragile bridges and send them down the bridges simultaneously so that they converge on the fortress. The combined units will form an army strong enough to take the fortress (see FIGURE 9.13).
This analogous problem of the island fortress suggests the following direct-
Surround the patient with X-
Did this solution occur to you after reading the fortress story? In studies that have used the tumor problem, only 10% of participants spontaneously generated the correct solution. This percentage rose to 30% if participants read the island fortress problem or other analogous story. However, the success climbed dramatically to 75% among participants who had a chance to read more than one analogous problem or were given a deliberate hint to use the solution to the fortress story (Gick & Holyoak, 1980).
384
Why are analogies useful in problem solving?
Why was the fortress problem so ineffective by itself? Problem solving is strongly affected by superficial similarities between problems, and the relationship between the tumor and fortress problems lies deep in their structure (Catrambone, 2002).
Creativity and Insight
Analogical problem solving shows us that successfully solving a problem often depends on learning the principles underlying a particular type of problem and also that solving lots of problems improves our ability to recognize certain problem types and generate effective solutions. Some problem solving, however, seems to involve brilliant flashes of insight and creative solutions that have never before been tried. Creative and insightful solutions often rely on restructuring a problem so that it turns into a problem you already know how to solve (Cummins, 2012).
Genius and Insight
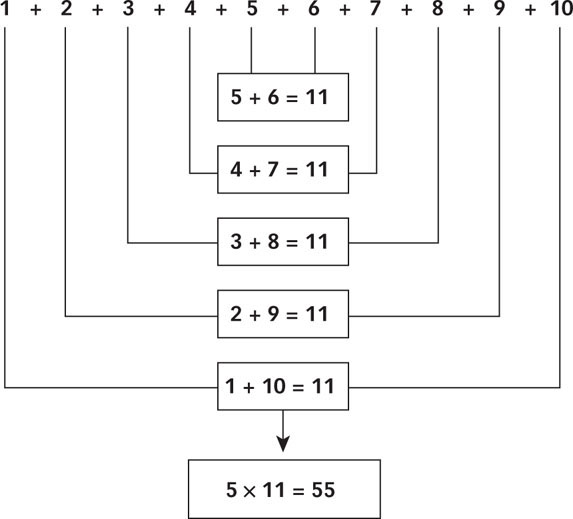
 Figure 9.14: Genius and Insight Young Friedrich Gauss imagined the scheme shown here and quickly reduced a laborious addition problem to an easy multiplication task. Gauss’s early insight led him to realize later an intriguing truth: This simple solution generalizes to number series of any length.
Figure 9.14: Genius and Insight Young Friedrich Gauss imagined the scheme shown here and quickly reduced a laborious addition problem to an easy multiplication task. Gauss’s early insight led him to realize later an intriguing truth: This simple solution generalizes to number series of any length.
Consider the exceptional mind of the mathematician Friedrich Gauss (1777–1855). One day, Gauss’s elementary schoolteacher asked the class to add up the numbers 1 through 10. While his classmates laboriously worked their sums, Gauss had a flash of insight that caused the answer to occur to him immediately. Gauss imagined the numbers 1 through 10 as weights lined up on a balance beam, as shown in FIGURE 9.14. Starting at the left, each “weight” increases by 1. In order for the beam to balance, each weight on the left must be paired with a weight on the right. You can see this by starting at the middle and noticing that 5 + 6 = 11, then moving outward, 4 + 7 = 11, 3 + 8 = 11, and so on. This produces five number pairs that add up to 11. Now the problem is easy. Multiply. Gauss’s genius lay in restructuring the problem in a way that allowed him to notice a very simple and elegant solution to an otherwise tedious task–a procedure, by the way, that generalizes to series of any length.
What is the role of the unconscious in flashes of insight?
According to Gestalt psychologists, insights such as these reflect a spontaneous restructuring of a problem. A sudden flash of insight contrasts with incremental problem-
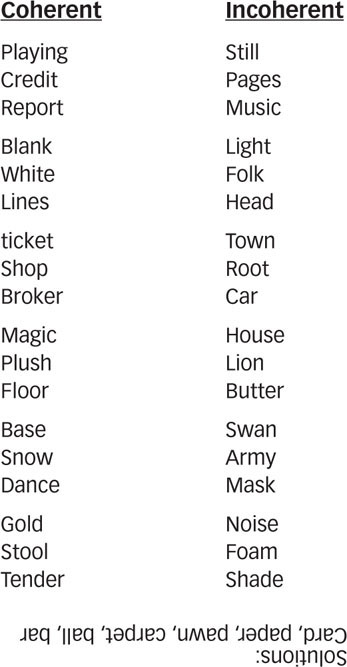
 Figure 9.15: Insightful Solutions Are Really Incremental Participants were asked to find a fourth word that was associated with the other three words in each series. Even if I they couldn’t find a solution, they could reliably choose which series of three words were solvable and which were not. Try to solve these.
Figure 9.15: Insightful Solutions Are Really Incremental Participants were asked to find a fourth word that was associated with the other three words in each series. Even if I they couldn’t find a solution, they could reliably choose which series of three words were solvable and which were not. Try to solve these.
Later research, however, suggests that sudden insightful solutions may actually result from unconscious incremental processes (Bowers et al., 1990). In one study, research participants were shown paired, three-
Even if participants couldn’t find a solution, they could reliably decide, more than by chance alone, which of the pairs was coherent. However, if insightful solutions actually occur in a sudden, all-
385
Finding a connection between the words strawberry and traffic might take some time, even for someone motivated to figure out how they are related. But if the word strawberry activates jam in long-
Functional Fixedness

 Figure 9.16: Functional Fixedness and the Candle Problem How can you use these objects–a box of matches, thumbtacks, and a candle–to mount the candle on the wall so that it illuminates the room? Give this problem some thought before you check the answer in Figure 9.19.
Figure 9.16: Functional Fixedness and the Candle Problem How can you use these objects–a box of matches, thumbtacks, and a candle–to mount the candle on the wall so that it illuminates the room? Give this problem some thought before you check the answer in Figure 9.19.
If insight is a simple incremental process, why isn’t its occurrence more frequent? In the research discussed previously, participants produced insightful solutions only 25% of the time. Insight is rare because problem solving (like decision making) suffers from framing effects. In problem solving, framing tends to limit the types of solutions that occur to us. Functional fixedness–the tendency to perceive the functions of objects as fixed–is a process that constricts our thinking. Look at FIGURES 9.16 and 9.17 and see if you can solve the problems before reading on. In Figure 9.16, your task is to illuminate a dark room using the following objects: some thumbtacks, a box of matches, and a candle. In Figure 9.17, your task is to use the items on the table to find a way to hold on to a string hanging from the ceiling and at the same time reach a second string that is too far away to grasp.

 Figure 9.17: Functional Fixedness and the String Problem The strings hung from hooks on either side of the ceiling are long enough to be tied together, but they are positioned too far apart to reach one while holding on to the other. Using the tools shown on the table (nails, matches and a hammer), how can you accomplish the task? Compare your answer to that in Figure 9.20.
Figure 9.17: Functional Fixedness and the String Problem The strings hung from hooks on either side of the ceiling are long enough to be tied together, but they are positioned too far apart to reach one while holding on to the other. Using the tools shown on the table (nails, matches and a hammer), how can you accomplish the task? Compare your answer to that in Figure 9.20.
386

 Figure 9.18: The Nine-
Figure 9.18: The Nine-Difficulty solving these problems derives from our tendency to think of the objects only in terms of their normal, typical, or “fixed” functions. We don’t think to use the matchbox for a candleholder because boxes typically hold matches, not candles. Similarly, using the hammer as a pendulum weight doesn’t spring to mind because hammers are typically used to pound things. Did functional fixedness prevent you from solving these problems? (The solutions are shown in FIGURES 9.19 and 9.20.)
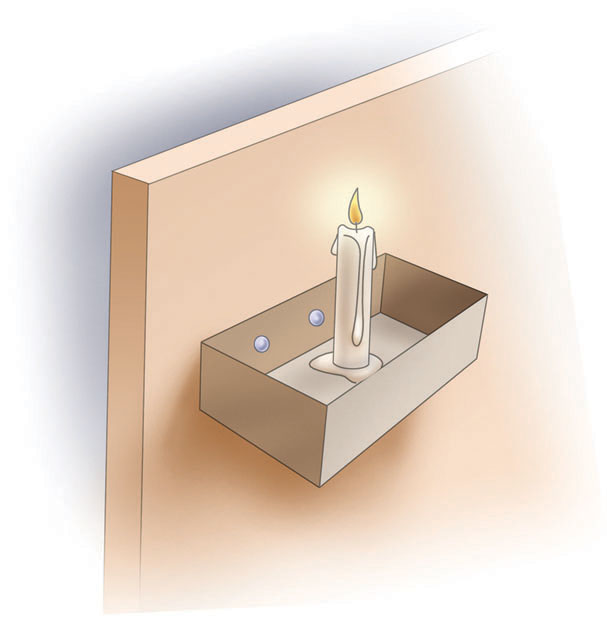
 Figure 9.19: The Solution to the Candle Problem What makes this problem difficult is that the usual function of the box (to hold matches) interferes with recognizing that it can be tacked to the wall to serve as a candleholder.
Figure 9.19: The Solution to the Candle Problem What makes this problem difficult is that the usual function of the box (to hold matches) interferes with recognizing that it can be tacked to the wall to serve as a candleholder.

 Figure 9.20: The Solution to the String Problem The usual function of the hammer (to pound things) interferes with recognizing that it can also serve as a weighted pendulum to swing the string into the person’s grasp.
Figure 9.20: The Solution to the String Problem The usual function of the hammer (to pound things) interferes with recognizing that it can also serve as a weighted pendulum to swing the string into the person’s grasp.
Sometimes framing limits our ability to generate a solution. Before reading on, look at FIGURE 9.18. Without lifting your pencil from the page, try to connect all nine dots with only four straight lines. To solve this problem, you must allow the lines you draw to extend outside the imaginary box that surrounds the dots (see FIGURE 9.21). This constraint does not reside in the problem but in the mind of the problem solver (Kershaw & Ohlsson, 2004). Despite the apparent sudden flash of insight that seems to yield a solution to problems of this type, research indicates that the thought processes people use when solving even this type of insight problem are best described as an incremental, means–ends analysis (MacGregor, Ormerod, & Chronicle, 2001).
HOT SCIENCE: Sudden Insight and the Brain
The “aha!” moment that accompanies a sudden flash of insight is a compelling experience, one that highlights that solving a problem based on insight feels radically different from solving it through step-

 Figure 9.21: Two Solutions to the Nine-
Figure 9.21: Two Solutions to the Nine-To examine brain activity associated with insight, researchers used a procedure called compound remote associates that is similar in some respects to the three-
Participants are instructed to press a button the moment a solution comes to mind, then describe whether they arrived at the solution via insight or through an analytic strategy. In an initial study, researchers used the electroencephalograph (EEG; see the Neuroscience chapter) to measure brain electrical activity as participants attempted to solve the problems. What they observed was striking: Beginning about one-
The great French scientist Louis Pasteur once stated: “Chance favors only the prepared mind.” Inspired by this observation, researchers asked whether brain activity occurring just before presentation of a problem influenced whether that problem was solved via insight or analytic strategies (Kounios et al., 2006). It did. In the moments before a problem was solved with an insight solution, there was increased activity deep in the frontal lobes, in a part of the brain known as the anterior cingulate, which controls cognitive processes such as the ability to switch attention from one thing to another. The researchers suggested that this increased activity in the anterior cingulate allowed participants to attend to and detect associations that were only weakly activated, perhaps at a subconscious level, and that facilitate sudden insight.
A related study with the compound remote associates task revealed that when people were in a positive mood, they solved more problems with insight than people who were in a less positive mood (Subramaniam et al., 2009). Moreover, as shown in the figure, positive mood was associated with heightened activity in the anterior cingulate during the moments before a problem was presented–suggesting that being in a positive mood helps to prepare the brain for sudden insight by “turning on” the anterior cingulate and thereby increasing one’s ability to detect associations that aid problem solution. This link between positive mood and insight might help explain a striking recent finding: Moderate levels of alcohol intoxication resulted in enhanced performance on the remote associates task, and also produced a stronger feeling that problem solutions are the result of sudden insight (Jarosz, Colflesh, & Wiley, 2012). Alternatively, the beneficial effects of alcohol could be attributable to a reduction in controlled, focused processing, which frees up the ability to generate distant associations.
387
Brain activity prior to problem solving provides clues about which individuals are more likely to rely on insight over analytic strategies to solve compound remote associates (Kounios et al., 2008). Using EEG to measure resting brain activity, researchers found that insight problem solvers showed more resting activity in the right cerebral hemisphere than did analytic problem solvers, which is consistent with other research linking creativity with right-
The results of these studies suggest that the familiar image of a light bulb going off in your head when you experience an “aha!” moment is on the mark: Those moments are indeed accompanied by something like an electrical power surge in the brain, and are preceded by specific types of electrical activity patterns. It seems likely that future research will tell us much more about how to turn on the mental light bulb and keep it burning bright.

 Like concept formation and decision making, problem solving is a process in which new inputs (in this case, problems) are interpreted in terms of old knowledge. Problems may be ill defined or well defined, leading to more or less obvious solutions.
Like concept formation and decision making, problem solving is a process in which new inputs (in this case, problems) are interpreted in terms of old knowledge. Problems may be ill defined or well defined, leading to more or less obvious solutions. The solutions we generate depend as much on the organization of our knowledge as they do on the objective characteristics of the problems. Means–ends analysis and analogical problem solving offer pathways to effective solutions, although we often frame things in terms of what we already know and already understand.
The solutions we generate depend as much on the organization of our knowledge as they do on the objective characteristics of the problems. Means–ends analysis and analogical problem solving offer pathways to effective solutions, although we often frame things in terms of what we already know and already understand. Sometimes, as in the case of functional fixedness, that knowledge can restrict our problem-
Sometimes, as in the case of functional fixedness, that knowledge can restrict our problem-solving processes, making it difficult to find solutions that should be easy to find.
388