4.3 How Does GPS Find Your Position?

At this point, the three segments of GPS have satellites broadcasting signals, ground stations monitoring and correcting those signals, and users receiving those signals—and all three of these segments work together to determine your position on Earth’s surface. The signals being sent from the satellites are the key to the whole process—the signals contain information about the satellite’s status, the orbit, and the location (referred to as the almanac) that’s sending them, as well as more precise data about satellite location (this information is referred to as the ephemeris).

The information is sent in one of two digital pseudo-random codes—the C/A code (coarse acquisition code) and the P code (precise code). The C/A code is broadcast on the L1 carrier frequency and is the information that civilian receivers can pick up. The P code is broadcast on the L1 and L2 carrier frequencies and contains more precise information, but a military receiver is required to pick up this signal. The Y code is an encrypted version of the P code and is used to prevent false P code information from being sent to a receiver by hostile forces. This “anti-spoofing” technique is commonly used to make sure that only the correct data is being received. Basically, the satellites are transmitting information in the codes about the location of the satellite, and they can also be used to determine the time when the signal was sent. By using this data, the receiver can find its position relative to that one satellite.

The signals are transmitted from space using high-frequency radio waves (the L1 and L2 carrier frequencies). These radio waves are forms of electromagnetic energy (to be discussed in Chapter 10) and will therefore be moving at the speed of light. Your receiver can compute the time it took for the signal to arrive from the satellite. If you know these high-frequency radio waves move at the speed of light (c), and you also know how long the transmission time (t) was, then you can calculate the distance between you and that one satellite by multiplying t by c. This result will give you the pseudorange (or distance) between your receiver and the satellite transmitting the signal.

Unfortunately, this still doesn’t tell us much—you know where you are on the ground in relation to the position of one satellite over 12,000 miles away, but that by itself gives you very little information about where you are on Earth’s surface. It’s like waking up in an unknown location and being told by a passerby that you’re 500 miles from Boston—it gives you very little to go on in determining your real-world location.

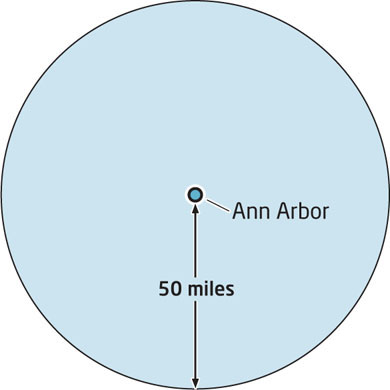
The process of determining your position is referred to as trilateration, which means using three points of reference to find where you are. Trilateration in two dimensions is commonly used when plotting a location on a map. Let’s say for example that you’re on a road trip to Michigan—you’ve been driving all night, and you’ve arrived in an unknown location with no identifying information to tell you where you are. The first person you bump into tells you (somewhat unhelpfully) that you’re 50 miles away from Ann Arbor, Michigan (see Figure 4.3). That puts you somewhere on a circle with Ann Arbor at its center 50 miles away, and gives you a choice of far too many possibilities to be of any use to you.

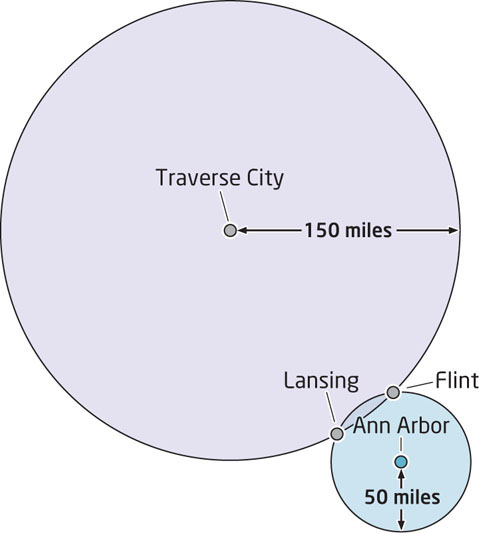
The second person you run into tells you (again, not being overly helpful) that you’re located 150 miles away from Traverse City, Michigan. This again puts your location somewhere on a circle 150 miles from Traverse City—but when you combine this with the information that places you 50 miles away from Ann Arbor, you can limit your options down considerably. There are only two cities in Michigan that are 50 miles from Ann Arbor and 150 miles away from Traverse City—you’re either in Lansing or Flint (Figure 4.4).

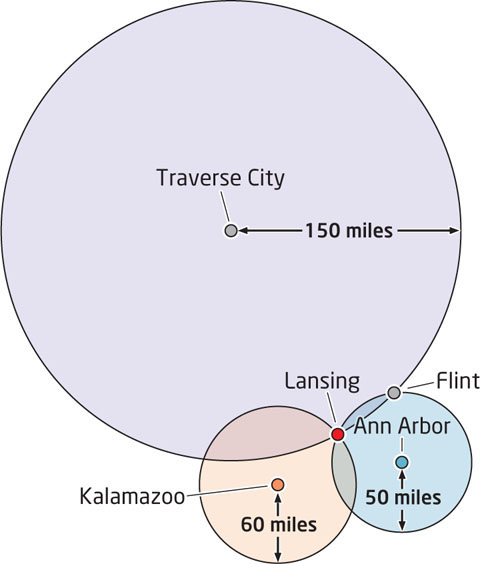
Luckily, the third person you see tells you that you’re 60 miles from Kalamazoo. Your first thought should be “Who are all these geographicallyminded people I keep running into?” while your second thought is that you now know exactly where you are. Lansing is the only option that fits all three of the distances from your reference points, so you can disregard Flint and be satisfied that you’ve found your location (see Figure 4.5 and Hands-on Application 4.1: Trilateration Concepts).

The same concept applies to finding your location using GPS, but rather than locating yourself relative to three other points on a map, your GPS receiver is finding its position on Earth’s surface relative to three satellites. Also, since a position on the three-dimensional (3D) Earth is being found with reference to positions surrounding it, a spherical distance is calculated rather than a flat circular distance. This process is referred to as trilateration in three dimensions (or 3D trilateration). The concept is similar, though finding the receiver’s position relative to one satellite means it’s located somewhere on one sphere (similar to only having the information about being 50 miles from Ann Arbor). By finding its location in relation to two satellites, the receiver is finding a location on a common boundary between two spheres. Finally, by finding the location relative to three satellites, there are only two places where those three spheres intersect, and the way the geometry works out, one of them is in outer space, and can be disregarded. That leaves only one location where all three spheres intersect, and thus one location on Earth’s surface relative to all three satellites. That position will be the location of the GPS receiver (Figure 4.6).

There’s just one problem with all this—and it’s serious. Remember, what you’re calculating is a pseudorange, based on the speed of light (which is a constant) and the time it takes for the signal to transmit from space to Earth. If that time is just slightly off, a different value for distance will be calculated, and your receiver will be located somewhere different from where it really is. This becomes an even bigger issue because the satellite has a super-precise and very expensive atomic clock (somewhere in the tens of thousands of dollars range), while the off-the-shelf GPS receiver has a less precise (and very much less expensive) quartz clock. Obviously, GPS receivers can’t have atomic clocks in them, because they’d be far too expensive to buy. Inevitably, the receiver’s clock isn’t going to be as accurate as the atomic clock, and timing errors can cause inaccuracies in calculating distances when it comes to finding a position. Fortunately, there’s an easy solution to this mess: your receiver picks up additional information from a fourth satellite. By using a fourth measurement, clock errors can be corrected and your position can be accurately determined. The position you’ll receive will be measured using the WGS84 datum.