Acquisition of Academic Skills: Reading, Writing, and Mathematics

One important goal to which children apply their intelligence is learning the skills and concepts taught at school. Because these skills and concepts are necessary for normal intellectual development in modern societies, because they are central to success in adulthood, and because they can be difficult to master, children spend more than 2000 days in school from 1st through 12th grade. Much of this time is devoted to acquiring proficiency in reading, writing, and mathematics. In this section, we focus on how children learn these skills, why some children have such difficulty mastering them, and how children’s learning can be improved.

Reading

Many children learn to read effortlessly, but others do not. You can no doubt remember the painful times classmates—and perhaps you, yourself—seemed to take forever to read aloud simple sentences, even in 2nd and 3rd grade. Why is it that some children learn to read so easily, whereas others experience great difficulty and frustration? To answer this question, we must examine the typical path of reading development as well as how and why children deviate from it.

Chall (1979) described five stages of reading development. These stages provide a good overview of the typical path to mastery:

• 1. Stage 0 (birth until the beginning of 1st grade): During this time, many children acquire key prerequisites for reading. These include knowing the letters of the alphabet and gaining phonemic awareness, that is, knowledge of the individual sounds within words.
  
• 2. Stage 1 (1st and 2nd grades): Children acquire phonological recoding skills, the ability to translate letters into sounds and to blend the sounds into words (informally referred to as “sounding out”).
  

  phonological recoding skills ability to translate letters into sounds and to blend sounds into words; informally called sounding out

• 3. Stage 2 (2nd and 3rd grades): Children gain fluency in reading simple material.
• 4. Stage 3 (4th through 8th grades): Children become able to acquire reasonably complex, new information from written text. To quote Chall, “In the primary grades, children learn to read; in the higher grades, they read to learn” (1979, p. 24).
• 5. Stage 4 (8th through 12th grades): Adolescents acquire skill not only in understanding information presented from a single perspective but also in coordinating multiple perspectives. This ability enables them to appreciate the subtleties in sophisticated novels and plays, which almost always include multiple viewpoints.

This description of developmental stages provides a general sense of the reading acquisition process and a framework for understanding how particular developments fit into the broader picture.

Prereading Skills

Preschoolers acquire certain basic information about reading just from looking at books and having their parents read to them. They learn that (in English and other European languages) text is read from left to right; that after they reach the right end of a line, the text continues at the extreme left of the line below; and that words are separated by small spaces.

Children with well-educated parents also tend to learn the names of most or all the letters of the alphabet before they enter school. This tends not to be true of children whose parents are poorly educated. In one study of beginning kindergartners, 86% of children whose mothers graduated from college were proficient in letter recognition, but only 38% of children whose mothers did not complete high school were (J. West, Denton, & Germino-Hausken, 2000).

Kindergartners’ mastery of letter names is positively correlated with their later reading achievement through at least 7th grade (Vellutino & Scanlon, 1987). However, no causal relation exists between the two: teaching the names of the letters to randomly chosen preschoolers does not increase their subsequent reading achievement (Piasta & Wagner, 2010). Instead, it appears that other variables, such as children’s interest in books and parents’ interest in their children’s reading, stimulate both early knowledge of the alphabet and later high reading achievement.

The appeal of nursery rhymes to young children has always been obvious, but only recently have the benefits of such rhymes for phonemic awareness and reading acquisition become known.

JOHN Y CRAWFORD/THE IMAGE WORKS

Phonemic awareness, on the other hand, is both correlated with later reading achievement and a cause of it. To measure awareness of the component sounds within words, researchers ask children to decide whether two words start with the same sound, to identify component sounds within a word, and to indicate what would remain if a given sound were removed from a word. Kindergartners’ performance on these measures of phonemic awareness is the strongest predictor of their ability to sound out and spell words in the early grades—stronger even than IQ score or social-class background (Nation, 2008; Rayner et al., 2001)—and it continues to be related to reading achievement as much as 11 years later, above and beyond the influence of the child’s social-class background (MacDonald & Cornwall, 1995).

Even more impressive, a review of 52 well-controlled experimental studies indicated that teaching phonemic-awareness skills to 4- and 5-year-olds causes them to become better readers and spellers, with the effects enduring for years after the training (National Reading Panel, 2000). Instructing young children to break words into their component sounds and then writing the letter that best matches each successive sound causes especially large gains in spelling (Levin & Aram, 2013).

Although explicit training can help foster phonemic awareness, most children do not receive such training. Where, then, does phonemic awareness come from in the natural environment? One relevant experience is hearing nursery rhymes. Many nursery rhymes highlight the contribution of individual sounds to differences among words (e.g., “I do not like green eggs and ham; I do not like them, Sam I am.”) Consistent with this hypothesis, 3-year-olds’ knowledge of nursery rhymes correlates positively with their later phonemic awareness, above and beyond their IQ scores and their mother’s educational level (Maclean, Bryant, & Bradley, 1987). Other factors that contribute to the development of phonemic awareness include growth of working memory, increasingly efficient processing of language, and, especially, reading itself (Anthony & Francis, 2005; McBride-Chang, 2004). Children with greater phonemic awareness read more and read better, which, in turn, leads to further increases in their phonemic awareness and in the quantity and quality of their reading.

Word Identification

Rapid, effortless word identification is crucial not only to reading comprehension but also to its enjoyment. One remarkable finding makes the point: 40% of 4th-graders who were poor at identifying words said they would rather clean their rooms than read (Juel, 1988). One child went as far as to volunteer, “I’d rather clean the mold around the bathtub than read.” Thus, not only does poor word identification make the reading process slow and laborious, it also leads children to read no more than is absolutely necessary, which, in turn, hinders improvement in their reading skills.

Words can be identified in two main ways: phonological recoding and visually based retrieval. As previously indicated, phonological recoding involves converting the visual form of a word into a verbal, speechlike form and using the speechlike form to determine the word’s meaning. Visually based retrieval involves processing a word’s meaning directly from its visual form.

Most young children use both approaches (Share, 2004), choosing adaptively between them from 1st grade onward. They do so through a strategy-choice process, in which they choose the fastest approach that is likely to allow correct word identification. In the context of reading, this means that on easy words, children rely heavily on the fast but not always accurate approach of visually based retrieval; on hard words, they resort to the slower but surer strategy of phonological recoding. As shown in Figure 8.10, 1st-graders are very skillful in adjusting their strategies to the difficulty of a particular word.

FIGURE 8.10 Young children’s strategy choices in reading A strong positive correlation exists between the difficulty of a word, as defined by the percentage of errors children make on it, and the frequency of young children’s use of an overt strategy, such as audible phonological recoding, to read it. Thus, on words that 1st-graders find easy, such as “in,” they generally retrieve the word’s pronunciation, but on words they find difficult, such as “parade,” they often fall back on overt strategies such as sounding out. (Siegler, 1986)

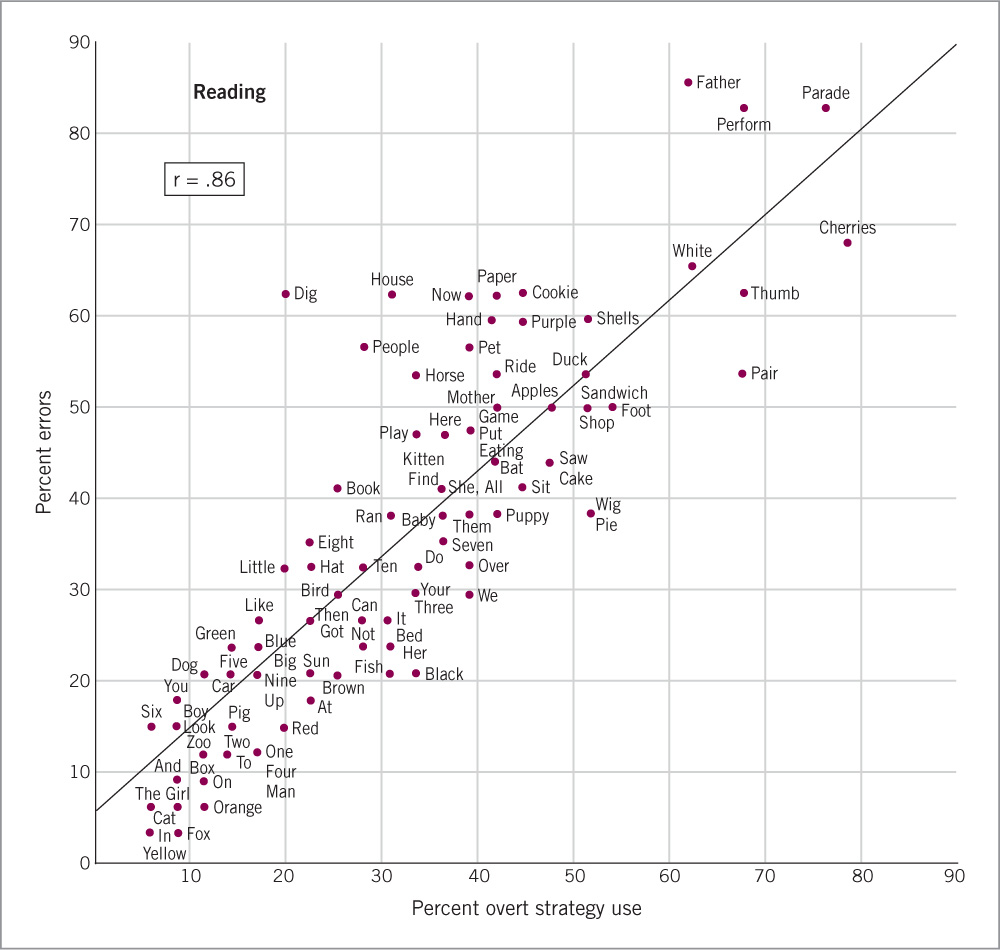
The mechanisms underlying this adaptive strategy choice involve a form of associative learning in which children’s past behavior shapes their future behavior (Siegler, 1996). Beginning readers rely heavily on phonological recoding, because the associations between words’ visual forms and their sounds are too weak to allow much use of retrieval. Correct use of phonological recoding increases the associations between words’ visual forms and their sounds, which in turn allows greater use of visually based retrieval. Consistent with this view, the shift to retrieval occurs most rapidly for words on which children most often execute phonological recoding correctly—words that are short, that have regular letter–sound relations, and that children encounter frequently. Also consistent with this view, children who are better at phonological recoding stop using that approach earlier, because their past success with it enables them to shift more rapidly to visually based retrieval. A third correct implication is that reading instruction that emphasizes phonics, and the strategy of phonological recoding, should help to produce fast and accurate word identification (M. J. Adams, Treiman, & Pressley, 1998; Xue & Meisels, 2004).

With age and experience, vocabulary knowledge becomes an increasingly important influence on word identification, particularly on words with irregular sound–symbol correspondences (Nation, 2008). However, phonological recoding skill also continues to be important, even for adults when they encounter unfamiliar words. Box 8.3 discusses the relation between poor phonological recoding skills and the reading disability known as dyslexia.

Comprehension

The point of learning to read individual words is to comprehend the text in which the words appear. Reading comprehension involves forming a mental model to represent the situation or idea being depicted in the text and continuously updating it as new information appears (Oakhill & Cain, 2000). All the types of mental operations that influence cognitive development in general—basic processes, strategies, metacognition (knowledge about people’s thinking), and content knowledge—also influence the development of reading comprehension.

Basic processes such as encoding (identification of key features of an object or event) and automatization (executing a process with minimal demands on cognitive resources) are crucial to reading comprehension. The reason is simple: children who are able to identify the key features of stories will understand the story better, and children who are able to automatically identify the key features of words will have more cognitive resources left to devote to comprehension. Fast, accurate word identification correlates positively with reading comprehension at all points from the 1st grade through adulthood (Cunningham & Stanovich, 1997).

Box 8.3: individual differences: Dyslexia

dyslexia inability to read and spell well despite having normal intelligence

Some children of normal intelligence whose parents encourage reading nonetheless read very poorly. Such poor reading despite normal intelligence is referred to as dyslexia and affects 5% to 10% of children in the United States (Anthony & Francis, 2005). The causes of dyslexia are not well understood, but genetics are clearly part of the story. If one of a pair of monozygotic twins is diagnosed as dyslexic, the probability of the other twin receiving a similar diagnosis is 84%, whereas if the twins are dizygotic, the corresponding probability is 48% (Kovas & Plomin, 2007; Oliver et al., 2004). The extent of genetic influences varies with parental educational level: as with IQ score, genetic influences on dyslexia are larger with children of highly educated parents than with children of less educated parents (Friend, DeFries, & Olson, 2008).

At a cognitive level of analysis, dyslexia stems primarily from weak ability to discriminate between phonemes, from poor short-term memory for verbal material (as indicated, for example, by poor ability to recall an arbitrary list of words), and from slow recall of the names of objects (Vellutino, Scanlon, & Spearing, 1995; Wimmer, Mayringer, & Raberger, 1999). Determining the sounds that go with vowels is especially difficult for children with dyslexia, at least in English, where a single vowel can be pronounced in many ways (consider the sounds that accompany the letter “a” in “ha,” “hat,” “hall,” and “hate.” “Because of these weaknesses, dyslexic children have great difficulty mastering the letter–sound correspondences used in phonological recoding, especially in languages, such as English, with irregular sound–symbol correspondences (Sprenger-Charolles, 2004).

This chart shows the number of pseudowords identified correctly by 7- to 14-year-olds with and without reading disabilities. Note that 13- and 14-year-olds with reading disabilities correctly identified no more items than did typical 7- and 8-year-olds. The poor phonological recoding skills of children with reading disabilities lead them to have special difficulty with pseudowords that, because they are totally unfamiliar, can be pronounced only by using phonological recoding. (Data from Siegel, 1993)

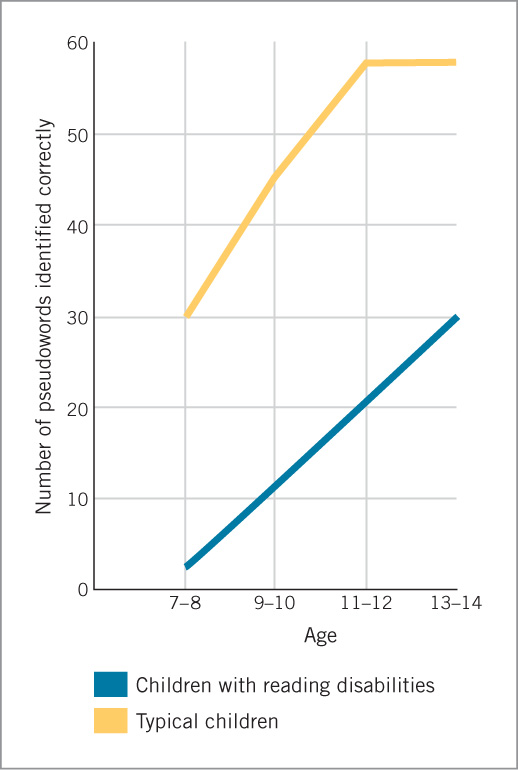
For instance, as shown in the figure, when asked to read pseudowords such as parding, dyslexic 13- and 14-year-olds perform at the same level as typical 7- and 8-year-olds (Siegel, 1993). As would be expected from the strategy–choice model described on page 324, this difficulty with phonological processing causes most dyslexic children to be poor at visually based retrieval, as well as at sounding out words (Manis et al., 1996).

The problem can be a lasting one: most individuals who have poor phonological processing skills in early elementary school remain poor readers as adults (Wagner et al., 1997). This is especially the case for children who are from disadvantaged backgrounds and who attend inferior schools: children with dyslexia who come from more advantaged family backgrounds and who attend better schools are more likely to show substantial improvements (S. E. Shaywitz, Mody, & Shaywitz, 2006).

Studies of brain functioning support the view that poor phonological processing is at the heart of dyslexia. When dyslexic children read, two areas of their brains are less active than the corresponding areas in typical children reading the same words (Schlaggar & Church, 2009; Tanaka et al., 2011). One such area is directly involved in discriminating phonemes; the other area is involved in integrating visual and auditory data (in this case, integrating letters on the page with accompanying sounds).

How can dyslexic children be helped? One tempting idea is that because these children have difficulty learning phonics, they would learn better through an approach that deemphasizes letter–sound relations and instead emphasizes either visually based retrieval or reliance on context. These alternative methods work poorly, however (Lyon, 1995); there is simply no substitute for being able to sound out unfamiliar words. Indeed, what seems to work best is to teach children with dyslexia to use strategies that enhance their phonological recoding (Lovett et al., 1994). Effective strategies include drawing analogies to known words with similar spellings; generating alternative pronunciations of vowels when the first attempt at sounding out does not yield a plausible word; and, with long words, “peeling off” prefixes and suffixes and then trying to identify the rest of the word. Using such strategies helps children with dyslexia to improve their reading-achievement scores (Lovett et al., 1994).

Development of reading comprehension is also aided by acquisition of reading strategies. For example, good readers proceed slowly when they need to master written material in depth and speed up when they need only a rough sense of it (Pressley & Hilden, 2006). Proficiency in making such adjustments develops surprisingly late. Even when 10-year-olds are told that some material is crucial and other material is not, they tend to read all the material at the same speed. In contrast, 14-year-olds skim the nonessential parts and spend more time on the important ones (Kobasigawa, Ransom, & Holland, 1980).

Increasing metacognitive knowledge also contributes to improved reading comprehension. With age and experience, readers increasingly monitor their ongoing understanding and reread passages they do not understand (Nicholson, 1999). Such comprehension monitoring differentiates good readers from poor ones at all ages from 1st grade through adulthood. Instructional approaches that focus on comprehension monitoring and other metacognitive skills, such as anticipating questions that a teacher might ask about the material, improve reading comprehension (Palincsar & Magnusson, 2001; Rosenshine & Meister, 1994).

Another powerful influence on the development of reading comprehension is increasing content knowledge. Relevant content knowledge frees cognitive resources for focusing on what is new or complex in the text and allows readers to draw reasonable inferences about information left unstated. Thus, when reading the headline “Pirates Maul Giants,” readers knowledgeable about baseball realize that the headline concerns a baseball game; it is unclear how readers who lack baseball knowledge would interpret such a headline.

The path to strong or weak reading comprehension begins even before children start school. Hearing stories told or read by their parents helps preschoolers learn how such stories tend to go, facilitating their understanding of new stories once they read themselves. It also enhances their general level of language development (Raikes et al., 2006; Whitehurst & Lonigan, 1998). The amount that parents read to their children during the preschool years also partially accounts for the differences between the reading comprehension skills of children from middle- and low-income families. For example, a study conducted in Israel showed that in an affluent school district with high reading-achievement scores, 96% of parents of preschoolers read to them daily. The same was true of only 15% of parents of preschoolers in a poor district with low scores (Feitelson & Goldstein, 1986).

The straightforward implication of these findings is that if preschoolers from poor families were read to daily, they too would become better readers. The evidence is consistent with this inference. Encouraging low-income parents to also actively engage their children in the reading process, such as by asking them to relate what is being read to their own experiences or to explain the characters’ goals and motivations, helps even more (Zevenbergen & Whitehurst, 2003). Persuading low-income parents to enroll in such programs and read to their children on a continuing basis is not easy, because of time demands and, in many cases, the pressures of being a single parent (Whitehurst et al., 1999); but when parents do so, their children’s reading comprehension benefits.

Once children enter school, the amount of material they read varies greatly and has a large effect on their reading comprehension. For instance, U.S. 5th-graders whose reading-achievement test scores are in the 90th percentile for their grade report roughly 200 times as much discretionary reading as peers who score in the 10th percentile (Anderson, Wilson, & Fielding, 1988). High reading ability leads children to read more; children who read more, in turn, show greater gains over time in reading comprehension than do children of equal ability who read less (Guthrie et al., 1999).

Individual Differences

Individual differences in reading ability tend to be stable over time. Children who have relatively advanced reading skills when they enter kindergarten tend to be better readers through elementary, middle, and high school (Duncan et al., 2007; Harlaar, Dale, & Plomin, 2007). Studies of adoptive and nonadoptive siblings and of monozygotic and dizygotic twins indicate that these continuities of individual differences reflect both shared genes and shared environments (Petrill et al., 2007; Wadsworth et al., 2006). As we have noted, genetic and environmental influences are mutually reinforcing: parents who are good and frequent readers are likely to provide both genes and environments that make it likely that their children will be relatively good readers when they are young, which makes it more likely that the children will seek out reading opportunities, which will further improve their reading, and so on (Petrill et al., 2005).

Writing

Much less is known about the development of children’s writing than about the development of their reading, but what is known shows interesting parallels between the two.

Prewriting Skills

FIGURE 8.11 A 3½-year-old’s effort at writing The child’s symbols, although unconventional, indicate an understanding that words require separate symbols.

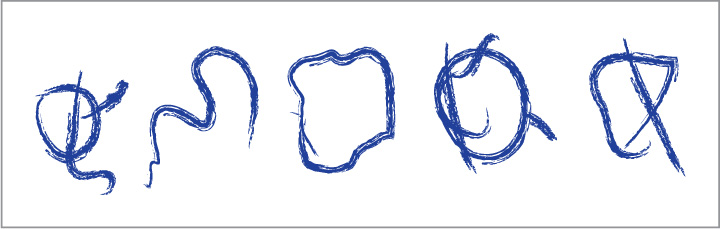
The development of writing, like the development of reading, begins before children receive formal schooling. Figure 8.11 displays writing efforts typical of a 3½-year-old. The marks are not conventional letters of the alphabet, but they look vaguely like them and are arranged along a roughly horizontal line. By age 4, children’s “writing” is sufficiently advanced that adults have no trouble distinguishing it from the figures 4-year-olds produce when asked to draw a flower or a house (Tolchnisky, 2003).

Preschoolers’ “writing” indicates that they expect meaning to be reflected in print. They use more marks to represent words that signify many objects, such as “forest,” than to represent words that signify a single object, such as “tree” (Levin & Korat, 1993). Similarly, when asked to guess which of several words is the name for a particular object, they generally choose longer words for larger objects (Bialystok, 2000). Although written language does not work this way, the children’s guess seems reasonable.

Generating Written Text

FIGURE 8.12 A 4th-grader’s story The intended title of this story was The Kid Who Lost Things. See if you can figure out the rest. (From Berninger & Richards, 2002)

ELSEVIER

Learning to write, in the sense of writing an essay or story, is a good deal more difficult than learning to read. This is not surprising, because writing requires focusing simultaneously on numerous goals, both low level and high level. The low-level goals include forming letters, spelling words, and using correct capitalization and punctuation. The high-level goals include making arguments comprehensible without the intonations and gestures that help us communicate when we speak, organizing individual points in a coherent framework, and providing the background information that readers need to understand the writing (Berninger & Richards, 2002). The difficulties children have in meeting both the low-level and high-level goals result in their often writing the type of flat story illustrated in Figure 8.12.

As with development of reading comprehension, growth of writing proficiency reflects improvements in basic processes, strategies, metacognition, and content knowledge. Automatizing low-level skills, such as spelling and punctuation, aids writing not only because correct spelling and punctuation make writing easier to understand but also because automatizing the low-level skills frees cognitive resources for pursuing the higher-level communicative goals of writing. Consistent with this conclusion, children’s proficiency at low-level skills such as spelling correlates positively with the quality of the children’s essays (Juel, 1994).

Acquisition of strategies also contributes to improvements in writing. One common strategy is to sequence high-level goals in a standard organization, or script, a set of actions or events that occurs repeatedly. Harriet Waters, a psychologist whose proud mother saved all her daughter’s “class news” assignments from 2nd grade, was one child who employed such an approach (Waters, 1980). As shown in Table 8.4, in each class news essay, Waters first noted the date, then described the weather, and then discussed events of the school day—a strategy that greatly simplified her writing task. For older children, formulating outlines serves a similar purpose of dividing the task of writing into manageable parts: first figure out what you want to say, then figure out the best order for making your main points, then figure out how to make each point.

Metacognitive understanding plays several crucial roles in writing. Perhaps the most basic type of metacognitive understanding is recognizing that readers may not have the same knowledge as the writer and that one therefore should include all the information that readers will need to allow them to grasp what is being said. Good writers consistently exhibit such understanding by high school; poor writers often do not (Berninger & Richards, 2002). A second crucial type of metacognitive knowledge involves understanding the need to plan one’s writing rather than just jumping in and starting to write. Good writers spend much more time than do poor writers planning what they will say before they begin writing—making notes, constructing outlines, and so on (Kellogg, 1994). Understanding the need for revision is a third key type of metacognitive knowledge. Good writers spend more time revising their already relatively good first drafts than poor writers spend revising their poorer ones (Fitzgerald, 1992).

Fortunately, as with reading, instruction aimed at inculcating metacognitive understanding can enhance writing skills (S. Graham & Harris, 1996). In particular, the writing of both typical and learning-disabled children improves when they are taught to revise other children’s work and to ask themselves several basic questions: Who is the main character in this story? What does the main character do? How do the other characters respond? How does the main character respond to the other characters’ responses? What happens in the end? Asking children to reflect on the relative quality of essays written by other children and on why some essays are better than others also can improve writing (Braaksma et al., 2004).

Finally, as in reading, content knowledge plays a crucial role in writing. Children generally write better when they are familiar with the topic than when they are not (Bereiter & Scardamalia, 1982). Thus, the standard advice “Write what you know” applies to children as well as to aspiring authors.

Mathematics

In Chapter 7, we examined infants’ early-developing nonverbal number sense and the emergence of counting between ages 2 and 4 years. Here we examine the development of arithmetic, which builds on both types of knowledge.

Arithmetic

People often think of arithmetic learning as a process of rote memorization, but it actually is far more complex and interesting. How well children learn arithmetic depends on the strategies that they use, the precision of their representations of numerical magnitudes, and their understanding of basic mathematical concepts and principles.

Strategies From age 4 or 5 years, when most children begin to learn arithmetic, they use a variety of problem-solving strategies. The most common initial strategies are counting from 1 (e.g., solving 2 + 2 by putting up two fingers on each hand and counting “1, 2, 3, 4”) and retrieval (recalling answers from memory). At first, children can use these strategies only to answer a few simple problems, such as 1 + 2 and 2 + 2, but they gradually expand their use to a wider range of single-digit problems (Geary, 2006).

Learning arithmetic is harder than it looks.

© BIL KEANE, INC./KING FEATURES SYNDICATE

When children begin to do arithmetic on a daily basis, in kindergarten or first grade, they add several new strategies. One is counting from the larger addend (e.g., solving 3 + 9 by counting, “9, 10, 11, 12”). Another fairly common strategy is decomposition, which involves dividing a problem into two easier ones (e.g., solving 3 + 9 by thinking “3 + 10 = 13; 13 − 1 = 12”). Children continue to use the earlier developing strategies as well; most 1st-graders use three or more strategies to add single-digit numbers (Siegler, 1987).

Similarly varied strategy use is present on all four arithmetic operations. For example, to solve a multiplication problem such as 3 × 4, children sometimes write three 4s and add them, sometimes make three bundles of four hatch marks and count them, and sometimes retrieve 12 from memory (Mabbott & Bisanz, 2003). Use of these arithmetic strategies is surprisingly enduring: even college students use strategies other than retrieval on 15% to 30% of single-digit problems (LeFevre et al., 1996; Lemaire, 2010).

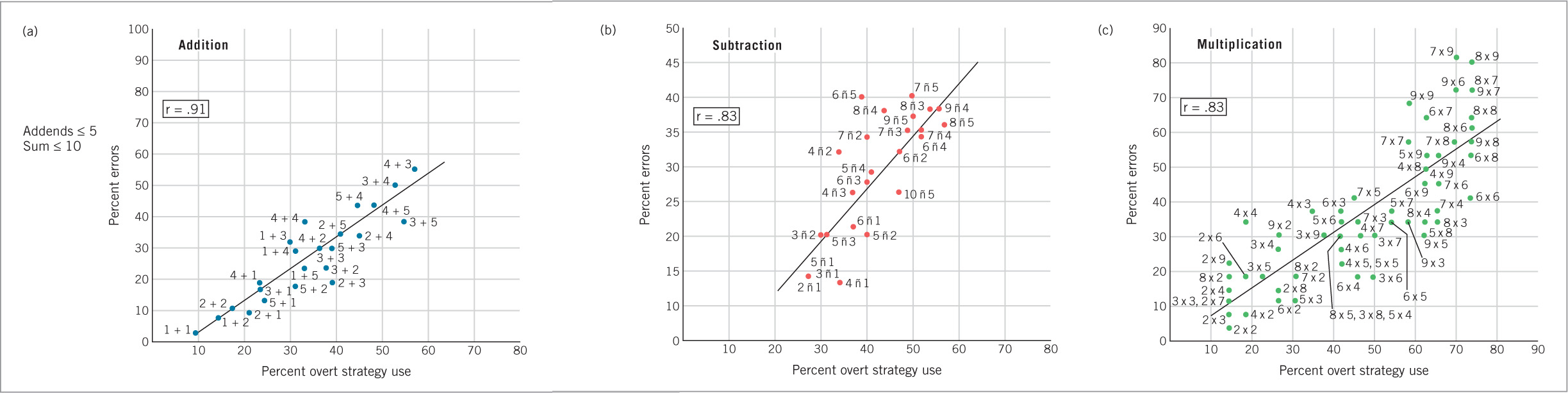
Just as children’s choices among word-identification strategies are highly adaptive, so are their choices among arithmetic strategies (Siegler, 1996). Even 4-year-olds choose in sensible ways, usually solving easy problems such as 2 1 2 quickly and accurately by using retrieval and usually solving harder problems such as 5 1 2 less quickly but still accurately by counting from 1 (Figure 8.13). As children gain experience with the answers to single-digit arithmetic problems, their strategy choices shift increasingly toward using retrieval of those answers. The learning process seems to be the same as with the corresponding shift toward visually based retrieval in reading. The more often children generate the correct answer to a problem, regardless of the strategy they use to generate it, the more often they will be able to retrieve that answer, thereby avoiding the need to use slower counting strategies.

FIGURE 8.13 Young children’s strategy choices in (a) addition, (b) subtraction, and (c) multiplication As illustrated previously with reading (Figure 8.10), a strong positive correlation exists between the difficulty of a problem, as defined by the percentage of errors it elicits, and the frequency of using an overt strategy, such as counting on one’s fingers. Thus, for problems that 4- and 5-year-olds found easy, such as 2 + 2, they usually used retrieval. For problems they found difficult, such as 4 + 3, they usually used overt strategies, such as counting from 1. (Siegler, 1986)

Understanding numerical magnitudes Numerical magnitude representations are mental models of the way quantities are ordered along a less-to-more dimension. Regardless of whether “7” refers to a distance (7 inches), a weight (7 pounds), a duration (7 hours), or a set size (7 people), the magnitude represented by “7” is larger than that indicated by “6”—and smaller than that indicated by “8”—of the same unit.

The idea that symbolically expressed numbers represent magnitudes might seem obvious, but accurately linking such numbers and the magnitudes they represent actually constitutes a major challenge over a prolonged period of development. Here are some examples: many preschoolers who can count flawlessly from 1 to 10 do not know whether 4 or 8 indicates the greater number of objects (Le Corre & Carey, 2007); many elementary school children estimate the location of 150 as being near the midpoint of a number line with 0 and 1000 at the two ends (Siegler & Opfer, 2003); many adolescents and adults have no idea whether 3/5 is larger or smaller than 5/11 (Meert, Grégoire, & Noël, 2010). What is lacking in all these cases is accurate representations of numerical magnitudes.

Understanding symbolic numerical magnitudes is closely related to understanding arithmetic and indeed to mathematics achievement in general. This relation is evident in arithmetic errors, whose magnitudes usually are close to the correct answer (8 × 7 = 54) rather than far from it (8 × 7 = 24). Similarly, when asked whether answers to arithmetic problems are correct, both children and adults identify incorrect answers more quickly when the magnitude of error is considerable (8 + 4 = 18) than when it is small (8 + 4 = 14) (Ashcraft, 1982; Siegler, 1988).

The range of numbers whose magnitudes children represent reasonably precisely, as indicated by the accuracy of their magnitude comparisons and number-line estimates, changes greatly with age and experience (Figure 8.14). Accuracy of magnitude representations of the numbers 1–10 increases greatly between ages 3 and 6 (Bertelletti et al., 2010); that of numbers 1–100, between ages 6 and 8 (Geary et al., 2007); that of numbers 1–1000, between ages 8 and 12 (Siegler & Opfer, 2003); and so on.

FIGURE 8.14 The number-line task and typical developmental changes on it (a) On each trial with a 0–100 number line, children need to estimate a different number’s location on the line. (b) Kindergartners’ median estimates for each number on the 0–100 number-line task increased with the number being estimated, but in a way that involved overestimates of relatively small numbers and underestimates of large ones, as with a logarithmic function. (c) Second-graders’ median estimates for each number on the same task increased linearly with the size of the number being estimated, and were quite accurate. (Data from Siegler & Booth, 2004)

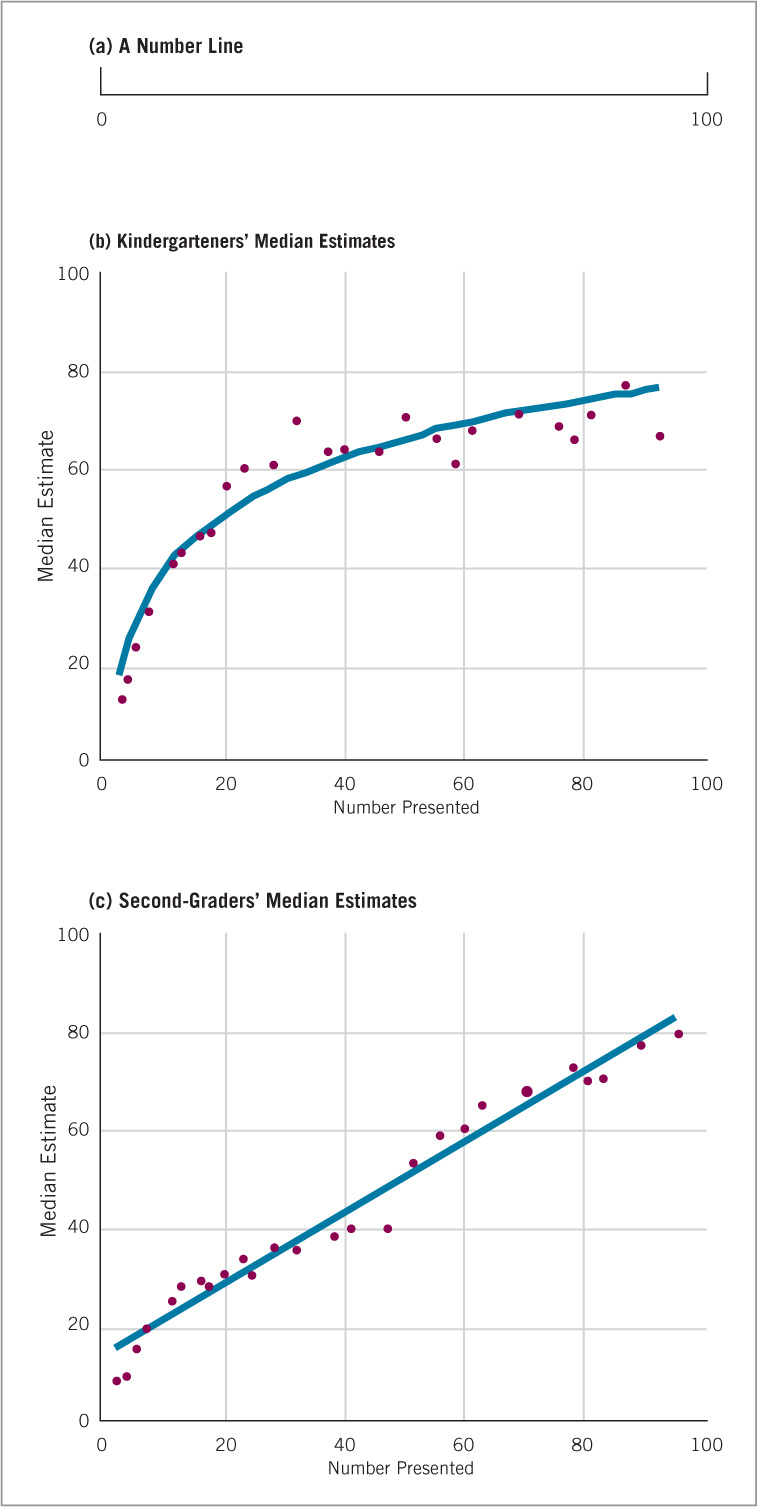
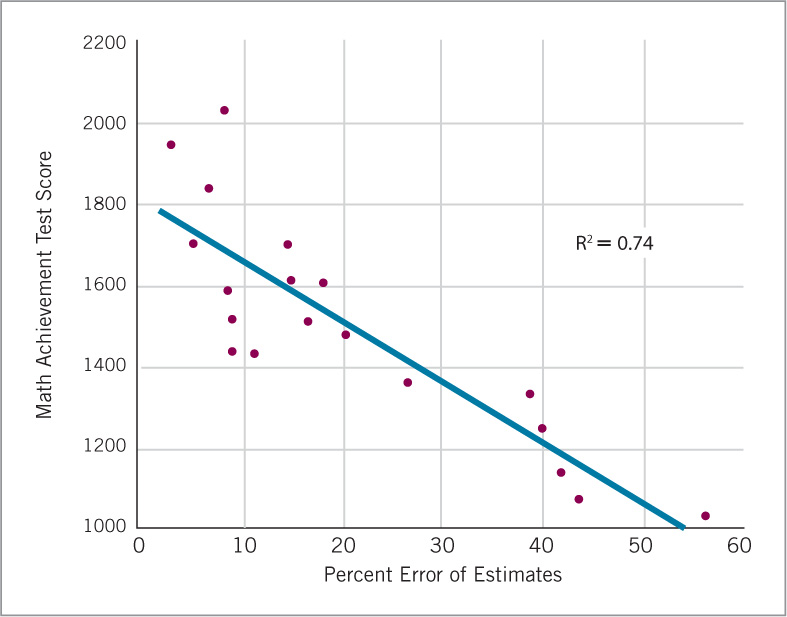
Children of any given age differ considerably in their knowledge of numerical magnitudes. These differences are related to the children’s overall mathematical knowledge. During elementary school, children who more accurately estimate whole-number magnitudes on number lines have higher math achievement. During middle school, the same is true for children who accurately estimate fraction magnitudes (Figure 8.15) (D. H. Bailey et al., 2012; Jordan et al., 2013; Siegler & Pyke, 2013).

FIGURE 8.15 Relation between 8th-graders’ number-line estimation accuracy and their math achievement test scores Accuracy of number-line estimation is closely related to overall mathematics achievement. These data show the relation between middle school children’s math achievement test scores and the accuracy of their estimates of fraction magnitudes. Similar relations have been found between elementary school children’s math achievement test scores and their estimates of whole-number magnitudes. The correlation is negative, because estimates that are less distant from numbers’ correct locations indicate greater knowledge of the numerical magnitudes. (Data from Siegler, Thompson, & Schneider, 2011)

Part of the reason for this relation is that more accurate magnitude representations help children learn arithmetic. The more precisely a child understands numerical magnitudes, as measured by his or her accuracy in estimating the position of numbers on a number line, the greater the child’s arithmetic proficiency (J. L. Booth & Siegler, 2006; 2008; Geary et al., 2007). Moreover, instruction that improves the accuracy of children’s symbolic numerical magnitude representations also improves their subsequent learning of arithmetic (J. L. Booth & Siegler, 2008; L. S. Fuchs et al., 2013; Siegler & Ramani, 2009). Accurate magnitude representations may enhance arithmetic learning by suggesting plausible answers and eliminating implausible ones from consideration.

Conceptual understanding of arithmetic Understanding why some arithmetic procedures are appropriate and others inappropriate poses a major challenge for many children, even those who have memorized the correct procedure. Such conceptual understanding of arithmetic begins developing during the preschool period; for example, many 4-year-olds understand the commutative law of addition, the principle that adding a + b is the same as adding b + a (Canobi, Reeve, & Pattison, 2002). Not until years later, however, do they master more advanced arithmetic concepts, such as mathematical equality—the idea that the values on the two sides of the equal sign must balance. On almost all problems in which young children encounter the equal sign, numbers appear only to the left of it (e.g., 3 + 4 = __; 3 + 4 + = 5 __). For purposes of solving such problems, children can interpret the equal sign merely as a signal to start adding.

Eventually, however, children encounter arithmetic problems with numbers on both sides of the equal sign, such as 3 + 4 + 5 = __ + 5. As late as 4th grade, most children in the United States answer such problems incorrectly (Goldin-Meadow, Cook, & Mitchell, 2009). The most common incorrect approach is to add all the numbers to the left of the equal sign, which in the above problem sum to 12, and to assume that this sum is the answer to the problem. Such errors reflect not only a lack of understanding that the equal sign means that the values on both sides of it must be equivalent but also interference from the vast amount of practice children have had solving typical addition problems, which have no number following the equal sign (McNeil et al., 2011).

In many cases, children’s hand gestures reveal that they have somewhat better understanding of mathematical equality than is revealed by their answers or explanations. For example, on the problem 3 + 4 + 5 = __ + 5, children often answer “12” and explain that they solved the problem by adding 3 + 4 + 5, but during their explanation, they point to all four numbers rather than just to the three preceding the equal sign. This pointing suggests an implicit recognition that the fourth number might be important, even though they did not include it in their calculation (Goldin-Meadow & Alibali, 2002). Children who initially show such gesture-speech mismatches, in which their gesturing conveys more information than their verbal statements, learn more from instruction on mathematical equality problems than do peers whose gesturing and speech before the instruction were consistent (that is, those who said “12” and pointed only to the three numbers preceding the equal sign).

The gestures play a causal role in learning as well: children who are encouraged to gesture appropriately while explaining answers to mathematical equality problems learn more than children encouraged not to gesture (Goldin-Meadow, Cook, & Mitchell, 2009). The positive relation between gesture–speech mismatches and subsequent learning has emerged on number conservation and physics problems as well as on mathematical equality problems. These findings illustrate a common conclusion: variability of thought and action (for example, generating diverging gestures and speech or advancing multiple explanations of a phenomenon rather than just one) often indicates heightened readiness to learn (Church, 1999; Siegler, 2006; Thelen & Smith, 2006).

Mathematics Anxiety

Many children experience mathematics anxiety, a negative emotional state that leads to fear and avoidance of math (Ashcraft & Ridley, 2005). Such anxiety can be evident as early as 1st grade (Ramirez et al., 2012) and for many people presents a lifelong problem. Mathematics evokes more anxiety than other school subjects, probably because of the unambiguous right/wrong status of answers to many mathematics problems, the widespread belief that mathematics is closely linked to intelligence, and the frustrating periods with no apparent progress that mathematics learning often entails.

Mathematics anxiety is considerably more prevalent in girls than in boys (Devine et al., 2012). It is correlated with poor mathematics achievement, but some people experience it despite having high mathematics achievement and not suffering from high anxiety in general (Ashcraft & Krause, 2007; Maloney & Beilock, 2012). The feelings of dread that math can inspire contribute to the negative outcomes that are feared; a likely reason is that the anxiety reduces the working memory resources needed to solve mathematics problems (Beilock & DeCaro, 2007). Consistent with this interpretation, when presented with mathematics tasks, people with math anxiety show both unusually great activity on the right side of the amygdala, a part of the brain involved in processing negative emotions, and depressed activity in brain areas crucial to working memory (C. B. Young, Wu, & Menon, 2012).

How do some children become anxious about math? The mechanisms are not well understood, but one contributor appears to be the views of adults who are important in the children’s lives. Parents and teachers who are themselves anxious about mathematics tend to convey their beliefs and feelings to their children. The problem seems to be especially great for girls whose parents and teachers are pessimistic about girls’ mathematical abilities (Beilock et al., 2010; Meece, Wigfield, & Eccles, 1990).

The negative impact of anxiety on mathematics learning has prompted efforts to find ways of reducing it. One promising intervention is surprisingly simple: have students write a brief description of their emotions just before taking a test. Such expressive writing reduces anxiety and boosts performance in a variety of areas in which negative emotions interfere with learning and performance, including mathematics (Ramirez & Beilock, 2011). Putting the negative thoughts on paper might help students think about the situation more objectively and thus allow them to concentrate on the math problems.

Even among children with mathematics anxiety, most learn the basics reasonably well. However, as noted in Box 8.4, the learning process goes seriously awry with certain children who suffer from the general difficulty in thinking about numbers that is known as mathematics disability.