15.1 Parameters and statistics
Our study of inference begins with populations that have some outcome of interest. For convenience, call the outcome we are looking for a “success.” In the college student survey, the population is all college freshmen, and a “success” is a student who would report that their emotional health was “above average.”
When using sample data to draw conclusions about a wider population, we must take care to keep straight whether a number describes a sample or a population. Here is the vocabulary we use.
WHO IS A SMOKER?
When estimating a proportion p, be sure you know what counts as a “success.” The news says that 20% of adolescents smoke. Shocking. It turns out that this is the percent who smoked at least once in the past month. If we say that a smoker is someone who smoked on at least 20 of the past 30 days and smoked at least half a pack on those days, fewer than 4% of adolescents qualify.
Parameter, Statistic
A parameter is a number that describes the population. In statistical practice, the value of a parameter is not known because we cannot examine the entire population.
A statistic is a number that can be computed from the sample data without making use of any unknown parameters. In practice, we often use a statistic to estimate an unknown parameter.
EXAMPLE 15.1: Risky Behavior in the Age of AIDS
How common is behavior that puts people at risk of AIDS? In the early 1990s, the landmark National AIDS Behavioral Surveys used random dialing of telephone numbers to contact a sample of 2673 adult heterosexuals. Of these, 170 had more than one sexual partner in the past year.2 The population that the survey wants to draw conclusions about is all heterosexual adults.
The parameter of interest is p, the proportion of all heterosexual adults who had more than one sexual partner in the last year. We don’t know the value of this parameter. The statistic that estimates the proportion of all adult heterosexuals having multiple sexual partners in the last year is the sample proportion
sample proportion
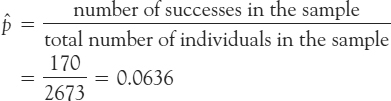
Read the sample proportion 
as “p-hat.” The proportion 0.0636 is a statistic because it describes this one sample. A different sample of 2673 heterosexual adults would almost certainly lead to a value of
that differs from 0.0636.
Remember statistics come from samples, and parameters come from populations. As long as we were just doing data analysis, searching for patterns or summarizing features of our data, the distinction between population and sample was not as important. Now, as we begin to understand what our data (sample) tell us about a population, it is essential. The notation we use must reflect this distinction. This is why we write p for the proportion in a population and
for the proportion in a sample. The population proportion p is a fixed parameter that is unknown when we use a sample for inference. The sample proportion
is a statistic that would almost certainly take a different value if we chose another sample from the same population.
335
Apply Your Knowledge
Question 15.1
Genetic Engineering. Here’s a new idea for treating advanced melanoma, the most serious kind of skin cancer. Genetically engineer white blood cells to better recognize and destroy cancer cells, then infuse these cells into patients. The subjects in a small initial study of this approach were 11 patients whose melanoma had not responded to existing treatments. One outcome of this experiment was measured by a test for the presence of cells that trigger an immune response in the body and so may help fight cancer. The mean counts of active cells per 100,000 cells for the 11 subjects were 3.8 before infusion and 160.2 after infusion. Is each of the boldface numbers a parameter or a statistic?
Question 15.2
Florida Voters. Florida played a key role in the 2000 and 2004 presidential elections. Voter registration records in October 2012 show that 41% of Florida voters are registered as Democrats and 35% as Republicans. (Most of the others did not choose a party.) To test a random-digit dialing device that you plan to use to poll voters for the next election, you use it to call 250 randomly chosen residential telephones in Florida. Of the registered voters contacted, 34% are registered Democrats. Is each of the boldface numbers a parameter or a statistic?
Question 15.3
Human Growth Hormone. Researchers surveyed 250 American male weight lifters, ranging in age from 18 to 40, to learn about the behaviors of all American male weight lifters in this age range. They found that 12% of them had used human growth hormone (HGH), which has been banned in sports for more than 20 years now. The median usage time for those who reported HGH use was 23 weeks. Is each of the boldface numbers a parameter or a statistic?