15.5 Chapter 15 Summary

Chapter Specifics

• A parameter in a statistical problem is a number that describes a population, such as the population proportion p. To estimate an unknown parameter, use a statistic calculated from a sample, such as the sample proportion .
• The law of large numbers for proportions states that the actual observed sample proportion must approach the population proportion p as the number of observations increases.
• The sampling distribution of a statistic describes the values of the statistic in all possible samples of the same size from the same population.
• When the sample is an SRS from the population, the mean of the sampling distribution of the sample proportion is the same as the population proportion p. That is, is an unbiased estimator of p.
• The standard deviation of the sampling distribution of is 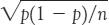for an SRS of size n when the population proportion is p. The standard deviation of the sampling distribution gets smaller only at the rate .
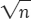• Choose an SRS of size n from a population with population proportion p. When n is large, the sampling distribution of is approximately Normal. We can use the distribution to calculate approximate probabilities for events involving , provided both np and n(1 − p) are 10 or more.

Link It

As we mentioned in Chapter 11, probability is the tool we will use to generalize from data produced by random samples and randomized comparative experiments to some wider population. In this chapter we begin to formalize this process. We use a statistic to estimate an unknown parameter. We use the sampling distribution to summarize the behavior of a statistic in all possible random samples of the same size from a population.

More specifically, in this chapter we begin to think about how a sample proportion, , can provide information about a population proportion, p. When the sample proportion is computed from an SRS drawn from a large population, its sampling distribution has properties that help us understand how the sample proportion can be used to draw conclusions about a population proportion. The law of large numbers tells us that a sample proportion computed from a random sample from some population gets closer and closer to the population proportion as the sample size increases. The approximate Normality of the sampling distribution of the sample proportion for “large” SRSs allows us to make probability statements about possible values of the sample proportion. In the next two chapters, we will develop specific methods for drawing conclusions about a population proportion based on a sample proportion computed from an SRS. These methods will use the tools developed in this chapter.