Appendix 9: Powers-of-Ten Notation
Powers-of-Ten Notation: Large Numbers
Astronomers avoid such confusing terms as “a million billion billion” by using a standard shorthand system called powers-of-ten notation. All the cumbersome zeros that accompany a large number are consolidated into one term consisting of 10 followed by an exponent, which is written as a superscript. The exponent indicates how many zeros you would need to write out the long form of the number. Thus,

and so forth. The exponent also tells you how many tens must be multiplied together to give the desired number, which is why the exponent is also called the power of ten. For example, ten thousand can be written as 104 (“ten to the fourth” or “ten to the fourth power”) because 104 = 10 × 10 × 10 × 10 = 10,000.
In powers-of-ten notation, numbers are written as a figure between one and ten multiplied by the appropriate power of ten. The approximate distance between Earth and the Sun, for example, can be written as 1.5 × 108 kilometers (or 1.5 × 108 km for short). Once you get used to it, this is more convenient than writing “150,000,000 kilometers” or “one hundred and fifty million kilometers.” (The same number could also be written as 15 × 107 or 0.15 × 109, but the preferred form is always to have the first figure be between 1 and 10.)
Calculators and Powers-of-Ten Notation
Most electronic calculators use a shorthand for powers-of-ten notation. To enter the number 1.5 × 108, you first enter 1.5, then press a key labeled “EXP” or “EE,” then enter the exponent 8. (The EXP or EE key takes care of the “× 10” part of the expression.) The number will then appear on your calculator’s display as “1.5 E 8,” “1.5 8,” or some variation of this; typically the “× 10” is not displayed as such. There are some variations from one kind of calculator to another, so you should spend a few minutes reading over your calculator’s instruction manual to make sure you know the correct procedure for working with numbers in powers-of-ten notation. You will be using this notation continually in your study of astronomy, so this is time well spent.
Powers-of-Ten Notation: Small Numbers
You can use powers-of-ten notation for numbers that are less than one by using a minus sign in front of the exponent. A negative exponent tells you to divide by the appropriate number of tens. For example, 10−2 (“ten to the minus two”) means to divide by 10 twice, so 10−2 = 1/10 × 1/10 = 1/100 = 0.01. This same idea tells us how to interpret other negative powers of ten:
A-9

and so forth.
As these examples show, negative exponents tell you how many tenths must be multiplied together to give the desired number. For example, one ten-thousandth, or 0.0001, can be written as 10−4 (“ten to the minus four”) because 10−4 = 1/10 × 1/10 × 1/10 × 1/10 = 0.0001.
A useful shortcut in converting a decimal to powers-of-ten notation is to notice where the decimal point is. For example, the decimal point in 0.0001 is four places to the left of the “1,” so the exponent is −4, that is, 0.0001 = 10−4.
You can also use powers-of-ten notation to express a number like 0.00245, which is not a multiple of 1/10. For example, 0.00245 = 2.45 × 0.001 = 2.45 × 10−3. (Again, the standard for powers-of-ten notation is that the first figure is a number between one and ten.) This notation is particularly useful when dealing with very small numbers. A good example is the diameter of a hydrogen atom, which is much more convenient to state in powers-of-ten notation (1.1 × 10−10 meter, or 1.1 × 10−10 m) than as a decimal (0.00000000011 m) or a fraction (110 trillionths of a meter.)
Because it bypasses all the awkward zeros, powers-of-ten notation is ideal for describing the size of objects as small as atoms or as big as galaxies. Powers-of-ten notation also makes it easy to multiply and divide numbers that are very large or very small.
Arithmetic with Powers-of-Ten Notation
Using powers-of-ten notation makes it easy to multiply numbers. For example, suppose you want to multiply 100 by 1000. If you use ordinary notation, you have to write a lot of zeros:
100 × 1000 = 100,000 (one hundred thousand)
By converting these numbers to powers-of-ten notation, we can write this same multiplication more compactly as
102 × 103 = 105
Because 2 + 3 = 5, we are led to the following general rule for multiplying numbers expressed in terms of powers of ten: Simply add the exponents.
Example: 104 × 103 = 104+3 = 107
To divide numbers expressed in terms of powers of ten, remember that 10−1 = 1/10, 10−2 = 1/100, and so on. The general rule for any exponent n is
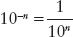
In other words, dividing by 10n is the same as multiplying by 10−n. To carry out a division, you first transform it into multiplication by changing the sign of the exponent, and then carry out the multiplication by adding the exponents. Example:
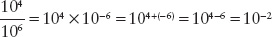
A-10