Answers
ConceptChecks
ConceptCheck 10-1: A very nearby flashlight will appear much brighter than a very distant spotlight. Although a large spotlight emits more light than a small flashlight, which of them appears brighter depends on distance.
ConceptCheck 10-2: The parallax angle is smallest for the most distant stars, so if a parallax angle was measured to be too small, then the astronomer would assume the star is farther away than it actually is.
ConceptCheck 10-3: Parallax only works for stars that are relatively nearby, and the majority of stars in our Galaxy are much too far away to exhibit any apparent shift in position as Earth orbits the Sun.
ConceptCheck 10-4: Because a star’s apparent magnitude when viewed from a distance of 10 pc is the same as its absolute magnitude, both magnitudes would be the same, +4.8.
ConceptCheck 10-5: From Earth, Tau Ceti appears to be relatively bright at +3. However, if it were viewed from a distance of 10 pc, it would appear much dimmer, at +6. The only way this can be is if Tau Ceti is much closer to Earth than 10 pc.
ConceptCheck 10-6: According to the inverse-square law nature of light, the intensity of the light received decreases with the square of the distance. In this instance, increasing the distance 3 times means the newspaper receives only 1/(3)2 or one-ninth the amount of light it originally received.
ConceptCheck 10-7: Because green light has a shorter wavelength than yellow light, the star that is primarily emitting green light must be at a higher temperature than a star emitting mostly yellow light.
ConceptCheck 10-8: The characteristic that most dominates is the prominence of certain hydrogen absorption lines visible in the star, with A class being the greatest and O class being the least.
ConceptCheck 10-9: In the sequence OBAFGKM, F-spectral class stars with designations F1, F2, F3, and F4 are more similar to A-spectral class stars and F6, F7, F8, and F9 are more similar to G-spectral class stars.
ConceptCheck 10-10: No. Within a particular spectral class, the larger numbers correspond to cooler stars. For example, a G2 star is hotter than a G8 star because a G2 is closer to the hotter F-spectral class stars in the sequence OBAFGKM.
ConceptCheck 10-11: In the hottest stars, the electrons have been removed from the hydrogen atoms and, as a result, the existing hydrogen atoms do not have an electron available to create absorption spectra.
ConceptCheck 10-12: Given that the modern spectral sequence of stars and brown dwarfs from hottest to coolest is OBAFGKMLT, L-spectral class brown dwarfs are hotter than T-spectral class brown dwarfs.
ConceptCheck 10-13: Almost all stars and brown dwarfs have similar chemical composition: about three-quarters hydrogen, one-quarter helium, and 1% or less metals.
ConceptCheck 10-14: A bonfire often extends over a large area so that it has an enormously high luminosity, even at the same temperature of a match or a hand lighter.
ConceptCheck 10-15: In low-density atmospheres of the largest stars, atoms tend to be widely separated and have relatively fewer collisions with other atoms that result in light being emitted at highly specific wavelengths that are observed as narrower lines.
ConceptCheck 10-16: If two stars orbiting a common center of mass were moved farther apart, their masses would not change, but the period would increase following Kepler’s third law.
ConceptCheck 10-17: The H-R diagram is plotted as increasing luminosity on the vertical axis and decreasing temperature along the horizontal axis. The stars with the greatest luminosity and the highest temperatures are found in the upper left-hand corner of the H-R diagram.
ConceptCheck 10-18: According to the mass-luminosity relation, the most luminous main-sequence stars are also the most massive, have the largest radii, and have the greatest temperatures.
ConceptCheck 10-19: Main-sequence stars are luminosity class “V,” whereas giant stars are luminosity class “II.” In this instance, the two stars have the same temperature because they are in the same spectral class, but the luminosity class II star is larger and has a greater luminosity than the much smaller main-sequence star.
CalculationChecks
CalculationCheck 10-1: Given that distance in parsecs is the inverse of the parallax angle, d = 1/0.7772, then d = 1.35 pc. Because 1 pc is 3.26 ly, we find that 1.35 pc × (3.26 ly/1 pc) = 4.4 ly.
CalculationCheck 10-2: Pleione’s luminosity to that of the Sun (L/L⊙ = 190) and the ratio of their apparent brightnesses (b/b⊙ = 3.19 × 10−13), when rearranged in the equation relating luminosity, distance, and brightness, yields the distance from Earth to Pleione as 2.44 × 107 times greater than the distance from Earth to the Sun.
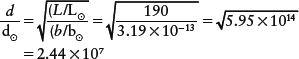
CalculationCheck 10-3: If luminosity is given by the Stefan-Boltzmann law where L = 4πR2σT4, then if radius R is tripled, then L must increase by the R2, which is, in this instance, 32 or 9 times, for a star 3 times larger but at the same temperature.