10-1 Measuring the distances to nearby stars utilizes an effect called parallax

The vast majority of stars visible in the night sky are glowing objects very much like the Sun, only much farther away. But if they appear only as tiny pinpoints of light, even in large telescopes, how can we measure the distances to the stars? You might try to estimate distances by comparing the relative brightnesses of different stars, thinking that all stars emit the same amount of energy, with the more distant ones appearing dimmer. Perhaps the brightly shining star Betelgeuse, in the constellation Orion, appears so bright because it is relatively close, while the dimmer and less conspicuous star Polaris (the North Star, in the constellation Ursa Minor) is farther away.

But this line of reasoning is incorrect: Polaris is actually closer to us than the seemingly brighter Betelgeuse! How bright a star appears is not a good indicator of its distance. If you see a light on a darkened road, it could be a motorcycle headlight a kilometer away or a person holding a flashlight just a few meters away. In the same way, a bright star might be extremely far away but have an unusually high luminosity, and a dim star might be relatively close but have a rather low luminosity. Astronomers must use other techniques to determine the distances to the stars.

Parallax and the Distances to the Stars

Go to Video 10-1

The most straightforward way of measuring stellar distances uses an effect called parallax. This is the apparent displacement of an object because of a change in the observer’s point of view (Figure 10-1). To see how parallax works, hold your arm out straight in front of you. Now look at the hand on your outstretched arm, first with your left eye closed, and then with your right eye closed. When you close one eye and open the other, your hand appears to shift back and forth against the background of more distant objects.

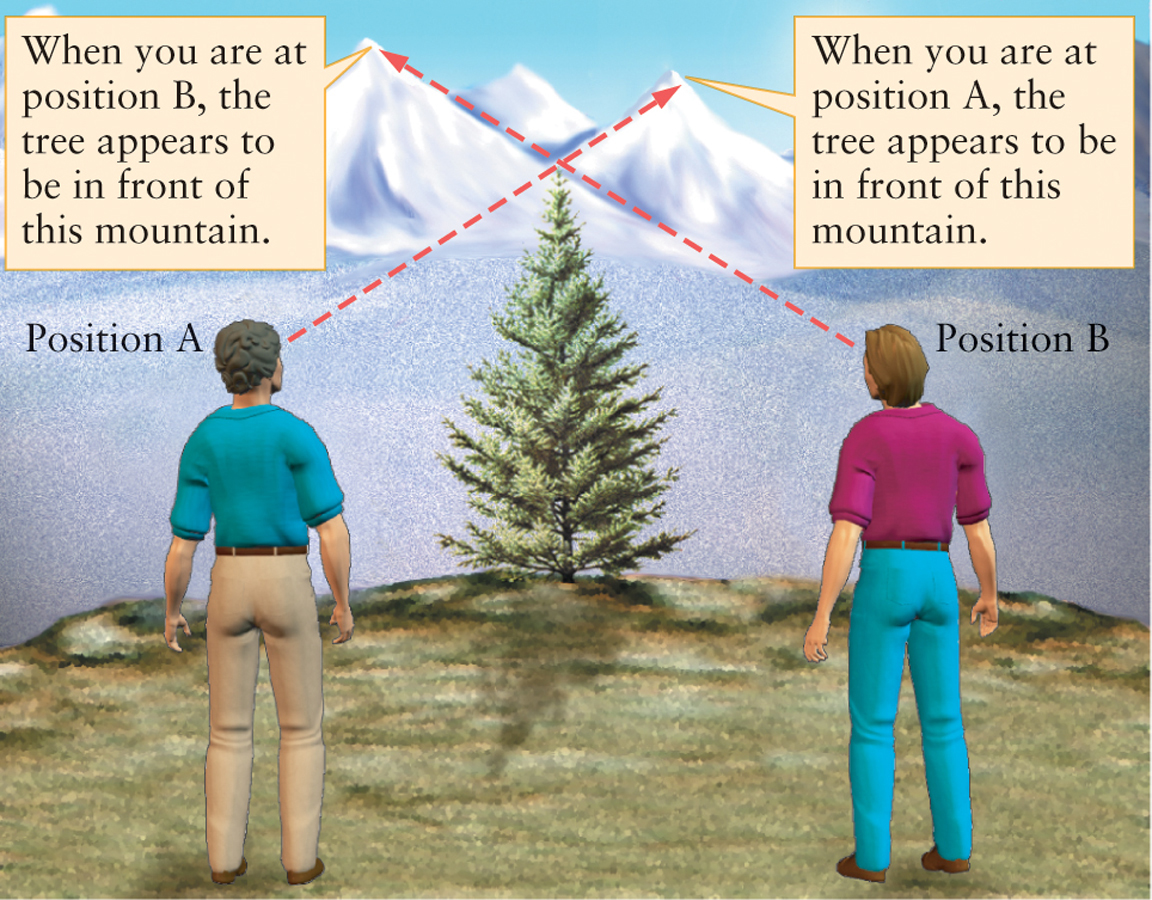
The closer the object you are viewing, the greater the parallax shift. To see this, repeat the experiment with your hand held closer to your face. Your brain analyzes such parallax shifts constantly as it compares the images from your left and right eyes, and in this way determines the distances to objects around you. This is the origin of depth perception.

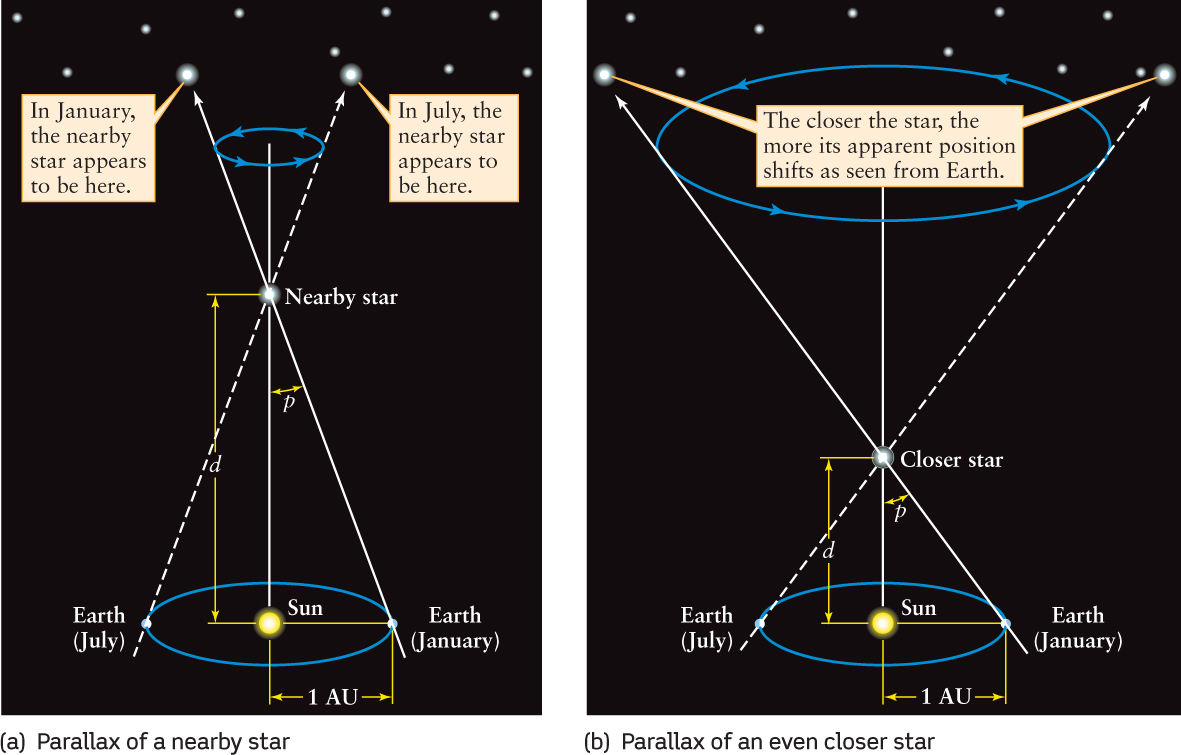
To measure the distance to a star, astronomers measure the parallax shift of the star using two points of view that are as far apart as possible—at opposite sides of Earth’s orbit. The direction from Earth to a nearby star changes as our planet orbits the Sun, and the nearby star appears to move back and forth against the background of more distant stars (Figure 10-2). This motion is called stellar parallax. The parallax (p) of a star is equal to half the angle through which the star’s apparent position shifts as Earth moves from one side of its orbit to the other. The larger the parallax p, the smaller the distance d to the star (compare Figure 10-2a with Figure 10-2b).

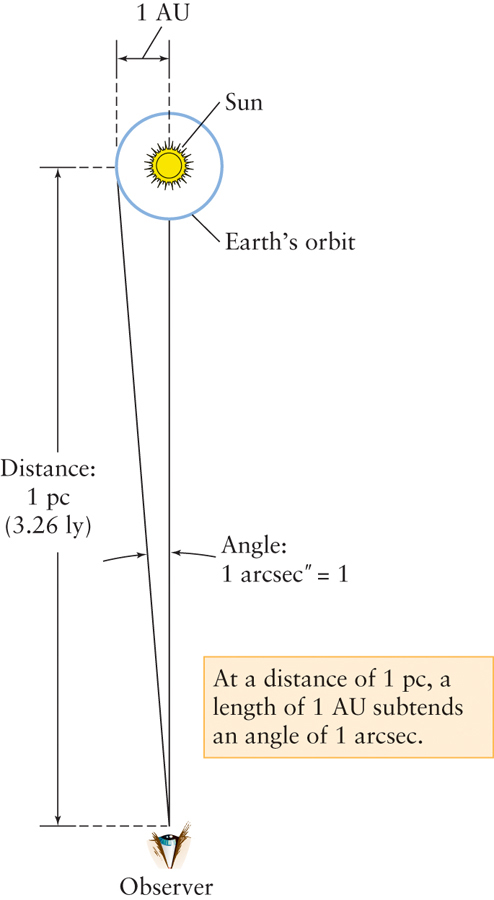
How do we change this apparent shift in position into a distance measurement? Imagine taking a journey far into space, beyond the orbits of the outer planets. As you look back toward the Sun, Earth’s orbit subtends a smaller angle in the sky the farther you are from the Sun. If we use Earth’s distance from the Sun, 1 AU, as our basic measurement, then we can describe distances, d, in parsecs. As Figure 10-3 shows, the distance at which 1 AU stretches across an angle of 1 arcsec is defined as 1 parsec (abbreviated pc). A star with a parallax angle of 1 second of arc (p = 1 arcsec) is at a distance of 1 parsec (d = 1 pc). (The word “parsec” is a contraction of the phrase “the distance at which a star has a parallax of one arcsecond.” One parsec equals 3.26 ly, or 3.09 × 10¹³ km; see Figure 10-3). If the angle p is measured in arcseconds, then the distance d to the star in parsecs is given by the following equation:

Relation between a star’s distance and its parallax

d = distance to a star, in parsecs

p = parallax angle of that star, in arcseconds

This simple relationship between parallax and distance reveals that the closest stars have the greatest parallax. For convenience’s sake, astronomers like to describe distances in parsecs rather than light-years because they use the observed parallax to measure distance.

All known stars have parallax angles less than 1 arcsecond. In other words, the closest star is more than 1 parsec away and, in the same way, the closest star is more than 3.26 light-years away. Such small parallax angles are difficult to detect, so it was not until 1838 that the first successful parallax measurements were made by the German astronomer and mathematician Friedrich Wilhelm Bessel. He found the parallax angle of the star 61 Cygni to be just ⅓ arcsec—equal to the angular diameter of a dime at a distance of 7 mi or 11 km. He thus determined that this star is about 3 pc from Earth. (Modern measurements give a slightly smaller parallax angle, which means that 61 Cygni is actually more than 3 pc away.) Using this strategy, he was able to determine the precise positions of more than 50,000 stars. Today we know that the star Proxima Centauri has the largest known parallax angle, 0.772 arcsec, and hence is the closest known star (other than the Sun)—its distance is 1/(0.772) = 1.30 pc.

Appendix 4 lists all the stars within 4 pc of the Sun, as determined by parallax measurements. These are stars very close to our solar system but still very far beyond the orbits of the planets. Perhaps surprisingly, most of these stars are too dim to be seen with the naked eye, which is why their names are probably unfamiliar to you. In our local neighborhood, most stars are very small and dim.

By stark contrast, the majority of the familiar, named bright stars in the nighttime sky (listed in Appendix 5) are so far away that their parallaxes cannot be measured from Earth’s surface. They appear bright not because they are close, but because they emit far more energy than the Sun. The brightest stars in the sky are not necessarily the nearest stars!

Measuring Parallax from Space

Parallax angles smaller than about 0.01 arcsec are extremely difficult to measure from Earth, in part because of the blurring effects of the atmosphere. Therefore, the parallax method used with ground-based telescopes can give fairly reliable distances only for stars nearer than about 1/0.01 = 100 pc. But an orbiting observatory in space is unhampered by the atmosphere. Observations made from spacecraft therefore permit astronomers to measure even smaller parallax angles and thus determine the distances to more remote stars.

In 1989 the European Space Agency (ESA) launched the satellite Hipparcos, an acronym for High Precision Parallax Collecting Satellite (and a commemoration of the ancient Greek astronomer Hipparchus, who created one of the first star charts). Over more than three years of observations, the telescope aboard Hipparcos was used to measure the parallaxes of 118,000 stars with an accuracy of 0.001 arcsec. This has enabled astronomers to determine stellar distances out to several hundred parsecs, and with much greater precision than has been possible with ground-based observations. In the years to come, astronomers will increasingly turn to space-based observations to determine stellar distances. Unfortunately, most of the stars in the galaxy are so far away that their parallax angles are too small to measure even with an orbiting telescope.

Because it can be used only on relatively close stars, stellar parallax might seem to be of limited usefulness. But parallax measurements are the cornerstone for all other methods of finding the distances to more remote objects. Other methods, which we will get to in later chapters as we look beyond the Milky Way Galaxy, require a precise and accurate knowledge of the distances to nearby stars, as determined by stellar parallax. Hence, any inaccuracies in the parallax angles for nearby stars can translate into substantial errors in measurement for the whole universe. For this reason, astronomers are continually trying to perfect their parallax-measuring techniques.

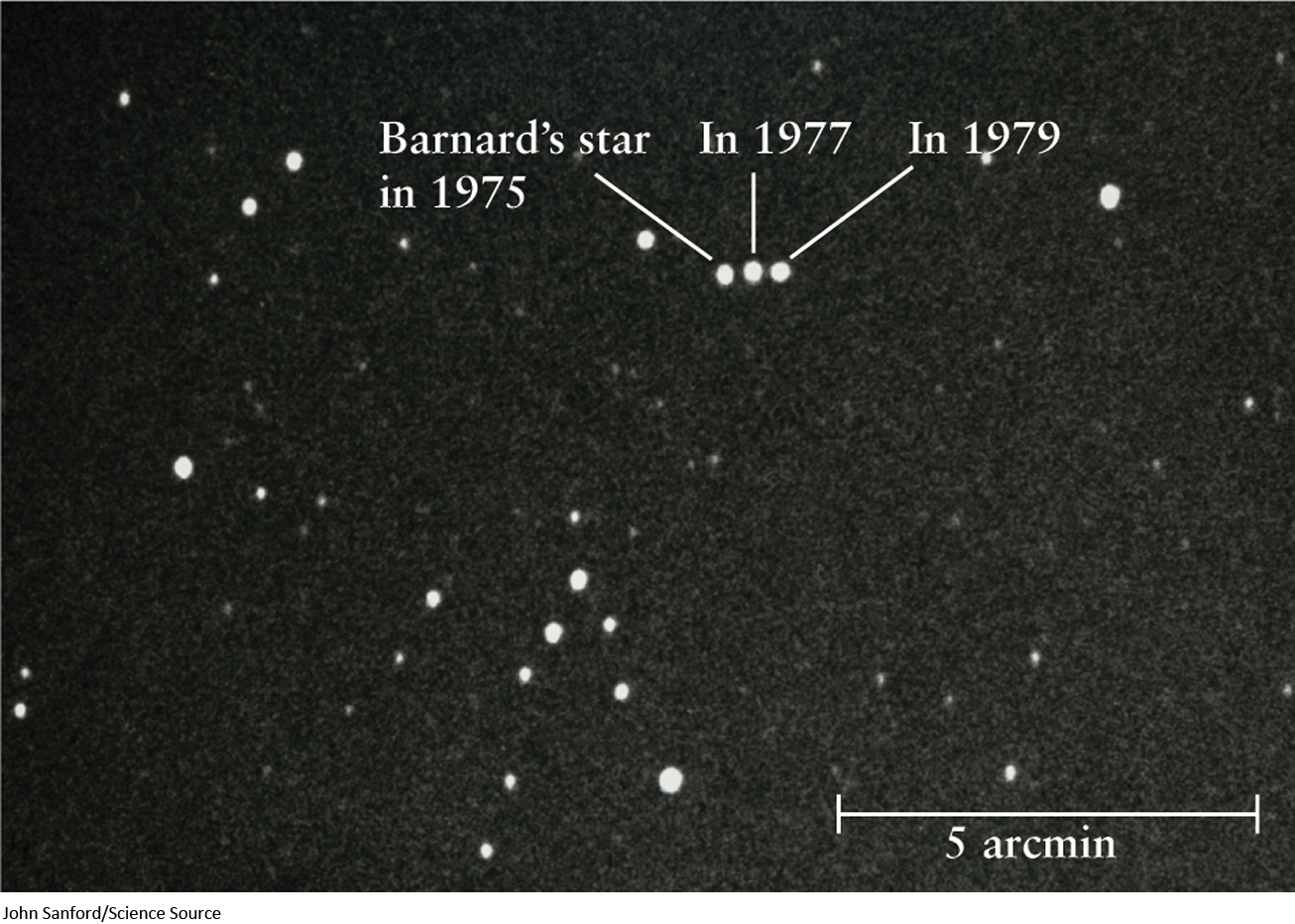
Stellar parallax is an apparent motion of stars caused by Earth’s orbital motion around the Sun. But stars are not fixed objects and actually do move through space. As a result, stars change their positions on the celestial sphere (Figure 10-4). These motions are sufficiently slow, however, that changes in the positions of the stars are hardly noticeable over a human lifetime.