10-6 Stars come in a wide variety of sizes and masses
 Go to Video 10-4
Go to Video 10-4
With even the best telescopes, most stars appear as little more than tiny points of light. On a photograph or CCD image, brighter stars appear larger than dim ones (see Figures 10-5b and 10-11), but these apparent sizes are due to brightness and give no indication of the star’s actual size. So, how could you determine the diameter of an object that is so distant it has no apparent size? One strategy is to combine information about a star’s luminosity (determined from its distance and apparent brightness) and its surface temperature (determined from its spectral type).
Calculating the Radii of Stars
The key to finding a star’s radius from its luminosity and surface temperature is the Stefan-Boltzmann law. This rule shows up again and again in astronomy and simply says that the amount of energy radiated per second from a square meter of a blackbody’s surface—that is, the energy flux (F)—is proportional to the fourth power of the temperature of that surface (T), as given by the equation F = σT4. In other words, how much light a star emits is highly dependent on its temperature, with the hottest stars emitting significantly more energy than cooler stars. (Absorption lines, while important for determining the star’s chemical composition and surface temperature, make only relatively small modifications to a star’s spectrum.)
A star’s luminosity is the amount of energy emitted per second from its entire surface. This equals the energy flux F multiplied by the total number of square meters on the star’s surface (that is, the star’s surface area). We expect that most stars are nearly spherical, like the Sun, so we can use the formula for the surface area of a sphere. This is 4πR2, where R is the star’s radius (the distance from its center to its surface). Multiplying together the formulas for energy flux and surface area to make a powerful mathematical relationship that can be easily applied, we can write the star’s luminosity as follows:
Relationship between a star’s luminosity, radius, and surface temperature
L = 4πR2σT4
L = star’s luminosity, in watts
R = star’s radius, in meters
σ = Stefan-Boltzmann constant = 5.67 × 10−8 W m−2 K−4
T = star’s surface temperature, in degrees Kelvin
This equation might look complicated, but it simply says that a relatively cool star (low surface temperature T), for which the energy flux is quite low, can nonetheless be very luminous if it has a large enough radius R. Alternatively, a relatively hot star (large T) can have a very low luminosity if the star has only a little surface area (small R). Box 10-1 Tools of the Astronomer’s Trade: Stellar Radii, Luminosities, and Surface Temperatures describes and provides examples on how to use the above equation to calculate a star’s radius if its luminosity and surface temperature are known.
ANALOGY
In a similar way, a roaring campfire can emit more light than a welder’s torch. The campfire is at a lower temperature than the torch but has a much larger surface area from which it emits light.
Question
ConceptCheck 10-14: What makes lighting a candle using a large, roaring bonfire much more difficult than using a hand lighter of the same temperature?
Question
CalculationCheck 10-3: If two stars are at the same temperature, but one is 3 times larger, how many times more luminous is it?
239
TOOLS OF THE ASTRONOMER’S TRADE
Stellar Radii, Luminosities, and Surface Temperatures
Because stars emit light in almost exactly the same fashion as blackbodies, we can use the Stefan-Boltzmann law to relate a star’s luminosity (L), surface temperature (T), and radius (R). The relevant equation is
L = 4πR2σT4
As written, this equation involves the Stefan-Boltzmann constant r, which is equal to 5.67 × 10−8 W m−2 K−4. In many calculations, it is more convenient to relate everything to the Sun, which is a typical star. Specifically, for the Sun we have 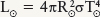 , where L⊙ is the Sun’s luminosity, R⊙ is the Sun’s radius, and T⊙ is the Sun’s surface temperature (equal to 5800 K). Dividing the general equation for L by this specific equation for the Sun, we obtain
, where L⊙ is the Sun’s luminosity, R⊙ is the Sun’s radius, and T⊙ is the Sun’s surface temperature (equal to 5800 K). Dividing the general equation for L by this specific equation for the Sun, we obtain
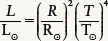
This is an easier formula to use because the constant r has cancelled out. We can also rearrange terms to arrive at a useful equation for the radius (R) of a star:
Radius of a star related to its luminosity and surface temperature
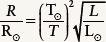

EXAMPLE: The bright reddish star Betelgeuse in the constellation Orion (see Figure 10-5a) is 60,000 times more luminous than the Sun and has a surface temperature of 3500 K. What is its radius?
Situation: We are given the star’s luminosity L = 60,000 L⊙ and its surface temperature T = 3500 K. Our goal is to find the star’s radius R.
Tools: We use the equation for the radius of a star to find the ratio of the star’s radius to the radius of the Sun, R/R⊙. Note that we also know the Sun’s surface temperature, T⊙ 5800 K.
Answer: Substituting these data into the equation, we get

Review: Our result tells us that Betelgeuse’s radius is 670 times larger than that of the Sun. The Sun’s radius is 6.96 × 105 km, so we can also express the radius of Betelgeuse as (670)(6.96 × 105 km) = 4.7 × 108 km. This is more than 3 AU. If Betelgeuse were located at the center of our solar system, it would extend beyond the orbit of Mars!
EXAMPLE: Sirius, the brightest star in the sky, is actually two stars orbiting each other (a binary star). The less luminous star, Sirius B, is a white dwarf that is too dim to see with the naked eye. Its luminosity is 0.0025 L⊙ and its surface temperature is 10,000 K. How large is Sirius B compared to Earth?
Situation: Again we are asked to find a star’s radius from its luminosity and surface temperature so we can compare it to Earth’s size.
Tools: We use the same equation as in the preceding example.
Answer: The ratio of the radius of Sirius B to the Sun’s radius is
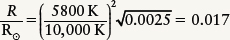
Since the Sun’s radius is R⊙ = 6.96 × 105 km, the radius of Sirius B is (0.017)(6.96 × 105 km) = 12,000 km. Because Earth’s radius (half its diameter) is 6378 km, this star is only about twice the radius of Earth.
Review: Although Sirius B’s radius is large compared to a terrestrial planet, it is a minuscule size for a star. The name dwarf is well deserved!
Determining a Star’s Size from its Spectrum
You might wonder if the details of a star’s size can be deduced from characteristics of its absorption spectrum, and in fact they can be. Figure 10-12 compares the spectra of two stars of the same spectral type and temperature but different luminosity (and hence different size): a B8 supergiant star and a more common B8 star. Note that the most prominent lines of hydrogen are narrow in the spectrum of the very large, very luminous supergiant but quite broad in the spectrum of the small, less luminous star. In general, for stars of spectral types B through F, the larger and more luminous the star, the narrower is its hydrogen line.

Fundamentally, these differences between stars of different luminosity are due to differences between the stars’ atmospheres, where absorption lines are produced. Hydrogen lines in particular are affected by the density and pressure of the gas in a star’s atmosphere. The higher the density and pressure, the more frequently hydrogen atoms collide and interact with other atoms and ions in the atmosphere. These collisions shift the energy levels in the hydrogen atoms and thus broaden the hydrogen spectral lines.
240
Astronomers find that stars come in a wide range of sizes. The smallest stars visible through ordinary telescopes, called white dwarfs, are about the same size as Earth. Although their surface temperatures can be very high (25,000 K or more), white dwarfs have so little surface area that their luminosities are very low (less than 0.01 L⊙). The largest stars, called supergiants, are a thousand times larger in radius than the Sun and 105 times larger than white dwarfs. If our own Sun were replaced by one of these supergiants, Earth’s orbit would lie completely inside the star! (White dwarfs and supergiants are covered in more detail in Section 10-7.)
In the atmosphere of a luminous giant star, the density and pressure are quite low because the star’s mass is spread over a huge volume. Atoms and ions in the atmosphere are relatively far apart; hence, collisions between them are sufficiently infrequent that hydrogen atoms can produce narrower lines. A smaller star, however, is much more compact than a giant or supergiant. In the denser atmosphere of a typical, Sunlike star, frequent interatomic collisions perturb the energy levels in the hydrogen atoms, thereby producing broader lines.
Question
ConceptCheck 10-15: What about the nature of atoms in Sunlike stars makes the notion that the “larger stars have the broadest absorption lines” incorrect?
Observing Binary Star Systems Reveals the Masses of Stars
We now know something about the sizes, temperatures, and luminosities of stars and how one aspect influences the others. To complete our picture of the physical properties of stars, we need to know how much material these stars are made of—their masses. In this section, we will see that stars come in a wide range of masses. We will also discover an important relationship between the mass and luminosity of unique stars. This relationship is crucial to understanding why some stars are hot and luminous, while others are cool and dim. It will also help us understand what happens to a star as it ages and evolves.
Determining the masses of stars is not an easy task by any means. The problem is that there is no practical, direct way to measure the mass of an isolated star. Fortunately for astronomers, about half of the visible stars in the night sky are not isolated individuals. Instead, they are multiple-star systems, in which two or more stars orbit each other. By carefully observing the motions of these stars, astronomers can glean important information about their masses.
A pair of stars located at nearly the same position in the night sky is called a double star. The German-born British astronomer William Herschel—who discovered Uranus—made the first organized search for such pairs. Between 1782 and 1821, he published three catalogs listing more than 800 double stars. Late in the nineteenth century, his son, John Herschel, discovered 10,000 more doubles. Some of these double stars are two stars that lie along nearly the same line of sight but are actually at very different distances from us. But many double stars are true binary stars, or binaries—pairs of stars that actually orbit each other. Figure 10-13 shows an example of this orbital motion. By observing the binary over an extended period, astronomers can plot the orbit that one star appears to describe around the other, as shown in the center diagram in Figure 10-13.

In fact, both stars in a binary system are in motion. They orbit each other because of their mutual gravitational attraction, and their orbital motions can be calculated by adapting Kepler’s third law for planet orbits to multiple star systems, as follows:
Kepler’s third law for binary star systems
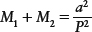

Here a is the semimajor axis of the elliptical orbit that one star appears to describe around the other, plotted as in the center diagram in Figure 10-13. As this equation indicates, if we can measure this semimajor axis (a) and the orbital period (P), we can learn something about the masses of the two stars.
241
In principle, the orbital period of a visual binary is easy to determine. All you have to do is see how long it takes for the two stars to revolve once about each other. The two stars shown in Figure 10-13 are relatively close, about 2.5 AU on average, and their orbital period is only 10 years. Many binary systems have much larger separations, however, and the period may be so long that more than one astronomer’s lifetime is needed to complete the observations.
Each of the two stars in a binary system actually moves in an elliptical orbit about the center of mass of the system. Imagine two children sitting on opposite ends of a playground seesaw (Figure 10-14a). For the seesaw to balance properly, they must position themselves so that their center of mass—an imaginary point that lies along a line connecting their two bodies—is at the pivot point of the seesaw. If the two children have the same mass, the center of mass lies midway between them, and they should sit equal distances from the center. If their masses are different, the center of mass is closer to the heavier child and the children need to readjust their positions in order to easily balance.
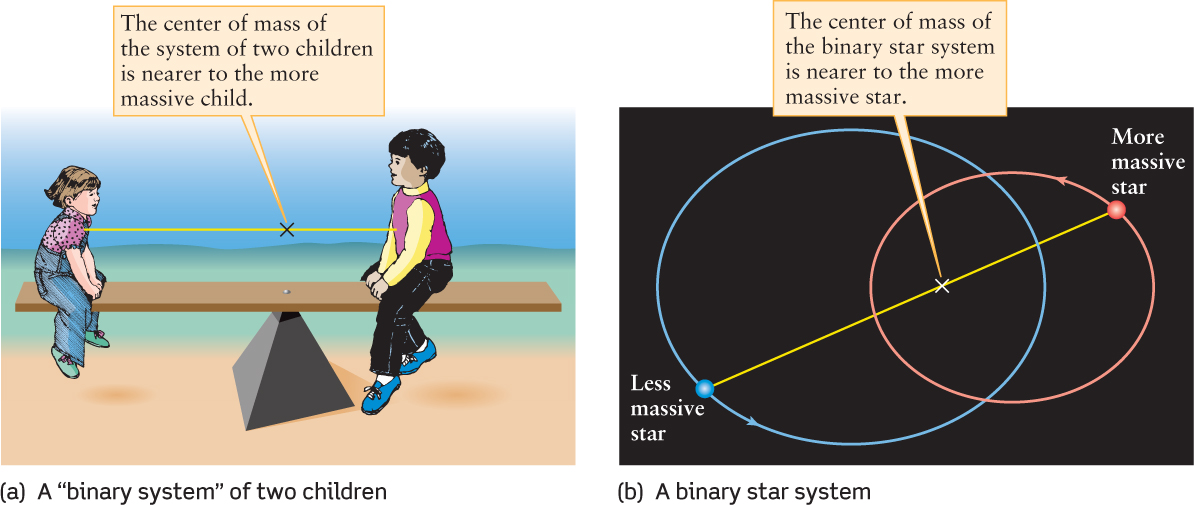
Just as the seesaw naturally balances at its center of mass, the two stars that make up a binary system naturally orbit around their center of mass (Figure 10-14b). The center of mass always lies along the line connecting the two stars and is closer to the more massive star.
The center of mass of a visual binary is located by plotting the separate orbits of the two stars, as in Figure 10-14b. The center of mass lies at the common focus of the two elliptical orbits. Comparing the relative sizes of the two orbits around the center of mass yields the ratio of the two stars’ masses, M1/M2. The sum M1 + M2 is already known from Kepler’s third law, so the individual masses of the two stars can then be determined.
242
Question
ConceptCheck 10-16: If two stars in a binary system were moved farther apart, how would their masses and orbital periods change?