14-8 Supermassive black holes may be the “central engines” that power active galaxies
In 1968, the British astronomer Donald Lynden-Bell pointed out that a black hole lurking at the center of a galaxy could be the “central engine” powering an active galactic nucleus. Lynden-Bell theorized that as gases fall onto a black hole, their gravitational energy would be converted into radiation. To produce as much radiation as is seen from active galactic nuclei, the black hole would have to be very massive indeed.
The Eddington Limit and Black Hole Sizes
How large a black hole would be needed to power an active galactic nucleus? You might think that what really matters is not the size of the black hole, but rather the amount of gas that falls onto it and releases energy. However, there is a natural limit to the luminosity that can be radiated by accretion onto a compact object like a black hole. This is called the Eddington limit, after the British astrophysicist Sir Arthur Eddington.
If the luminosity exceeds the Eddington limit, there is so much radiation pressure—the pressure produced by photons streaming outward from the infalling material—that the surrounding gas is pushed away rather than falling inward onto the black hole. Without a source of gas to provide energy, the luminosity naturally decreases to below the Eddington limit, at which point gas can again fall inward. This limit allows us to calculate the minimum mass of an active galactic nucleus.
Numerically, the Eddington limit is:
The Eddington limit
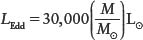
LEdd = maximum luminosity that can be radiated by accretion onto a compact object
M = mass of the compact object
M⊙ = mass of the Sun
L⊙ = luminosity of the Sun
What this means is that the mass of the black hole must also be quite large because the tremendous luminosity of an active galactic nucleus must be less than or equal to its Eddington limit.
Astronomers have indeed found evidence for such supermassive black holes at the centers of many nearby normal galaxies. As we saw in section 13-6, at the center of our own Milky Way Galaxy lies what is almost certainly a black hole of about 3.7 × 106 solar masses—supermassive in comparison to a star, but less than 1% the mass of the behemoth black hole at the center of 3C 273.
Theory suggests that unlike stellar-mass black holes, which require a supernova to produce them, supermassive black holes can be produced without extreme pressures or densities. This may help to explain why they appear to be a feature of so many galaxies.
Question
ConceptCheck 14-17: What keeps a supermassive black hole from having an unlimited luminosity?
Question
CalculationCheck 14-2: If one supermassive black hole has twice the mass of a second supermassive black hole, how is its Eddington limit different?
Measuring Black Hole Masses in Galaxies
One galaxy that probably has a black hole at its center is the Andromeda Galaxy (M31), shown in Figure 14-2. M31 is only 2.5 million ly from Earth, close enough that details in its core as small as 3 ly across can be resolved under the best seeing conditions.
In the mid-1980s, astronomers made high-resolution spectroscopic observations of M31’s core. By measuring the Doppler shifts of spectral lines at various locations in the core, we can determine the orbital speeds of the stars about the galaxy’s nucleus.
Figure 14-33 plots the results for the innermost 1000 ly of M31. Note that the rotation curve in the galaxy’s nucleus does not follow the trend set in the outer core. Rather, there are sharp peaks—one on the approaching side of the galaxy and the other on the receding side—within 5 arcsec of the galaxy’s center.

351
The most straightforward interpretation is that the peaks are caused by the orbital motions of stars around M31’s center. Stars on one side of the galaxy’s center are approaching us while stars on the other side are receding from us.
The high speeds of stars orbiting close to M31’s center indicate the presence of a massive central object. We can use Newton’s form of Kepler’s third law and our knowledge of these stars’ orbital speeds to calculate the mass of this object. Similarly, this is the same method we use to calculate the mass of the supermassive black hole at the center of our Milky Way Galaxy. The difference is that we can track individual stars at the center of our Galaxy, while the data in Figure 14-33 come from the combined light of many stars in M31. Such calculations show that there must be about 3 × 107 solar masses within 16 ly of the center of M31. That much matter confined to such a small volume strongly suggests the presence of a supermassive black hole. Observations of M31 with the Chandra X-ray Observatory are consistent with this picture.
By applying high-resolution spectroscopy to the cores of other nearby galaxies, astronomers have discovered a number of supermassive black holes like the one in M31. Unfortunately, this technique for identifying black holes is difficult to apply to quasars, which are very distant and have small angular sizes. The evidence for supermassive black holes in quasars is therefore circumstantial, yet compelling: No other known energy source could provide enough power to sustain a quasar’s intense light output.
Question
ConceptCheck 14-18: How is the evidence for supermassive black holes in nearby galaxies different from the evidence for supermassive black holes in distant quasars?