2-2 Glowing objects, like stars, emit an entire spectrum of light
Many people who have felt the warmth of the sunshine on a clear summer’s day have wondered, “What is light?” We know that it has energy because light “feels” warm when it comes from the Sun. What else can we learn about light by studying it? As early as the 1600s, scientists started to reveal the important characteristics of light: that it is a mixture of all the colors of the rainbow; that it travels in waves and has electric and magnetic properties; and that light visible to the human eye is only one small part of the entire spectrum of light.
Sunlight is a Mixture of All Colors
What color is sunlight? Observing the dusk at sunset might persuade you to believe that sunlight is reddish-pink. A quick (but potentially very harmful!) glance at the Sun through thin clouds might lead you to change your mind to believe that sunlight is actually white. If you hold a piece of white paper in a beam of sunlight, the paper appears to be bright white. Alternatively, if you hold a piece of blue paper in that same beam of sunlight, the paper appears bright blue. The same observation holds true with red paper, green paper, and yellow paper. In the end, capturing a ray of sunlight to determine its color is tricky indeed.
Another experimental approach to studying the nature of light is to observe what happens when light is separated into a rainbow of colors, when it reflects off an evenly scratched surface, such as a DVD. The same thing can happen when light passes through a raindrop, causing a rainbow of colors in the sky. However, we can study light more precisely when it passes through carefully designed materials, such as a glass prism (Figure 2-2). The first recorded experiment on passing light through a glass prism was performed by Isaac Newton around 1670. Newton was familiar with what he called the “celebrated Phenomenon of Colours,” in which a beam of sunlight passing through a glass prism spreads out into the colors of the rainbow. This rainbow of all colors is called a spectrum (plural spectra).

Until Newton’s time, it was thought that a prism somehow added colors to white light. To test this idea, Newton placed a second prism so that just one color of the spectrum passed through it (Figure 2-3). According to the old thinking, this should have caused a further change in the color of the light. But Newton found that each color of the spectrum was unchanged by the second prism; red remained red, blue remained blue, and so on. These observations led him to conclude that a prism merely separates colors and does not add color. Hence, the spectrum produced by the first prism demonstrates that sunlight is a mixture of all the colors of the rainbow.

36
Question
ConceptCheck 2-2: If you cover a white light with a specially designed green plastic gel so that only the green light passes through, which color plastic cover gel do you need to add to the pure green light to make it change to red?
Light Travels in Waves and Is Also Called Electromagnetic Radiation
Newton suggested that light is composed of particles too small to detect individually. In 1678, the Dutch physicist and astronomer Christiaan Huygens proposed a rival explanation. He suggested that light travels in the form of waves rather than as tiny particles. These two ideas are very different notions about the nature of light. So which is it?
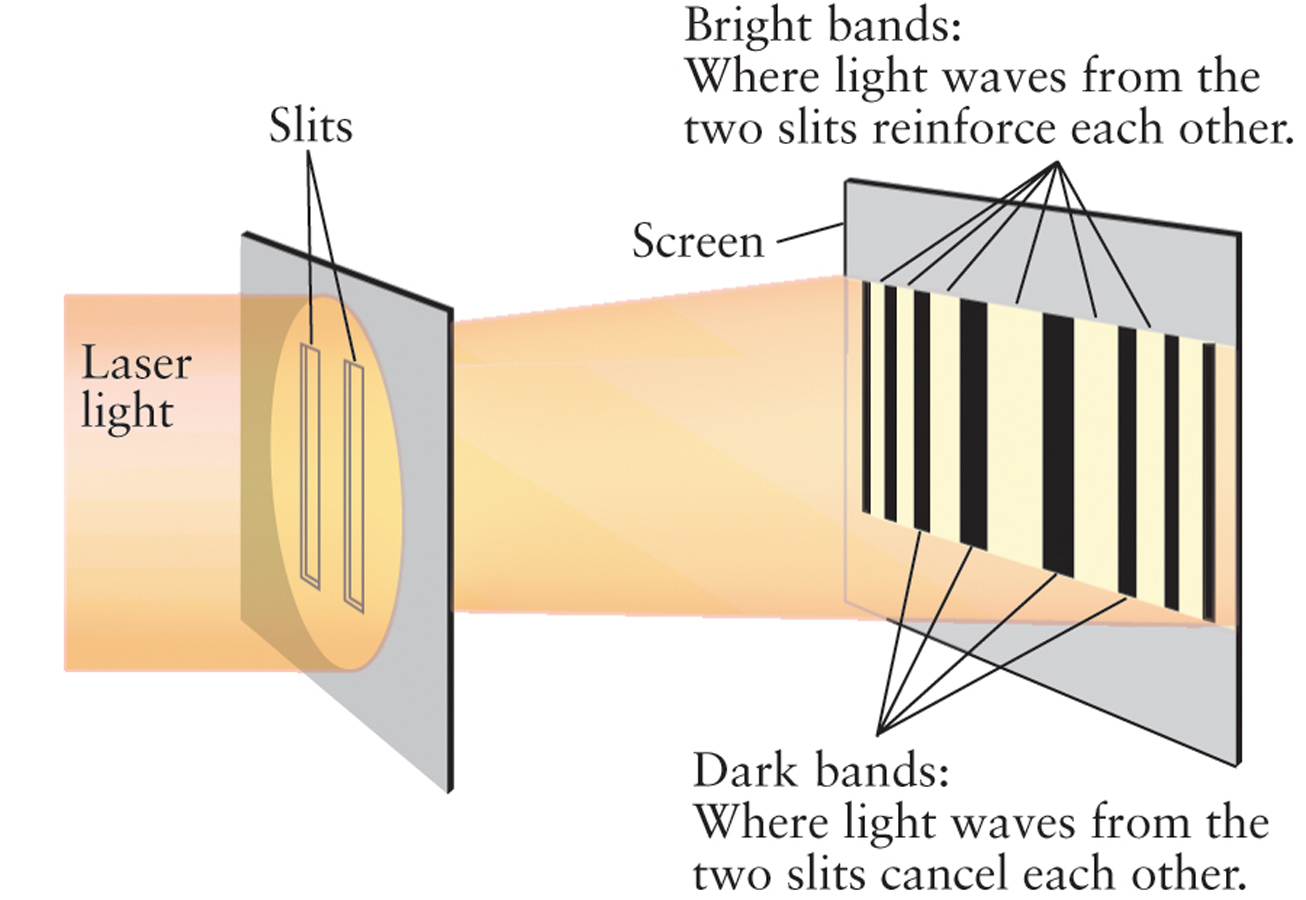
Around 1801, Thomas Young in England carried out an experiment that convincingly demonstrated the wavelike aspect of light. He passed a beam of light through two thin, parallel slits in an opaque screen, as shown in Figure 2-4. On a white surface some distance beyond the slits, the light formed a pattern of alternating bright and dark bands. Young reasoned that if a beam of light was a stream of particles (as Newton had suggested), the two beams of light from the slits should simply form bright images of the slits on the white surface. The pattern of bright and dark bands he observed is just what would be expected, however, if light had wavelike properties. An analogy with water waves demonstrates why.
ANALOGY
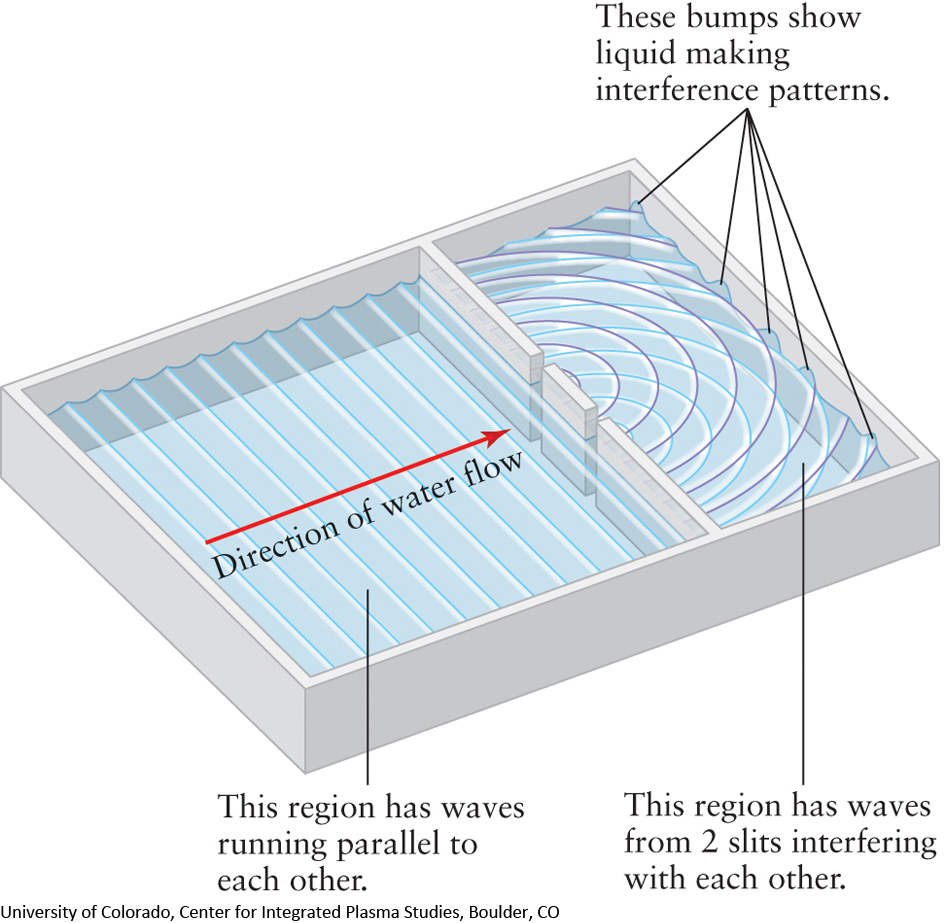
Imagine ocean waves pounding against a reef or breakwater that has two openings (Figure 2-5). A pattern of ripples is formed on the other side of the barrier as the waves come through the two openings and interfere with each other.
At certain points, wave crests arrive simultaneously from the two openings. These reinforce each other and produce high waves. At other points, a crest from one opening meets a trough from the other opening. These cancel each other out, leaving areas of still water. This process of combining two waves also takes place in Young’s double-slit experiment: The bright bands are regions where waves from the two slits reinforce each other, while the dark bands appear where waves from the two slits cancel each other.
This demonstration of the wave nature of light poses some obvious questions. What exactly is “waving” in light? That is, what is it about light that goes up and down like water waves on the ocean? Because we can see light from the Sun, planets, and stars, light waves must be able to travel across empty space. Hence, whatever is “waving” cannot be any material substance. What, then, is it?
The answer is that light is energy. It is a particular kind of energy called electromagnetic energy that can radiate throughout the empty vacuum of outer space. It is a unique kind of energy because some kinds of energy require a material substance to travel through—water waves, for example, can only travel through water. Because of its ability to move by the process of radiation, light is sometimes given the long and somewhat clumsy name of electromagnetic radiation.
CAUTION
You may associate the term radiation with radioactive materials like uranium, but this term refers to anything that radiates, or spreads away, from its source. For example, scientists sometimes refer to sound waves as “acoustic radiation.” Radiation does not have to be related to radioactivity! Although some scientists make a distinction between light and electromagnetic radiation, for our purposes in this book, we use the two interchangeably.
37
Thinking of light as a wave of energy traveling through outer space allows us to describe light in of the same terms as we describe waves, like those shown in Figure 2-5. In addition to energy, we can also describe the distance between two successive wave crests as the wavelength of the light, usually designated by the Greek letter λ (lambda). No matter what the size of the wavelength or the amount of energy in a light wave, light always travels at the same speed c = 300,000 km/s through empty space.
Question
ConceptCheck 2-3: If bigger and more water waves are generated more quickly by tapping the pan in Figure 2-5 more intensely and faster, what happens to the speed that the waves travel through the water?
 Go to Video 2-1
Go to Video 2-1
Our Eyes See Only Some of the Entire Spectrum of Light The human eye is sensitive to only a very narrow range of wavelengths of light. Once scientists determined that there are no size restrictions on the possible wavelengths of light, they realized that light could and should exist with wavelengths both longer and shorter than the range of visible light seen across the entire spectrum of colors in a rainbow. Consequently, they began to look for invisible forms of light—forms of light to which the cells of the retina in a human eye do not respond. As it turns out, when one uses carefully designed sensors, light appears throughout our universe in a much wider variety of wavelengths than were ever imagined to exist.
One of the first kinds of invisible light was discovered around 1800 by the German-born British astronomer and acclaimed musician, Sir William Herschel. Trying to better understand the constituents of sunlight, he passed a beam of sunlight through a prism and held a thermometer just beyond the red end of the visible spectrum. The thermometer registered a temperature increase, indicating that it was being exposed to an invisible form of energy. It was only later that this invisible energy, now called infrared light (IR), was realized to be light with wavelengths somewhat longer than those of visible light.
In 1888, the German physicist Heinrich Hertz succeeded in identifying light with even longer wavelengths than infrared, having wavelengths of several centimeters, now known as radio waves, in experiments with electric sparks. At about the same time and studying light with much shorter wavelengths than visible light, another German physicist, Wilhelm Röntgen, invented a machine that created invisible light with incredibly small wavelengths, now known as X-rays. The X-ray machines in modern medical and dental offices are direct descendants of Röntgen’s invention. Over the years, an entire spectrum of different wavelengths of light has been discovered.
An entire spectrum of light is emitted by glowing objects across the universe, much of which is invisible to human eyes and requires special telescopes to observe.
The surprisingly narrow range of wavelengths of light our human eyes can see, called visible light, occupies only a tiny fraction of the full range of possible wavelengths, collectively called the electromagnetic spectrum (Figure 2-6). To express such tiny distances conveniently, scientists use a unit of length called the nanometer (abbreviated nm), where 1 nm is written as 10−9 m, which means there are nine digits to the right of the decimal place—a very small number indeed.1 Some astronomers prefer to measure wavelengths in angstroms. One angstrom, abbreviated Å, is one-tenth of a nanometer: 1 Ă = 0.1 nm or 10−10 m. Visible light has wavelengths covering the range from about 400 nm for violet light to about 700 nm for red light. Intermediate colors of the rainbow like yellow (550 nm) have intermediate wavelengths. In these units, the wavelengths of visible light shown in Figure 2-6 would extend from about 4,000 Å to about 7,000 Å, instead of 400 nm to 700 nm.

38
Gamma rays are the light waves that have the shortest wavelength. Only a little longer are X-rays, which have wavelengths between about 10 nm and 0.01 nm. At wavelengths just short of visible light, ultraviolet light (UV) extends from about 100 nm down to 10 nm.
For wavelengths of light longer than visible light, infrared light covers the range from about 700 nm to 1 mm. Astronomers interested in infrared light often express wavelength in micrometers or microns, abbreviated μm, where 1 μm = 10−3 mm = 10−6 m. Microwaves have wavelengths from roughly 1 mm to 10 cm, while radio waves have the longest wavelengths.
Question
ConceptCheck 2-4: Which form of light has a wavelength similar to the diameter of your finger?
Frequency Relates to the Number of Wave Crests Passing by Each Second
Although wavelength is a common way to distinguish among the entire spectrum of light emitted by objects, light can also be described in terms of frequency. This is commonly done by astronomers working with radio telescopes who look at the largest wavelengths of light. The frequency (f) of a wave is the number of wave crests that pass a given point in 1 s. Equivalently, it is the number of complete cycles of the wave that pass per second (a complete cycle is from one crest to the next). The unit of frequency is the cycle per second, also called the hertz (abbreviated Hz) in honor of Heinrich Hertz, the physicist who first produced radio waves. For example, if 500 crests of a wave pass you in 1 second, the frequency of the wave is 500 cycles per second or 500 Hz.
In working with frequencies, it is often convenient to use the prefix mega- (meaning “million,” or 106, and abbreviated M) or kilo- (meaning “thousand,” or 103, and abbreviated k). For example, AM radio stations broadcast at frequencies between 535 kHz and 1605 kHz (kilohertz), while FM radio stations broadcast at frequencies in the range from 88 MHz to 108 MHz (megahertz).
The relationship between the frequency and wavelength of an electromagnetic wave is relatively straightforward. Because light in a vacuum moves at a constant speed c = 300,000 km/s, if the wavelength—distance from one crest to the next—is made shorter, then the frequency must increase because more of those closely spaced crests pass by you each second.
The frequency f of light is inversely related to its wavelength λ, such that when one value is large, the other value is small. This idea can also be expressed as a simple equation as
Frequency and wavelength of an electromagnetic wave
f = c/λ
f = frequency of an electromagnetic wave (in hertz)
c = speed of light (in meters/second) = 300,000,000 m/s
λ = wavelength of the wave (in meters)
That is, the frequency of a wave equals the wave speed divided by the wavelength. What this relationship means is that the longest wavelengths of light have the lowest frequencies.
For example, hydrogen atoms in space emit radio waves with a wavelength of 21.12 cm. To calculate the frequency of this electromagnetic wave using the equation c = f × λ, we must first express the wavelength in meters rather than centimeters: λ = 0.2112 m. Then we can use the above formula to find the frequency f:
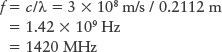
Visible light has a much shorter wavelength and higher frequency than radio waves. You can use the above formula to show that for yellow-orange light of wavelength 600 nm, the frequency is 5 × 1014 Hz or, with this many zeros, 500 million MHz!
Question
ConceptCheck 2-5: How do the frequencies of the longest wavelengths of light compare to the frequencies of the shortest wavelengths of light?
Question
CalculationCheck 2-1: What is the wavelength of radio waves from a nearby FM radio station?