2-5 An object’s motion through space is revealed by the precise wavelength positions of its spectrum of light
Often, astronomical reports in the media describe the speed at which astronomical objects are moving. Or, Hollywood takes a turn at illustrating science, and impending doom is imminent because of the asteroid or meteor speeding our way. How might one go about determining the speed of a star moving through space? If the star is moving side to side, one could reasonably hope to simply measure how far it moves in a particular amount of time. But, what if the object is moving toward us or away from us? Fortunately, in addition to telling us about temperature and chemical composition, the spectrum of a planet, star, or galaxy can also reveal something about that object’s motion through space.
Exploiting the Doppler Effect
 Go to Video 2-3
Go to Video 2-3
In 1842, Christian Doppler, a professor of mathematics in Prague, pointed out that the observed wavelength of light must be affected by motion. Figure 2-17 shows why. In this figure, a light source is moving from right to left, and the circles represent the crests of waves emitted from the moving source at various positions. Each successive wave crest is emitted from a position slightly closer to the observer on the left, so she sees a shorter wavelength—the distance from one crest to the next—than she would if the source were stationary. All the lines in the spectrum of an approaching source are shifted toward the short-wavelength (blue) end of the spectrum. This phenomenon is called a blueshift.
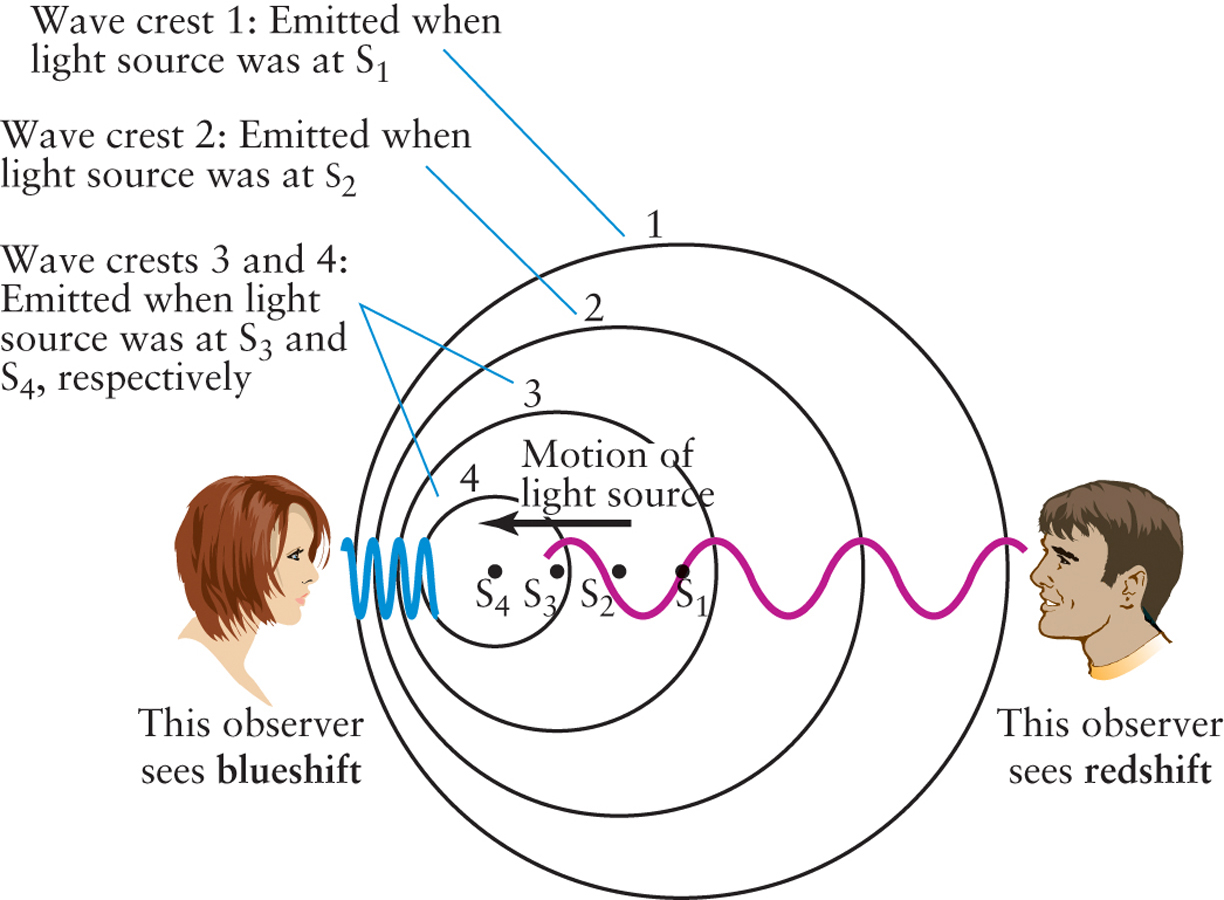
The source is receding from the observer on the right in Figure 2-17. The wave crests that reach him are stretched apart, so that he sees a longer wavelength than he would if the source were stationary. All the lines in the spectrum of a receding source are shifted toward the longer-wavelength (red) end of the spectrum, producing a redshift. In general, the effect of relative motion on wavelength is called the Doppler effect. Some radar guns use the Doppler effect to check for cars exceeding the speed limit: The radar gun sends a radio wave toward the car and measures the wavelength shift of the reflected wave—and thus the speed of the car.
ANALOGY
You have probably noticed a similar Doppler effect for sound waves. When a police car is approaching, the sound waves from its siren have a shorter wavelength and higher frequency than if the moving siren were at rest, and hence you hear a higher pitch. After the police car passes you and is moving away, you hear a lower pitch from the siren because the sound waves have a longer wavelength and a lower frequency.
50
CAUTION
The redshifts and blueshifts of stars visible to the naked eye, or even through a small telescope, are only a small fraction of a nanometer. These tiny wavelength changes are far too small to detect visually. (Astronomers were able to detect the tiny Doppler shifts of starlight only after they had developed highly sensitive equipment for measuring wavelengths. This was done around 1890, a half-century after Doppler’s original proposal.) So, if you see a star with a red color, it means that the star really is red; it does not mean that it is moving rapidly away from us.
The Doppler effect is an important tool in astronomy because it uncovers basic information about the motions of planets, stars, and galaxies. For example, the rotation of the planet Venus was deduced from the Doppler shift of radar waves reflected from its cloud-shrouded surface. Small Doppler shifts in the spectrum of sunlight have shown that the entire Sun is vibrating like an immense gong. The back-and-forth Doppler shifting of the spectral lines of certain stars reveals that these stars are being orbited by unseen companions; from this astronomers have discovered planets around other stars and massive objects that may be black holes. This is only one of many examples of how Doppler’s discovery has empowered astronomers in their quest to understand the universe.
Doppler proved that the wavelength shift (Δλ) is governed by the following simple equation for objects moving at speeds much less than the speed of light:
Doppler shift equation
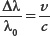
Δλ = wavelength shift
λ0 = wavelength if source is not moving
υ = velocity of the source measured along the line of sight
c = speed of light = 3.0 × 105 km/s
CAUTION
The capital Greek letter Δ, or delta, is commonly used to denote a change in the value of a quantity. Thus, Δλ is the change in the wavelength λ due to the Doppler effect. It is not equal to a quantity Δ multiplied by a second quantity λ.
So far in this chapter we have glimpsed how much can be learned by analyzing light from the heavens. To analyze this light, however, it is first necessary to collect as much of it as possible, because most light sources in space are very dim. Collecting the faint light from distant objects is a key purpose of telescopes.
Question
ConceptCheck 2-11: How is the spectrum changed when looking at an emission spectrum from an approaching cloud of interstellar gas as compared to a stationary cloud?
Question
CalculationCheck 2-4: How fast and in what direction is a star moving if it has a line that shifts from 486.2 nm to 486.3 nm?