3-4 Johannes Kepler proposed that planets orbit the Sun in elliptical paths, moving fastest when closest to the Sun, with the closest planets moving at the highest speeds

Astronomers had long assumed that heavenly objects move in circles, which were considered the most perfect and harmonious of all geometric shapes. Many believed that if a perfect God resided in heaven along with the stars and planets, then the motions of these objects must be perfect, too. At the beginning of the seventeenth century, and against this context, Johannes Kepler took on the task of finding a model of planetary motion that agreed precisely with the observed positions of planets.

Elliptical Orbits and Kepler’s First Law

Kepler was a mathematician and had the unique benefit of access to incredibly precise planetary position data, collected by an eccentric Danish nobleman named Tycho Brahe. Using this data, Kepler dared to try to explain planetary motions with imperfect circles. In particular, he found that he had the best success with a particular shape called an ellipse.

You can draw an ellipse by using a loop of string, two thumbtacks, and a pencil, as shown in Figure 3-14a. Each thumbtack in the figure is at a focus (plural foci) of the ellipse; an ellipse has two foci. The longest diameter of an ellipse, called the major axis, passes through both foci. Half of that distance is called the semimajor axis and is usually designated by the letter a. Another way to think about the distance a is as being the average distance between the edge and a focus point. (A circle is a special case of an ellipse in which the two foci are at the same point. This corresponds to using only a single thumbtack in Figure 3-14a). The semimajor axis, a, of a circle is equal to its radius.

Figure 3-14: Ellipses (a) To draw an ellipse, use two thumbtacks to secure the ends of a piece of string, then use a pencil to pull the string taut. If you move the pencil while keeping the string taut, the pencil traces out an ellipse. The thumbtacks are located at the two foci of the ellipse. The major axis is the greatest distance across the ellipse; the semimajor axis is half of this distance. (b) This shows a series of ellipses with the same major axis but different eccentricities. An ellipse can have any eccentricity from e = 0 (a circle) to just under e = 1 (virtually a straight line).

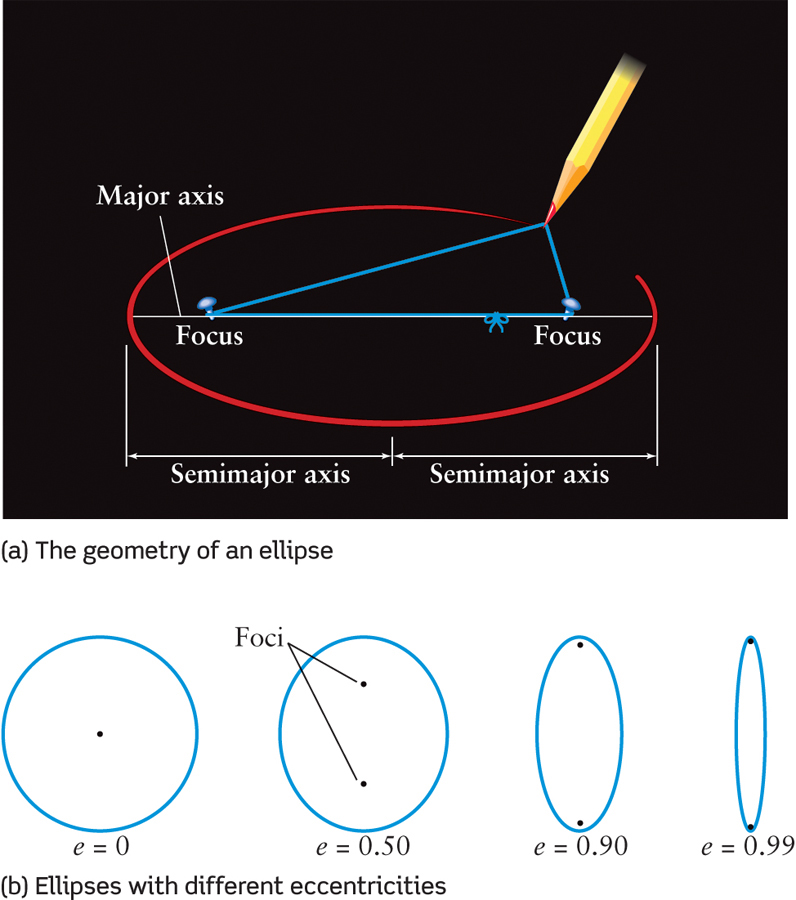
By assuming that planetary orbits are ellipses, Kepler found, to his delight, that he could make his theoretical calculations match precisely to observations. This important discovery, first published in 1609, is now called Kepler’s first law:

The orbit of a planet about the Sun is an ellipse with the Sun at one focus.

The semimajor axis a of a planet’s orbit is the average distance between the planet and the Sun.

Ellipses come in different shapes, depending on the elongation of the ellipse. The shape of an ellipse is described by its eccentricity, designated by the letter e. The value of e can range from 0 (a circle) to just under 1 (nearly a straight line). The greater the eccentricity, the more elongated the ellipse. Figure 3-14b shows a few examples of ellipses with different eccentricities. Because a circle is a special case of an ellipse, it is possible to have a perfectly circular orbit. But all of the objects that orbit the Sun have orbits that are at least slightly elliptical. The most circular of any planetary orbit is that of Venus, with an eccentricity of just 0.007; Mercury’s orbit has an eccentricity of 0.206, and a number of small bodies called comets move in very elongated orbits with eccentricities just less than 1.

Orbital Speeds and Kepler’s Second Law

Once Kepler knew the shape of a planet’s orbit, he was ready to describe exactly how it moves on that orbit. As a planet travels in an elliptical orbit, its distance from the Sun varies. Kepler realized that the speed of a planet also varies along its orbit. A planet moves most rapidly when it is nearest the Sun, at a point on its orbit called perihelion. Conversely, a planet moves most slowly when it is farthest from the Sun, at a point called aphelion (Figure 3-15).

Figure 3-15: Kepler’s First and Second Laws According to Kepler’s first law, a planet travels around the Sun along an elliptical orbit with the Sun at one focus. According to his second law, a planet moves fastest when closest to the Sun (at perihelion) and slowest when farthest from the Sun (at aphelion). As the planet moves, an imaginary line joining the planet and the Sun sweeps out equal areas in equal intervals of time (from A to B or from C to D). By using these laws in his calculations, Kepler found a perfect fit to the apparent motions of the planets.

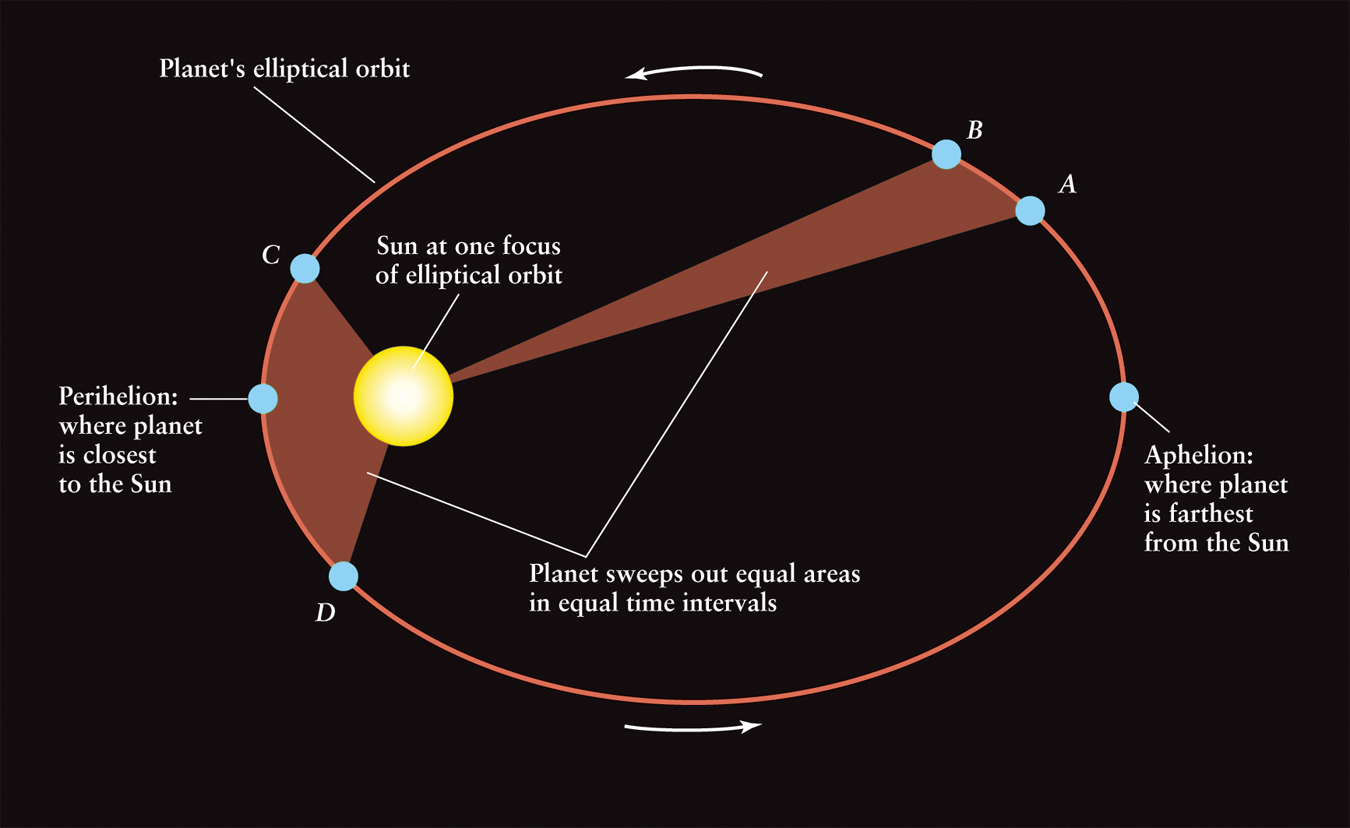
After much trial and error, Kepler found a way to describe just how a planet’s speed varies as it moves along its orbit. Figure 3-15 illustrates this discovery, also published in 1609. Suppose that it takes 30 days for a planet to go from point A to point B. During that time, an imaginary line joining the Sun and the planet sweeps out a nearly triangular area. Kepler discovered that a line joining the Sun and the planet also sweeps out exactly the same area during any other 30-day interval. In other words, if the planet also takes 30 days to go from point C to point D, then the two shaded segments in Figure 3-15 are equal in area. Kepler’s second law can be stated in this way:

A line joining a planet and the Sun sweeps out equal areas in equal intervals of time.

This relationship is also called the law of equal areas. In the idealized case of a circular orbit, a planet would have to move at a constant speed around the orbit in order to satisfy Kepler’s second law.

Orbital Periods and Kepler’s Third Law

Kepler’s second law describes how the speed of a given planet changes as it orbits the Sun. Kepler also deduced a relationship that can be used to compare the motions of different planets. Published later than his first two propositions and now called Kepler’s third law, it states a relationship between the size of a planet’s orbit and the time the planet takes to go once around the Sun:

The square of the sidereal period of a planet is directly proportional to the cube of the semimajor axis of the orbit.

Kepler’s third law says that the larger a planet’s orbit—that is, the larger the semimajor axis, or average distance from the planet to the Sun—the longer the sidereal period, which is the time it takes the planet to complete an orbit. From Kepler’s third law one can show that the larger the semimajor axis, the slower the average speed at which the planet moves around its orbit. (By contrast, Kepler’s second law describes how the speed of a given planet is sometimes faster and sometimes slower than its average speed.) This qualitative relationship between orbital size and orbital speed is just what Aristarchus and Copernicus used to explain retrograde motion. Kepler’s great contribution was to make this relationship a quantitative one.

It is useful to restate Kepler’s third law as an equation. If a planet’s sidereal period P is measured in years and the length of its semimajor axis a is measured in astronomical units (AU), where 1 AU is the average distance from Earth to the Sun, then Kepler’s third law is

Kepler’s third law

We can verify Kepler’s third law for all of the planets, including those that were discovered after Kepler’s death, using data from Table 3-1. If Kepler’s third law is correct, for each planet the numerical values of P² and a³ should be equal. This is indeed true to very high accuracy, as Table 3-2 shows.

The Significance of Kepler’s Laws

Go to Video 3-3

Kepler’s laws are a landmark in the history of astronomy. They made it possible to calculate the motions of the planets with better accuracy than any geocentric model ever had, and they helped to justify the idea of a Sun-centered model. Kepler’s laws also pass the test of Occam’s razor, for they are simpler in every way than the schemes of Ptolemy or Copernicus, both of which used a complicated combination of circles.

But the significance of Kepler’s laws goes far beyond understanding planetary orbits. These same laws are also obeyed by spacecraft orbiting Earth, by two stars revolving about each other in a binary star system, and even by galaxies in their orbits about each other. Throughout this book, we will use Kepler’s laws in a wide range of situations.

As impressive as Kepler’s mathematical accomplishments were in describing when planets could be found where in the sky, he did not prove that the planets orbit the Sun, nor was he able to explain why planets move in accordance with his three laws. While we attribute the demonstration that planets orbit the Sun to Galileo, who worked independently from Kepler, Isaac Newton is credited as the luminary who figured out that gravity was responsible for why the planets move as they do.