3-6 Newton’s description of gravity accounts for Kepler’s laws and explains the motions of the planets

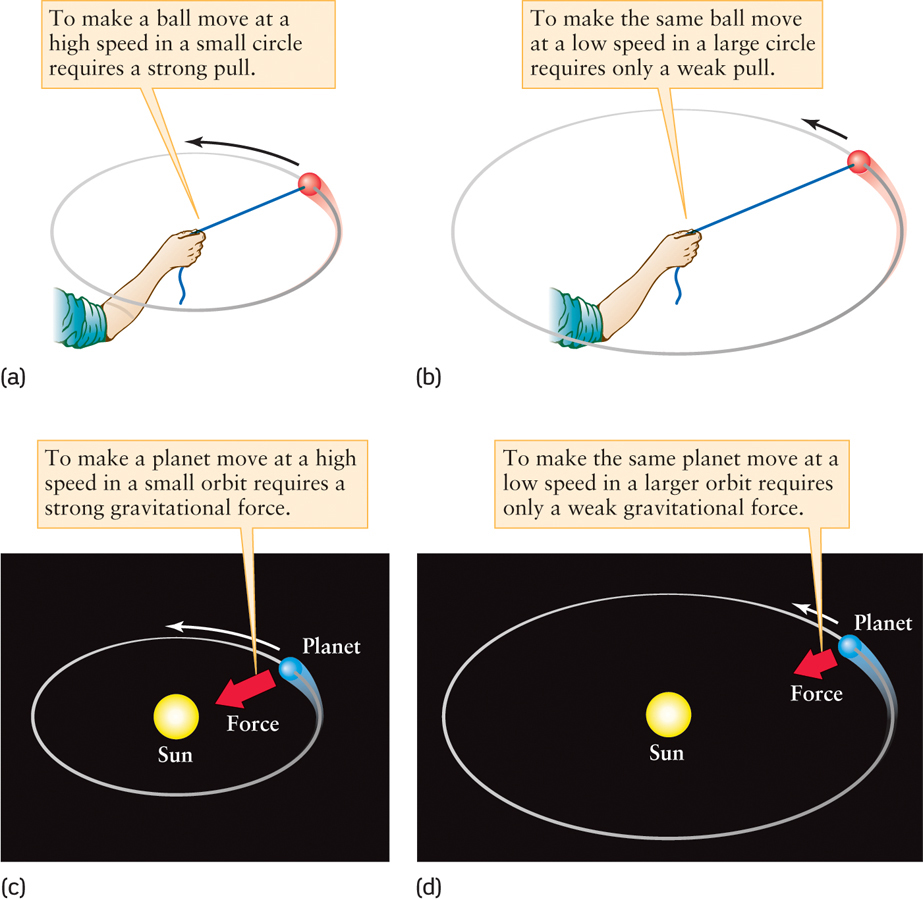
Tie a ball to one end of a piece of string, hold the other end of the string in your hand, and whirl the ball around in a circle. As the ball “orbits” your hand, it is continuously accelerating because its velocity is changing. (Even if its speed is constant, its direction of motion is changing.) In accordance with Newton’s second law, this can happen only if the ball is continuously acted on by an outside force—the pull of the string. The pull is directed along the string toward your hand. In the same way Newton saw the gravitational attractions between the planets and the Sun act as a pull toward the significantly more massive Sun. That pull is gravity, or gravitational force.

Newton’s discovery about the forces that act on planets led him to suspect that the force of gravity pulling a falling apple straight down to the ground is fundamentally the same as the force on a planet that is always directed straight at the Sun. In other words, gravity is the force that shapes the orbits of the planets. What is more, he was able to determine how the gravitational attractions between the planets and the Sun depend on the distances between them. His result was a law of gravitation that could apply to the motion of distant planets as well as to the flight of a soccer ball on Earth. Using this law, Newton achieved the remarkable goal of deducing Kepler’s laws from fundamental principles of nature.

To see how Newton reasoned, think again about a ball attached to a string. If you use a short string, so that the ball orbits in a small circle, and whirl the ball around your hand at a high speed, you will find that you have to pull fairly hard on the string (Figure 3-16a). But if you use a longer string, so that the ball moves in a larger orbit, and if you make the ball orbit your hand at a slow speed, you only have to exert a light tug on the string (Figure 3-16b). The orbits of the planets behave in the same way; the larger the size of the orbit, the slower the planet’s speed (Figure 3-16c, d). By analogy to the force of the string on the orbiting ball, Newton concluded that the force that attracts a planet toward the Sun must decrease with increasing distance from the Sun.

The Law of Universal Gravitation

Using his own three laws and Kepler’s three laws, Newton succeeded in formulating a general statement that describes the nature of the gravitational force. Newton’s law of universal gravitation is as follows:

Two objects attract each other with a force that is directly proportional to the mass of each object and inversely proportional to the square of the distance between them.

This law states that any two objects exert gravitational pulls on each other. Normally, you notice only the gravitational force that Earth exerts on you, otherwise known as your weight. In fact, you feel gravitational attractions to all the objects around you. For example, this book is exerting a gravitational force on you as you read it. But because the force exerted on you by this book is proportional to the book’s mass, which is very small compared to Earth’s mass, the force is too small to notice. (It can actually be measured with sensitive equipment.)

Consider two 1-kg objects separated by a distance of 1 m. Newton’s law of universal gravitation says that the force is directly proportional to the mass, so if we double the mass of one object to 2 kg, the force between the objects will double. If we double both masses so that we have two 2-kg objects separated by 1 m, the force will be 2 × 2 = 4 times what it was originally (the force is directly proportional to the mass of each object). If we go back to two 1-kg masses, but double their separation to 2 m, the force will be only one-quarter its original value. This is because the force is inversely proportional to the square of the distance: If we double the distance, the force is multiplied by a factor of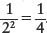

Newton’s law of universal gravitation can be stated more succinctly as an equation. If two objects have masses m₁ and m₂ and are separated by a distance r, then the gravitational force F between these two objects is given by the following equation:

Newton’s law of universal gravitation

If the masses are measured in kilograms and the distance between them in meters, then the force is measured in newtons. In this formula, G is a number called the universal constant of gravitation. Laboratory experiments have yielded a value for G of

We can use Newton’s law of universal gravitation to calculate the force with which any two objects attract each other. For example, to compute the gravitational force that the Sun exerts on Earth, we substitute values for Earth’s mass (m₁ = 5.98 × 10²⁴ kg), the Sun’s mass (m₂ = 1.99 × 10³⁰ kg), the distance between them (r = 1 AU = 1.5 × 10¹¹ m), and the value of G into Newton’s equation. We get

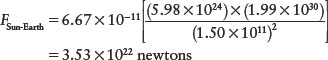
If we calculate the force that Earth exerts on the Sun, we get exactly the same result. (Mathematically, we just let m₁ be the Sun’s mass and m₂ be Earth’s mass instead of the other m₂ way around. The product of the two numbers is the same, so the force is the same.) This is in accordance with Newton’s third law: Any two objects exert equal gravitational forces on each other.

Your weight is just the gravitational force that Earth exerts on you, so we can calculate it using Newton’s law of universal gravitation. Earth’s mass is m₁ = 5.98 × 10²⁴ kg, and the distance r is the distance between the centers of Earth and you. This is just the radius of Earth, which is r = 6378 km = 6.378 × 10⁶ m. If your mass is m₂ = 50 kg, your weight is

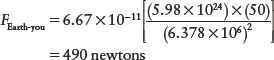
This is the same as the weight of a 50-kg person that we calculated earlier. This example shows that your weight would have a different value on a planet with a different mass m₁ and a different radius r.

Gravitational Force and Orbits

Go to Video 3-4

Because there is a gravitational force between any two objects, Newton concluded that gravity is also the force that keeps the Moon in orbit around Earth. It is also the force that keeps artificial satellites in orbit. But if the force of gravity attracts two objects to each other, why don’t satellites immediately fall to Earth? Why doesn’t the Moon fall into Earth? And, for that matter, why don’t the planets fall into the Sun?

Let’s conduct an imaginary experiment. Suppose you were to imagine dropping a ball from a great height above Earth’s surface, as in Figure 3-17. After you drop the ball, it, of course, falls straight down (path A in Figure 3-17). But if you throw the ball horizontally, it travels some distance across Earth’s surface before hitting the ground (path B). If you throw the ball harder, it travels a greater distance (path C). If you could throw at just the right speed, the curvature of the ball’s path will exactly match the curvature of Earth’s surface (path E). Although Earth’s gravity is making the ball fall, Earth’s surface is moving away under the ball at the same rate. Hence, the ball does not get any closer to the surface, and we would say that “the ball is in circular orbit.” So the ball in path E is in fact falling, but it is falling around Earth rather than toward Earth.

A spacecraft is launched into orbit in just this way—by shooting it fast enough. The thrust of a rocket is used to give the spacecraft the necessary orbital speed. Once the spacecraft is in orbit, the rocket engines are turned off and the spacecraft falls continually around Earth.

If the ball in Figure 3-17 is thrown with a slightly slower speed than that required for a circular orbit, its orbit will be an ellipse (path D). An elliptical orbit also results if instead the ball is thrown a bit too fast (path F). In this way, spacecraft can be placed into any desired orbit around Earth by adjusting the initial rocket thrust.

Just as the ball in Figure 3-17 will not fall to Earth if given enough speed, the Moon does not fall to Earth and the planets do not fall into the Sun. The planets acquired their initial speeds around the Sun when the solar system first formed 4.56 billion years ago. Figure 3-17 shows that a circular orbit is a very special case, so it is no surprise that the orbits of the planets are not precisely circular.