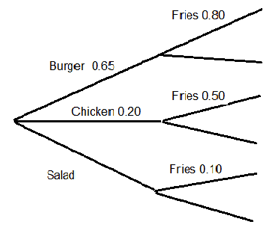
StatTutor Lesson - Tree Diagrams
true
Stat Tutor
true
true
You have completed 0 question sequences out of 3.
Questions 1-4
129
Question 1.
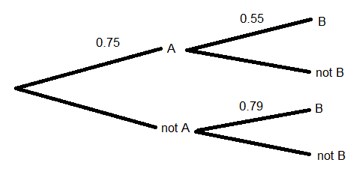
In the tree diagram below, what is the probability of B if event A does not happen?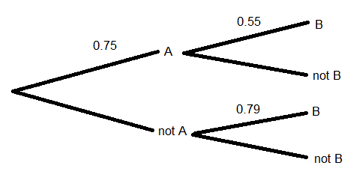
| A. |
| B. |
| C. |
| D. |
Correct. If event A does not happen, we are on the lower set of branches. We can read that the probability of B happening in that case is 0.25.
Incorrect. If event A does not happen, we are on the lower set of branches. We can read that the probability of B happening in that case is 0.25.
2
Try again.
Questions 5-8
189
Question 5.
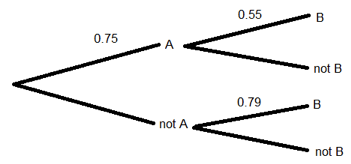
In the tree diagram above, what is the probability events A and B both happen?
Correct. This is a joint probability; we find those by multiplying out the branches of the tree. Here, P(A and B) = 0.75*0.55.
Incorrect. This is a joint probability; we find those by multiplying out the branches of the tree. Here, P(A and B) = 0.75*0.55.
2
Try again.
Questions 9-10
409
Question 9.
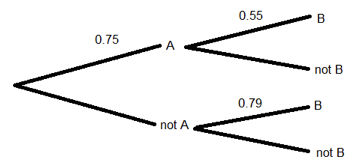
In the tree diagram above, what is the probability event B happens?
| A. |
| B. |
| C. |
| D. |
Correct. To find the probability event B happens, we need to multiply out the two branches that end with B and add those together. We have 0.75*0.55 + (1 – 0.75)*0.79.
Incorrect. To find the probability event B happens, we need to multiply out the two branches that end with B and add those together. We have 0.75*0.55 + (1 – 0.75)*0.79.
2
Try again.