StatTutor Lesson - Independence Again
true
Stat Tutor
true
true
You have completed 0 question sequences out of 3.
Questions 1-3
315
Question 1.
What is the probability of a face card in a deck? Enter your answer as a fraction in lowest terms.
Correct. The face cards in a deck are the Jack, Queen, and King for each of the four suits. There are 12 face cards in the deck of 52, so the probability is 12/52, or 4/13 in lowest terms.
Incorrect. The face cards in a deck are the Jack, Queen, and King for each of the four suits. There are 12 face cards in the deck of 52, so the probability is 12/52, or 4/13 in lowest terms.
2
Try again.
Questions 4-5
406
Question 4.
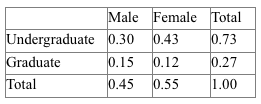
Consider the gender and class make-up of students at a large university by gender and status as shown in the table above. What is P(Female | Undergraduate)? Give your answer to three decimal places.
Correct. P(Female | Undergraduate) = P(Female and Undergraduate)/P(Undergraduate) = 0.43/0.73.
Incorrect. P(Female | Undergraduate) = P(Female and Undergraduate)/P(Undergraduate) = 0.43/0.73.
2
Try again.
Questions 6-7
619
Question 6.
Consider weather forecasting. The weather bureau says the high temperature for tomorrow will be 70°F. You are hoping for snow. Are those events disjoint, independent, or neither?
| A. |
| B. |
| C. |
Correct. Because it takes temperatures at or below the freezing level (32°F) for snow, these events are disjoint. Knowing the temperature will be this high makes snow impossible.
Incorrect. Because it takes temperatures at or below the freezing level (32°F) for snow, these events are disjoint. Knowing the temperature will be this high makes snow impossible.
2
Try again.