{0.30, 0.35, 0.40, 0.45, 0.50}
{0.70, 0.65, 0.60, 0.55, 0.50}
rand(0,4)
0.5[4]
0.70, 0.65, 0.60, 0.55, 0.50[4]
{0.084, 0.078, 0.072, 0.066, 0.060}
0.084, 0.078, 0.072, 0.066, 0.060[4]
{0.126, 0.147, 0.168, 0.189, 0.21}
{0.874, 0.853, 0.832, 0.811, 0.79}
{0.084, 0.078, 0.072, 0.066, 0.06}
{0.916, 0.922, 0.928, 0.934, 0.94}
0.126, 0.147, 0.168, 0.189, 0.21[4]
0.874, 0.853, 0.832, 0.811, 0.79[4]
0.084, 0.078, 0.072, 0.066, 0.06[4]
0.916, 0.922, 0.928, 0.934, 0.94[4]
{80, 85, 90, 95}
rand(0,3)
90[2]
{0.072, 0.053, 0.034, 0.017}
{0.928, 0.947, 0.966, 0.983}
{0.415, 0.469, 0.535, 0.632}
{0.585, 0.531, 0.464, 0.368}
0.072, 0.053, 0.034, 0.017[2]
0.928, 0.947, 0.966, 0.983[2]
0.415, 0.469, 0.535, 0.632[2]
0.585, 0.531, 0.464, 0.368[2]
{0.30, 0.35, 0.40, 0.45, 0.50}
{0.70, 0.65, 0.60, 0.55, 0.50}
rand(0,4)
0.35[1]
0.70, 0.65, 0.60, 0.55, 0.50[1]
0.35[1]
{0.084, 0.078, 0.072, 0.066, 0.060}
0.084, 0.078, 0.072, 0.066, 0.060[1]
0.35[1]
{0.126, 0.147, 0.168, 0.189, 0.21}
{0.874, 0.853, 0.832, 0.811, 0.79}
{0.084, 0.078, 0.072, 0.066, 0.06}
{0.916, 0.922, 0.928, 0.934, 0.94}
0.126, 0.147, 0.168, 0.189, 0.21[1]
0.874, 0.853, 0.832, 0.811, 0.79[1]
0.084, 0.078, 0.072, 0.066, 0.06[1]
0.916, 0.922, 0.928, 0.934, 0.94[1]
{80, 85, 90, 95}
rand(0,3)
1[2]
{0.072, 0.053, 0.034, 0.017}
{0.928, 0.947, 0.966, 0.983}
{0.415, 0.469, 0.535, 0.632}
{0.585, 0.531, 0.464, 0.368}
0.072, 0.053, 0.034, 0.017[2]
0.928, 0.947, 0.966, 0.983[2]
0.415, 0.469, 0.535, 0.632[2]
0.585, 0.531, 0.464, 0.368[2]
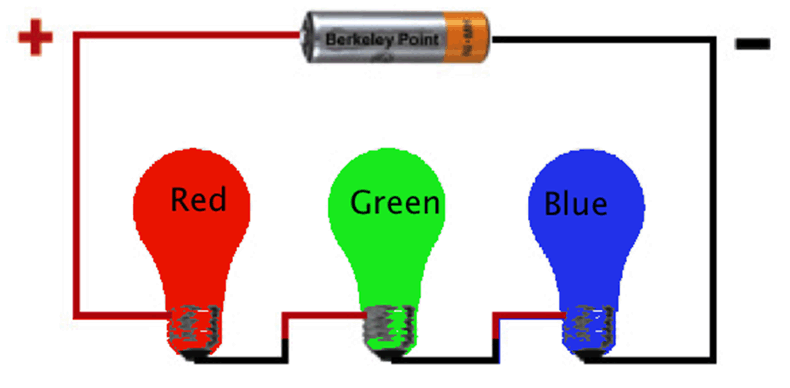
Series circuits have the components on the same line and if any one fails, the entire circuit does not work (similar to old fashion Christmas lights). Consider the series circuit below with different colored lights. The probability that a bulb fails during the holiday season varies by color with P(failure for red) = 0.5 ; P(failure for green)=0.60; P(failure for blue) = 0.70. Each bulb fails independently of the other bulbs.