THEOREM A Limit Is Unique

If a function \(f\) is defined on an open interval containing the number \(c\), except possibly at \(c\) itself, and if \(\lim\limits_{x\rightarrow c}f( x) = L_{1}\) and \(\lim\limits_{x\rightarrow c}f(x) = L_{2},\) then \(L_{1} = L_{2}.\)

Recall

An indirect proof (a proof by contradiction) begins by assuming the conclusion is false. Then we show that this assumption leads to a contradiction.

Proof

Assume that \(L_{1}\neq L_{2}\). We will show that this assumption leads to a contradiction. By the definition of the limit of a function \(f,\) \(\lim\limits_{x\rightarrow c}f(x) = L_{1}\) if, for any given number \(\varepsilon > 0\), there is a number \(\delta _{1} > 0\), so that \begin{equation} {\rm whenever}\ 0 < \vert x-c\vert < \delta_{1}\quad {\rm then}\ \vert f(x)-L_{1}\vert < \varepsilon\tag{1} \end{equation}

Similarly, \(\lim\limits_{x\rightarrow c}f(x) = L_{2}\) if, for any given number \(\varepsilon > 0\), there is a number \(\delta_{2} > 0\), so that \begin{equation} {\rm whenever}\ 0 < \vert x-c\vert < \delta_{2}\quad {\rm then }\ \vert f(x)-L_{2}\vert < \varepsilon\tag{2} \end{equation}

Now \begin{equation*} L_{1} - L_{2} = L_{1}-f(x) + f(x)-L_{2} \end{equation*}

so, by applying the Triangle Inequality, we get \begin{equation} \vert L_{1}-L_{2}\vert = \vert L_{1}-f(x)+f(x)-L_{2}\vert \leq \vert L_{1}-f(x)\vert + \vert f(x)-L_{2}\vert\tag{3} \end{equation}

For any given number \(\varepsilon > 0\), let \(\delta \) be the smaller of \(\delta _{1}\) and \(\delta _{2}.\) Then from (1)–(3), we can conclude that whenever \(0 < \vert x-c \vert < \delta \leq \delta_{1}\) and \(0 < \vert x-c\vert < \delta \leq \delta _{2}\), we have \begin{equation} \vert L_{1}-L_{2}\vert < \varepsilon +\varepsilon = 2 \varepsilon \tag{4} \end{equation}

In particular, (4) is true for \(\varepsilon =\dfrac{1}{2}\vert L_{1}-L_{2}\vert >0\). (Remember \(L_{1}\neq L_{2}\).) Then from (4), \begin{equation*} \vert L_{1}-L_{2}\vert < 2\varepsilon = \vert L_{1}-L_{2}\vert \end{equation*}

which is a contradiction. Therefore, \(L_{1}=L_{2}\), and the limit, if it exists, is unique.

THEOREM Limit of a Sum

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f( x) \) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist, then \(\lim\limits_{x\rightarrow c}\,[f(x)+g(x)]\) exists and \[ \lim\limits_{x\rightarrow c}[f(x)+g(x)]=\lim\limits_{x\rightarrow c}f(x)+\lim\limits_{x\rightarrow c}g(x) \]

Proof

Suppose \(\lim\limits_{x\rightarrow c}f(x)=L\) and \(\lim\limits_{x\rightarrow c}g(x)=M.\) We need to show that for any number \(\varepsilon > 0,\) there is a number \(\delta > 0,\) so that \begin{equation*} {\rm whenever}\ 0 < \vert x-c\vert < \delta\quad {\rm then}\ \vert [ f(x)+g(x)] - [ L+M] \vert < \varepsilon \end{equation*}

Since \(\lim\limits_{x\rightarrow c}f(x)\) \(=L\), by the definition of a limit, given the number \(\dfrac{\varepsilon }{2} > 0\), there is a number \(\delta_{1} > 0\), so that \begin{equation*} {\rm whenever}\ 0 < \vert x-c\vert < \delta_{1}\quad {\rm then}\ \vert f(x)-L\vert < \dfrac{\varepsilon }{2} \end{equation*}

Since \(\lim\limits_{x\rightarrow c}g(x)=M\), for this same number \(\dfrac{\varepsilon }{2},\) there is a number \(\delta _{2} > 0,\) so that \begin{equation*} {\rm whenever}\ 0 < \vert x-c\vert < \delta _{2}\quad {\rm then}\ \vert g(x)-M\vert < \dfrac{\varepsilon }{2} \end{equation*}

Let \(\delta \) be the smaller of \(\delta _{1}\) and \(\delta _{2}\). Then \(\delta \leq \delta _{1}\) and \(\delta \leq \delta _{2}\). Using this \(\delta\), \begin{eqnarray*} {\rm whenever}\ 0 & < \vert x-c\vert <\delta\quad {\rm then}\ \vert f(x)-L\vert < \dfrac{\varepsilon }{2} \\[4.5pt] {\rm whenever}\ 0 & < \vert x-c\vert < \delta\quad {\rm then}\ \vert g(x)-M\vert < \dfrac{\varepsilon }{2} \end{eqnarray*}

That is, whenever \(0 < \vert x-c\vert < \delta,\) \begin{eqnarray*} \begin{array}{ll} \vert [ f(x)+g(x)] -[ L+M]\vert & = \vert [ f(x)-L] + [ g(x)-M] \vert \\[4pt] & \leq \vert f(x)-L\vert + \vert g(x)-M \vert\quad {\color{#0066A7}{\hbox{Use the Triangle Inequality.}}} \\[4pt] & < \dfrac{\varepsilon}{2} + \dfrac{\varepsilon }{2} = \varepsilon \end{array}\end{eqnarray*}So, \(\lim\limits_{x\rightarrow c} [ f(x)+g(x)] =L+M\).

THEOREM Limit of a Product

If \(f\) and \(g\) are functions for which \(\lim\limits_{x\rightarrow c}f(x)\) and \(\lim\limits_{x\rightarrow c}g(x)\) both exist,
then \(\lim\limits_{x\rightarrow c}\,[f(x)\cdot g(x)]\) exists and \begin{eqnarray*} \lim\limits_{x\rightarrow c}\,[f(x)\cdot g(x)]=\lim\limits_{x\rightarrow c}f(x)\cdot \lim\limits_{x\rightarrow c}g(x) \end{eqnarray*}

Proof

Suppose \(\lim\limits_{x\rightarrow c}f(x) = L\) and \( \lim\limits_{x\rightarrow c}g(x) = M.\) We need to show that for any number \( \varepsilon > 0,\) there is a number \(\delta > 0\), so that \begin{equation*} {\rm whenever}\ 0 < \vert x-c\vert < \delta\quad {\rm then}\ \vert f(x)\cdot g(x)-L\cdot M\vert < \varepsilon \end{equation*}

Subtracting and adding \(f(x)\cdot M\) in the expression \(f(x)\cdot g(x)-L\cdot M\) result in terms involving \(g(x)-M\) and \(f(x)-L\):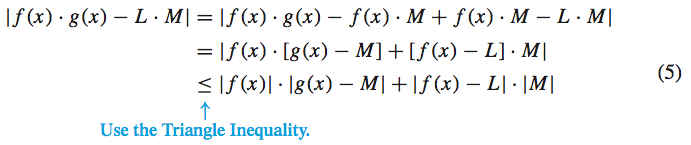

Since \(\lim\limits_{x\rightarrow c}f(x)=L\) and \(\lim\limits_{x\rightarrow c}g(x)=M\), then there is a number \(\delta _{1} > 0\), so that whenever \( 0 < \vert x-c\vert <\delta _{1}\), then \begin{equation} \vert f(x)-L\vert < 1, \qquad \hbox{from which}\qquad \vert f(x)\vert < 1 + \vert L\vert\tag{6} \end{equation}

Also given a number \(\varepsilon >0\), there is a number \(\delta _{2}\), so that whenever \(0 < \vert x-c\vert < \delta_{2}\), then \begin{equation} \vert g(x)-M\vert < \dfrac{\varepsilon }{1+ \vert L\vert +\vert M\vert }\tag{7} \end{equation}

Given a number \(\varepsilon >0\), there is a number \(\delta _{3}\), so that whenever \(0 < \vert x-c \vert <\delta _{3}\), then \begin{equation} \vert f(x)-L\vert <\dfrac{\varepsilon }{1+\vert L\vert +\vert M\vert }\tag{8} \end{equation}

Choose \(\delta \) to be the minimum of \(\delta _{1},\) \(\delta _{2},\) and \( \delta _{3}\) and combine (5)–(8). Then for any given \( \varepsilon >0,\) there is a \(\delta >0\), so that whenever \(0 < \vert x-c\vert <\delta\), we have \begin{eqnarray*} \vert f(x)\cdot g(x)-L\cdot M\vert & < & [ 1 + \vert L\vert ] \dfrac{\varepsilon }{1 + \vert L\vert + \vert M\vert } + \vert M\vert \dfrac{\varepsilon }{ 1 + \vert L\vert + \vert M\vert } \\[4pt] & < & [ 1 + \vert L\vert + \vert M\vert ] \dfrac{ \varepsilon }{1 + \vert L\vert + \vert M\vert } =\varepsilon \end{eqnarray*}

That is, \(\lim\limits_{x\ c}\,[f(x)\cdot g(x)]=\lim\limits_{x\rightarrow c}f(x)\cdot \lim\limits_{x\rightarrow c}g(x).\)

THEOREM Squeeze Theorem

If the functions \(f\), \(g\), and \(h\) have the property that for all \(x\) in an open interval containing \(c\), except possibly at \(c\) itself, \[ f(x)\leq g(x)\leq h(x) \] and if \[ \lim_{x\rightarrow c}f(x) = \lim_{x\rightarrow c}h(x) = L \] then \[ \lim_{x\rightarrow c}g(x) = L \]

Proof

Since \(\lim\limits_{x\rightarrow c}f(x) = \lim\limits_{x\rightarrow c}h(x) = L,\) then for any number \(\varepsilon > 0\), there are positive numbers \(\delta _{1}\) and \(\delta _{2}\), so that \begin{eqnarray*} {\rm whenever}\ 0 & < \vert x-c \vert < \delta_{1}\quad \hbox{then } \vert f(x)-L \vert < \varepsilon\\ {\rm whenever}\ 0 & < \vert x-c\vert < \delta_{2}\quad \hbox{then } \vert h(x)-L \vert < \varepsilon \end{eqnarray*}

Choose \(\delta\) to be the smaller of the numbers \(\delta_{1}\) and \(\delta_{2}\). Then \(0 < \vert x-c\vert < \delta\) implies that both \(\vert f(x)-L \vert < \varepsilon\) and \(\vert h(x)-L \vert < \varepsilon\). In other words, \(0 < \vert x-c \vert < \delta\) implies that both \begin{equation*} L - \varepsilon < f(x) < L + \varepsilon\qquad \hbox{and}\qquad L - \varepsilon < h(x) < L + \varepsilon \end{equation*}

Since \(f(x)\leq g(x)\leq h(x)\) for all \(x\neq c\) in the open interval, it follows that whenever \(0 < \vert x-c\vert < \delta\) and \(x\) is in the open interval, we have \begin{equation*} L - \varepsilon < f(x) \leq g(x) \leq h(x) < L + \varepsilon \end{equation*}

Then for any given number \(\varepsilon >0\), there is a positive number \(\delta \), so that whenever \(0 < \vert x-c\vert < \delta,\) then \(L - \varepsilon < g(x) < L + \varepsilon\), or equivalently, \(\vert g(x) -L\vert < \varepsilon.\) That is, \(\lim\limits_{x\rightarrow c}g(x) = L.\)