10.5 Assess Your UnderstandingPrinted Page 730
Concepts and Vocabulary
True or False The direction of v×w is determined by the right-hand rule.
True
True or False Since i and j are orthogonal, i×j=0.
False
Multiple Choice The cross product v×w is [(a) parallel, (b) orthogonal] to the vector v and to the vector w.
(b)
True or False The cross product is a commutative operation.
False
Multiple Choice If u and v are parallel, then u×v=[(a)i,(b)j,(c)k,(d)0].
(d)
True or False If v and w are two nonzero vectors, then (v×w)+(w×v)=0.
True
Multiple Choice The area of a parallelogram having vectors v and w as adjacent sides equals [(a) ‖, (b) \left\Vert\mathbf{v \,{ \cdot}\, w}\right\Vert, (c) \left\Vert\mathbf{v \times w}\right\Vert].
(c)
True or False If \theta is the angle between two nonzero vectors \mathbf{v} and \mathbf{w}, then \left\Vert \mathbf{ v\times w}\right\Vert =\left\Vert \mathbf{v}\right\Vert \left\Vert \mathbf{w} \right\Vert \cos \theta .
False
Skill Building
In Problems 9–12, find the value of each determinant.
\left|\begin{array}{r@{\quad}r} 3 & 4 \\[3pt] 1 & 2 \end{array}\right|
2
\left|\begin{array}{r@{\quad}r} -2 & 4 \\[3pt] 2 & -1 \end{array}\right|
\left|\begin{array}{r@{\quad}r@{\quad}r} 1 & -2 & 2 \\ 1 & 2 & 1 \\ 2 & 1 & 4 \end{array}\right|
5
\left|\begin{array}{l@{\quad}l@{\quad}l} 7 & 0 & 1 \\[3pt] 0 & 2 & 3 \\[3pt] 0 & 1 & 3 \end{array}\right|
In Problems 13–22:
- (a) Find the cross product \bf v \times w .
- (b) Check your answer by showing that {\bf v} and {\bf w} are each orthogonal to {\bf v\times w}.
731
\mathbf{v}=2\mathbf{i}+\mathbf{j}-\mathbf{k}, \mathbf{w}=\mathbf{i}-\mathbf{j}+\mathbf{k}
- (a) -3\mathbf{j}-3\mathbf{k}
- (b) See Student Solutions Manual.
\mathbf{v}=4\mathbf{i}-\mathbf{j}+2\mathbf{k}, \mathbf{w}=2\mathbf{i}+\mathbf{j}+\mathbf{k}
\mathbf{v}=\mathbf{i}+\mathbf{j}, \mathbf{w}=\mathbf{i}-\mathbf{k}
- (a) -\mathbf{i}+\mathbf{j}-\mathbf{k}
- (b) See Student Solutions Manual.
\mathbf{v}=\mathbf{j}-\mathbf{k}, \mathbf{w}=\mathbf{i}-\mathbf{j}
\mathbf{v}=3\mathbf{i}-2\mathbf{j}+\mathbf{k}, \mathbf{w}=\mathbf{i}+\mathbf{j}
- (a) -\mathbf{i}+\mathbf{j}+5\mathbf{k}
- (b) See Student Solutions Manual.
\mathbf{v}=2\mathbf{i}-\mathbf{j}, \mathbf{w}=\mathbf{i}+\mathbf{j}-3\mathbf{k}
\mathbf{v}=-\mathbf{i}+8\mathbf{j}+3\mathbf{k}, \mathbf{w}=7\mathbf{i}+2\mathbf{j}
- (a) -6\mathbf{i}+21\mathbf{j}-58\mathbf{k}
- (b) See Student Solutions Manual.
\mathbf{v}=2\mathbf{j}-\mathbf{k}, \mathbf{w}=-3\mathbf{i}+\mathbf{j}+\mathbf{k}
\mathbf{v}=2\mathbf{i}+3\mathbf{j}-4\mathbf{k}, \mathbf{w}=-\mathbf{i}+\mathbf{j}-4\mathbf{k}
- (a) -8\mathbf{i}+12\mathbf{j}+5\mathbf{k}
- (b) See Student Solutions Manual.
\mathbf{v}=(\cos \theta )\,\mathbf{i}-(\sin \theta )\,\mathbf{j}, \mathbf{w}=(\sin \theta )\,\mathbf{i}+(\cos \theta )\,\mathbf{j}
In Problems 23–34, \mathbf{u}=2 \mathbf{i}+3 \mathbf{j}-4 \mathbf{k}, \mathbf{v}=-3 \mathbf{i}+ \mathbf{j}-4 \mathbf{k}, \mathbf{w= i + j}-3 {\bf k}. Find the following.
\mathbf{u\times u}
\mathbf{0}
\mathbf{w} \times \mathbf{w}
\mathbf{v\times w}
\mathbf{i}-13\mathbf{j}-4\mathbf{k}
\mathbf{u\times v}
( 3\mathbf{v}) \times {\bf w}
3\mathbf{i}-39\mathbf{j}-12\mathbf{k}
\mathbf{u} \mathbf{\times \,} ( -\mathbf{v})
a vector orthogonal to both \mathbf{v} and \mathbf{w}
\mathbf{i}-13\mathbf{j}-4\mathbf{k}; Answers will vary.
a vector orthogonal to both \mathbf{w} and \mathbf{u}
a vector orthogonal to both \mathbf{w} and \mathbf{i+j-k}
2\mathbf{i}-2\mathbf{j}; Answers will vary.
a vector orthogonal to both \mathbf{u} and \mathbf{k}
a unit vector normal to the plane containing \mathbf{u} and \mathbf{v}
-\dfrac{8}{3\sqrt{65}}\mathbf{i}+\dfrac{20}{3\sqrt{65}}\mathbf{j}+\dfrac{11}{3\sqrt{65}}\mathbf{k}, the opposite of the given vector is also correct
a unit vector normal to the plane containing \mathbf{u} and \mathbf{w}
Find a unit vector normal to the plane containing \mathbf{v} =2\mathbf{i}-6\mathbf{j}-3\mathbf{k} and \mathbf{w}=4\mathbf{i}+3\mathbf{j}-\mathbf{k}.
\dfrac37\mathbf{i}-\dfrac27\mathbf{j}+\dfrac67\mathbf{k}, the opposite of the given vector is also correct
Find a unit vector normal to the plane containing \mathbf{v}= \mathbf{i}+\mathbf{j}-2\mathbf{k} and \mathbf{w}=3\mathbf{i}+2\mathbf{j}- \mathbf{k}.
Area of a Parallelogram In Problems 37–42, find the area A of the parallelogram with one corner at P and sides PQ and PR.
P=(1,-3, 7); \qquad Q=(2, 1, 1); \quad R=(6,-1, 2)
\sqrt{1013}
P=(0, 1, 1);\quad Q=(2, 0,-4); \quad R=(-3,-2, 1)
P=(-2, 1, 6);\quad Q=(2, 1,-7);\quad R=(4, 1, 1)
58
P=(0, 0, 3);\quad Q=(2,-5, 3);\quad R=(1, 1,-2)
P=(1, 1,-6);\quad Q=(5,-3, 0);\quad (R=(-2, 4, 1)
46\sqrt{2}
P=(-4, 6, 3);\quad Q=(1, 1,-5);\quad R=(2, 2, 2)
Area of a Parallelogram In Problems 43–46, find the area of the parallelogram whose vertices are P_{1}, P_{2}, P_{3}, and P_{4}.
P_{1}=(0, 0, 0);\quad P_{2}=(1, 2, 3); \quad P_{3}=(3, 1, 4); \quad P_{4}=(2,-1, 1)
5\sqrt{3}
P_{1}=(0, 0, 0);\quad P_{2}=(-1, 2, 0); \quad P_{3}=(1, 5,-4); \quad P_{4}=(2, 3,-4)
P_{1}=(-2, 1,6); \quad P_{2}=(2, 1, -7);\quad P_{3}=(4, 1, 1);\quad P_{4}=(8,1, -12)
58
P_{1}=(-1, 1, 1);\quad P_{2}=(-1, 2, 2);\quad P_{3}=(-3, 5, -4);\quad P_{4}=(-3, 4, -5)
Applications and Extensions
Angular Velocity A rigid body rotates about an axis through the origin with a constant angular speed of 30 radians per second. The angular velocity {\omega } points in the direction of \mathbf{i}+\mathbf{j}+\mathbf{k}. Find the speed of an object at the instant it passes through the point (-1,2,3). Assume the distance scale is in meters.
10\sqrt{78} m/s
Angular Velocity A rigid body rotates with constant angular speed \omega about a line through the origin parallel to 3\mathbf{i}+ \mathbf{j}-2\mathbf{k}.
- (a) Find the speed of an object at the instant that it passes through the point (4,4,0). Assume that distance is measured in meters.
- (b) Find \omega if the speed of the object at the point (4,4,0) is 8 \sqrt{14}~\text{m}/\text{s}.
Area of a Triangle Show that the area of the triangle whose vertices are the endpoints of the vectors \mathbf{u}, \mathbf{v}, and \mathbf{w} is A=\dfrac{1}{2}\left\| (\mathbf{v}-\mathbf{u})\times ( \mathbf{w}-\mathbf{u})\right\|
See Student Solutions Manual.
Area of a Triangle Use the result of Problem 49 to find the area of the triangle with vertices (0,0,0), (2,3,-2), and (-1,1,4).
Problems 51 and 52 use the following discussion. When a force \mathbf{F} acts on an object at some distance r from a point P, called the pivot point, it can cause the object to rotate rather than translate. The ability of a force to cause rotation is called the torque about P due to the force {\bf F} and is symbolized by the Greek lowercase letter tau {\tau }. Torque equals the cross product between the applied force {\bf F} and the distance vector {\bf r}= \overrightarrow\rm{PQ} that points from P to the point Q where {\bf F} acts on the object. That is, \tau = {\bf r} \times {\bf F}
Using a Wrench The figure below shows a wrench that is being used to turn a nut and three separate forces that could be applied to the end of the wrench. The point P is at the origin of the coordinate system and the point Q is at the end of the wrench at (0.25,0,0) , where the forces are applied.
- (a) Describe the direction of the positive z-axis, given the axes shown in the figure.
- (b) Find the torque about P due to each of the three forces shown in the figure. Assume that the magnitude of each force is 250 N and the wrench is 0.25 m long.
- (c) Which force would be the most effective at causing the wrench to rotate as much as possible?

- (a) Answers will vary.
- (b) \tau_{1}=\dfrac{125}{2}\mathbf{k}\;\mathrm{Nm}; \tau_{2}=\dfrac{125\sqrt{2}}{4}\mathbf{k}\;\mathrm{Nm}; \tau_{3}=0\;\mathrm{Nm}
- (c) Answers will vary.
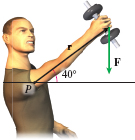
Exercise Science Suppose a person lifting a weight, extends his arm upward at 40^\circ above the horizontal while holding a 75- \text{N} (about 17-~\text{lb}) weight in his hand. His arm is 65 ~\text{cm} long from the shoulder socket to the weight. What is the magnitude of the torque?
732
Lorentz Force The Lorentz force on an electric charge moving through electric and magnetic fields is given by the formula \ \mathbf{F}=q\left[ \mathbf{E}+\left( \mathbf{v}\times \mathbf{B}\right) \right] . When the charge is expressed in coulombs ( \text{C}), the electric field in newtons per coulomb ( \text{N}/ \text{C}), the magnetic field in teslas ( \text{T}), and the velocity in meters per second (m/s), then the unit of force is newtons ( \text{N}). A positive charge (q=2.5~ \text{C}) is moving with velocity \mathbf{v}=\left( 0.0050\, \mathbf{i}+0.0035\,\mathbf{j}\right) \hbox{ m}/\hbox{s} through a region of space where there is an electric field \mathbf{E}=\left( 0.0064\,\mathbf{ i}-0.0075\,\mathbf{j}-0.0023\,\mathbf{k}\right) \text{N}/ \text{C} and a magnetic field \mathbf{B=} \left( 0.47\,\mathbf{i}+0.50\,\mathbf{j}-0.25\, \mathbf{k}\right) \text{T}. Find the Lorentz force acting on this charge.
0.0138125\mathbf{i}-0.015625\mathbf{j}-0.0036125\mathbf{k} N
Show that if \mathbf{u} and \mathbf{v} are orthogonal vectors, then \Vert \mathbf{u}\times \mathbf{v}\Vert =\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert .
Show that if \mathbf{u} and \mathbf{v} are orthogonal unit vectors, then \mathbf{u}\times \mathbf{v} is also a unit vector.
See Student Solutions Manual.
Algebraic Properties of the Cross Product Show that if \mathbf{v} and \mathbf{w} are vectors and a is a scalar, then a( \mathbf{v\times w}) =( a\mathbf{v}) \times \mathbf{w=v\times \,}( a\mathbf{w}) [property (3)].
Algebraic Properties of the Cross Product Show that if \mathbf{u}, \mathbf{v}, and \mathbf{w} are vectors, then \mathbf{ v}\times \left( \mathbf{w+u}\right) =\left( \mathbf{v}\times \mathbf{w} \right) +\left( \mathbf{v\times \,u}\right) [property (4)].
See Student Solutions Manual.
Algebraic Properties of the Cross Product Give an example to show that the cross product is not associative. That is, find vectors \mathbf{u}, \mathbf{v}, and \mathbf{w} so that \mathbf{u}\times ( \mathbf{v}\times \mathbf{w})\neq (\mathbf{u}\times \mathbf{v})\times \mathbf{ w}.
Algebraic Properties of the Cross Product If \mathbf{v} \times \mathbf{w}=\mathbf{0} and \mathbf{v}\,{ \cdot}\, \mathbf{w}=0, can you draw any conclusions about \mathbf{v} and/or \mathbf{w}? Explain.
Answers will vary.
Triple Scalar Product Problems 60-67 require the following definition. If \mathbf{u}, \mathbf{v}, and \mathbf{w} are three vectors in space, then \mathbf{u \,{ \cdot}\, ( \mathbf{v\times w})=\left\Vert \mathbf{u}\right\Vert \left\Vert \mathbf{v\times w}\right\Vert \cos \theta}, where \theta is the angle between \mathbf{u} and \mathbf{v \times w}, is called the triple scalar product of \mathbf{u}, \mathbf{v}, and \mathbf{w}.
In Problems 60 and 61, use the vectors \mathbf{u} = 2 \mathbf{i}+3 \mathbf{j}-4 \mathbf{k}, \mathbf{v} =-3 \mathbf{i}+ {\bf j}-4 \mathbf{k}, and \mathbf{w} = \mathbf{i}+ {\bf j} -3 \mathbf{k} to find each triple scalar product.
\mathbf{u}\,{ \cdot}\, ( \mathbf{v\times w})
( \mathbf{w\times u}) \,{ \cdot}\, \mathbf{v}
-21
Show that \mathbf{u}\,{ \cdot}\, (\mathbf{v}\times \mathbf{w})=( \mathbf{u}\times \mathbf{v})\,{ \cdot}\, \mathbf{w}.
Show that \mathbf{u}\,{ \cdot}\, (\mathbf{v}\times \mathbf{w})= \mathbf{v}\,{ \cdot}\, (\mathbf{w}\times \mathbf{u})=\mathbf{w}\,{ \cdot}\, (\mathbf{u} \times \mathbf{v}).
See Student Solutions Manual.
Show that three nonzero vectors \mathbf{u}, \mathbf{v}, and \mathbf{w} lie in the same plane if and only if \mathbf{u}\,{ \cdot}\, (\mathbf{v }\times \mathbf{w})=0.
If \mathbf{v}, \mathbf{w}, \mathbf{u} and \mathbf{v} ^{\prime }, \mathbf{w}^{\prime }, \mathbf{u}^{\prime } are vectors for which the following identities hold, \begin{eqnarray*} \mathbf{v}^{\prime }\,{ \cdot}\, \mathbf{v}&=&\mathbf{w}^{\prime }\,{ \cdot}\, \mathbf{w}= \mathbf{u}^{\prime }\,{ \cdot}\, \mathbf{u}=1\\ \mathbf{v}^{\prime }\,{ \cdot}\, \mathbf{w} &=& \mathbf{v}^{\prime }\,{ \cdot}\, \mathbf{u}=\mathbf{w}^{\prime }\,{ \cdot}\, \mathbf{v}=\mathbf{w}^{\prime }\,{ \cdot}\, \mathbf{u} =\mathbf{u}^{\prime }\,{ \cdot}\, \mathbf{v}=\mathbf{u}^{\prime }\,{ \cdot}\, \mathbf{w}=0 \end{eqnarray*}
show that \mathbf{v}^{\prime }=\frac{\mathbf{w}\times \mathbf{u}}{\mathbf{v}\,{ \cdot}\, \left( \mathbf{w}\times \mathbf{u}\right) }\qquad \mathbf{w}^{\prime }= \frac{\mathbf{u}\times \mathbf{v}}{\mathbf{v}\,{ \cdot}\, \left( \mathbf{w}\times \mathbf{u}\right) }\qquad \mathbf{u}^{\prime }=\frac{\mathbf{v}\times \mathbf{w}}{\mathbf{v}\,{ \cdot}\, \left( \mathbf{w}\times \mathbf{u}\right) }
See Student Solutions Manual.
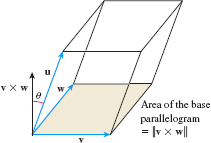
Volume of a Parallelepiped In Problems 66 and 67, find the volume of the parallelepiped whose adjacent sides are the given vectors. The volume V of a parallelepiped whose adjacent sides are the vectors \mathbf{u}, \mathbf{v}, and \mathbf{w} is V=|\mathbf{u\,{ \cdot}\, (\mathbf{v\times w})}|. See the figure. (You are asked to prove this in Problem 76.)
\mathbf{u=\,}2\mathbf{i}+\mathbf{j}-2\mathbf{k}, \mathbf{ v}=3\mathbf{i}-2\mathbf{j}+4\mathbf{k}, and \mathbf{w}=3\mathbf{i}+6 \mathbf{j}-2\mathbf{k}
\mathbf{u=\,}8\mathbf{i}-6\mathbf{j}+5\mathbf{k}, \mathbf{v}=2\mathbf{i}+3\mathbf{j}-8\mathbf{k}, and \mathbf{w}=\mathbf{i}+6 \mathbf{k}
249
Triple Vector Product Problems 68 and 69 use the following definition. If \mathbf{u}, \mathbf{v}, and \mathbf{w} are three vectors, the expression \mathbf{u}\times (\mathbf{v}\times \mathbf{w}) is called the triple vector product.
Show that \mathbf{u}\times (\mathbf{v}\times \mathbf{w})=( \mathbf{u}\,{ \cdot}\, \mathbf{w})\mathbf{v}-(\mathbf{u}\,{ \cdot}\, \mathbf{v})\mathbf{w}.
Show that \ \mathbf{u}\times (\mathbf{v}\times \mathbf{w})+ \mathbf{v}\times (\mathbf{w}\times \mathbf{u})+\mathbf{w}\times (\mathbf{u} \times \mathbf{v})=\mathbf{0}.
See Student Solutions Manual.
Prove Lagrange’s identity: (\mathbf{a}\times \mathbf{b})\,{ \cdot}\, (\mathbf{c}\times \mathbf{d})=(\mathbf{a}\,{ \cdot}\, \mathbf{c})( \mathbf{b}\,{ \cdot}\, \mathbf{d})-(\mathbf{a}\,{ \cdot}\, \mathbf{d})(\mathbf{b}\,{ \cdot}\, \mathbf{c}).
Prove that (\mathbf{a}\times \mathbf{b})\times (\mathbf{c} \times \mathbf{d})=[\mathbf{a}\,{ \cdot}\, (\mathbf{b}\times \mathbf{d})]\mathbf{c} -[\mathbf{a}\,{ \cdot}\, (\mathbf{b}\times \mathbf{c})]\mathbf{d}.
See Student Solutions Manual.
Geometry Proofs In Problems 72 and 73, use vector methods to prove each statement.
The diagonals of a parallelogram are perpendicular if and only if the parallelogram is a rhombus.
The altitudes of a triangle meet at one point; the medians of a triangle meet at one point.
See Student Solutions Manual.
Solve for \mathbf{x} in terms of a, \mathbf{a}, and \mathbf{b} if a\mathbf{x}+\mathbf{x}\times \mathbf{a}=\mathbf{b}, \ a\neq 0. (Hint: First find \mathbf{x}\,{ \cdot}\, \mathbf{a}, then \mathbf{x}\times \mathbf{a}.)
Challenge Problems
Prove that if \mathbf{u}=u_{1}\mathbf{i}+u_{2}\mathbf{j} +u_{3}\mathbf{k}, \mathbf{v}=v_{1}\mathbf{i}+v_{2}\mathbf{j}+v_{3} \mathbf{k}, and \mathbf{w}=w_{1}\mathbf{i}+w_{2}\mathbf{j}+w_{3}\mathbf{k} are three vectors, the triple scalar product \mathbf{u}\,{ \cdot}\, ( \mathbf{v}\times \mathbf{w}) is given by \mathbf{u}\,{ \cdot}\, (\mathbf{v}\times \mathbf{w})=\left\vert \begin{array}{l@{\quad}l@{\quad}l} u_{1} & u_{2} & u_{3} \\[3pt] v_{1} & v_{2} & v_{3} \\[3pt] w_{1} & w_{2} & w_{3} \end{array} \right\vert
See Student Solutions Manual.
Show that the volume V of a parallelepiped whose adjacent sides are the vectors \mathbf{u}, \mathbf{v}, and \mathbf{w} is V=| \mathbf{u}\,{ \cdot}\, (\mathbf{v}\times \mathbf{w})|.
The points A, B, and C determine a plane. If \mathbf{u}= \overrightarrow{\it OA}, \mathbf{v}=\overrightarrow{\it OB}, and \mathbf{w}= \overrightarrow{\it OC}, show that the vector \mathbf{u}\times \mathbf{v}+ \mathbf{v}\times \mathbf{w}+\mathbf{w}\times \mathbf{u} is normal to the plane.
See Student Solutions Manual.
Show that the volume of the tetrahedron with adjacent edges \mathbf{u}, \mathbf{v}, and \mathbf{w} is \dfrac{1}{6}\,\left\vert \, \mathbf{u}\,{ \cdot}\, (\mathbf{v}\times \mathbf{w})\right\vert .
Magnetic Force on a Charge When a charge q moves with velocity \mathbf{v} in a magnetic field \mathbf{B}, the field exerts a force \mathbf{F} on the charge that is perpendicular to both \mathbf{v} and \mathbf{B}, represented mathematically by \mathbf{F}_{ \hbox{mag}} = q\mathbf{v\times B}. In SI units, the charge q is measured in coulombs (\text{C}), the velocity \mathbf{v} is in meters per second (m/s), the force \mathbf{F} is in newtons ( \text{N}), and the magnetic field \mathbf{B} is in teslas ( \text{T}). Suppose a proton with a charge of q=1.60\times 10^{-19} \text{C} enters a magnetic field of 1.20 \text{T} that is pointing vertically downward and, as a result, experiences a horizontal force of 1.63\times 10^{-13} \text{N} to the left.
- (a) What are the magnitude and direction of the minimum velocity \mathbf{v} the charge could have had as it entered the field?
- (b) Why is the velocity in part (a) the minimum velocity?
- (a) ||\mathbf{v}||=8.49\times 10^5 m/s; The velocity v is parallel to -k.
- (b) Answers will vary.
733
Magnetic Effect on a TV In older analog televisions, the image on the screen was formed by a beam of electrons with charge q hitting the screen and causing it to glow. In some cases, the electrons reach speeds of v=2.0\times 10^{6}\ \text{m}/ \text{s}. Earth produces a magnetic field \mathbf{B} that exerts a magnetic force \mathbf{ F}_{\rm{mag}} on the moving electrons. The force \mathbf{F}_{\rm{mag}} is given by \mathbf{F}_{\rm{mag}}=q\mathbf{v}\times \mathbf{B}. Earth’s magnetic field is about 5.0\times 10^{-3} \text{T} and generally points horizontally from south to north. If the charge on an electron is q=1.60\times 10^{-19} \text{C}, find the magnitude and direction of the magnetic force \mathbf{F}_{\rm{mag}} on the electrons in a TV if the set is oriented so that the electrons move
- (a) from north to south.
- (b) from west to east.
Magnetic Force on an Extension Cord If a straight wire of length L carrying an electric current I is in a magnetic field \mathbf{B }, there will be a magnetic force \mathbf{F}_{\rm{mag}} on the wire. The magnetic force \mathbf{F}_{\rm{mag}} is orthogonal to both the wire and the field \mathbf{B}, and is given by \mathbf{F}_{\rm{mag}} =I\mathbf{L}\times \mathbf{B}, where the direction of the vector \mathbf{L} is the direction in which the current is flowing and its magnitude is L. An extension cord 2 \text{m} long carries a typical current I=5.0 amperes (A) and lies in a horizontal plane. Earth’s magnetic field \mathbf{B} has a magnitude of 5.0\times 10^{-3}~ \text{T} and points horizontally from south to north. The magnetic force \mathbf{F}_{\rm{mag} } is in newtons.
- (a) What is the minimum force Earth’s magnetic field can exert on the cord, and how should the cord be oriented relative to the field?
- (b) What is the maximum magnetic force Earth’s magnetic field will exert on the cord, and how should the cord be oriented relative to the field?
- (c) At what angle \theta relative to the magnetic field \mathbf{B} should the cord be oriented so that the magnetic force \mathbf{F}_\rm{mag} is 50% of its maximum possible value?
- (a) 0 N, south to north
- (b) 0.05 N, east to west
- (c) 30^\circ
