10.7 Assess Your UnderstandingPrinted Page 751
Concepts and Vocabulary
Multiple Choice The trace in the xy-plane of the graph of the equation x22−y23+z24=1 is [(a) x22+z24=1, (b) x22−y23=0, (c) x22−y23=1].
(c)
The intercept(s) of the graph of x24−y29−z=4 is(are) ________.
(1,0,0),(−1,0,0),(0,0,−4)
True or False A cylinder is formed when a line moves along a plane curve while remaining perpendicular to the plane containing the curve.
True
Multiple Choice The quadric surface z2=x2+y24 is called a(n) [(a) elliptic cylinder, (b) elliptic cone, (c) elliptic paraboloid, (d) hyperboloid].
(b)
The quadric surface y2−x2=4 is called a(n) ________.
Hyperbolic cylinder
The point (0,0,0) on the hyperbolic paraboloid z=y222−x252 is called a(n) ________ ________.
Saddle point
Skill Building
In Problems 7–18:
- (a) Identify the equation of each quadric surface.
- (b) List the intercepts and traces.
- (c)
 Graph each quadric surface.
Graph each quadric surface.
z=x2+y2
- (a) Elliptic paraboloid
- (b) Intercept: (0,0,0); traces: (0,0,0) in the xy-plane, z=x2 in the xz-plane, z=y2 in the yz-plane
- (c)
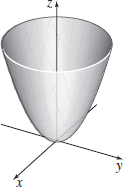
z=x2−y2
4x2+y2+4z2=4
- (a) Ellipsoid
- (b) Intercepts: (1,0,0),(−1,0,0),(0,2,0),(0,−2,0),(0,0,1) and (0,0,−1); traces 4x2+y2+4 in the xy-plane, x2+z2=1 in the xz-plane, y2+4z2=4 in the yz-plane
- (c)
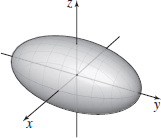
2x2+y2+z2=1
z2=x2+2y2
- (a) Elliptic cone
- (b) Intercept: (0,0,0); traces (0,0,0) in the xy-plane, z=±x in the xz-plane, z=±√2y in the yz-plane.
- (c)
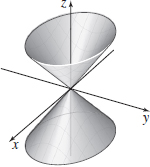
x2+2y2−z2=1
x=4z2
- (a) Parabolic cylinder
- (b) Traces x=4z2 in the xz-plane, x=0 in the xy-plane, z=0 in the yz-plane
- (c)
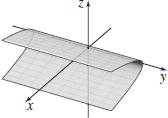
x2+y2=1
x2+2y2−z2=−4
- (a) Hyperboloid of two sheets
- (b) Intercepts: (0,0,2) and (0,0,−2); traces: ellipses defined for |z|>2 parallel to the xy-plane, z24−y22=1 in the yz-plane, z24−x24=1 in the xz-plane
- (c)
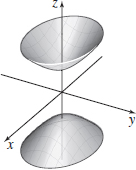
y2−x2=4
2x=y2
- (a) Parabolic cylinder
- (b) Intercepts: z=0; trace 2x=y2 in the xy-plane
- (c)
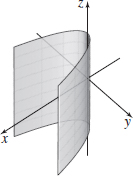
4y2−x2=1
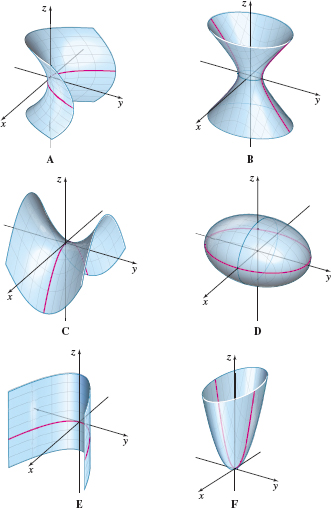
In Problems 19–24, use the Figures A-F to match each graph to an equation.
z=4y2−x2
C
2z=x2+4y2
2x2+y2−z2=1
B
2x2+y2+3z2=1
y2=4x
E
x2−z2=y
752
Figures G–L are graphs of quadric surfaces. In Problems 25–30, match each equation with its graph.
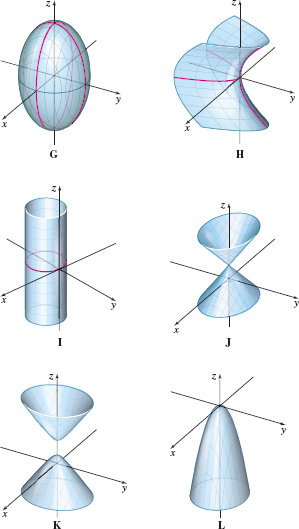
3x2+4y2+z=0
L
3x2+4y2+4y=0
3x2+2y2−(z−2)2+1=0
K
z2−4x2=3y
x2+2y2−z2+4z=4
J
3x2+3y2+z2=1
Applications and Extensions
Explain why the graph of xy=1 in space is a cylinder.
Answers will vary.
Explain why the graph of z=siny in space is a cylinder.
 Graph:
Graph:- (a) xy=1
- (b) z=siny
- (c) z=xy. (This surface is a hyperbolic paraboloid rotated 45∘ about the z-axis.)
- (a)
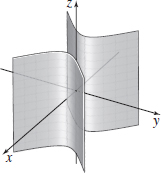
- (b)
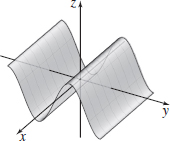
- (c)
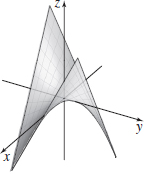
Challenge Problem
Show that through each point on the hyperboloid of one sheet x2a2+y2b2−z2c2=1
there are two lines lying entirely on the surface. (Hint: Write the equation as x2a2−z2c2=1−y2b2 and factor.)
