Vectors; Lines, Planes, and Quadric Surfaces in Space

10.1 Assess Your Understanding
Printed Page 698

Concepts and Vocabulary

True or False Each point in space is denoted by an ordered triple of real numbers.

True

True or False The point $( 0,4,0)$ lies on the $z$ -axis.

False

True or False The right-hand rule states that if your index finger points toward the positive $x$ -axis, and your other fingers point toward the positive $y$ -axis, then your thumb points toward the positive $z$ -axis.

True

True or False In space, the equation $y=3$ describes a plane.

True

In space, the set of all points a fixed distance $R$ from a fixed point $( x_{0},\,y_{0},\,z_{0})$ is called a(n) ______.

Sphere

The equation $x^{2}+y^{2}+z^{2}=8$ describes a sphere whose center is at the point ______.

$(0,0,0)$

Skill Building

In Problems 7–12, plot each point in space.

$(1, 1 ,1)$

$(1,1,1)$

$(0, 0 ,1)$

$(0, 2 ,5)$

$(0,2,5)$

$(-1, 0 ,5)$

$(-3,1,0)$

$(-3,1,0)$

$(4,-1,-3)$

698

In Problems 13–18, opposite vertices of a rectangular box whose edges are parallel to the coordinate axes are given. List the coordinates of the other six vertices of the box.

$(0,0,0);~(2,1,3)$

$(2,0,0)$ , $(0,1,0)$ , $(0,0,3)$ , $(2,1,0)$ , $(2,0,3)$ , $(0,1,3)$

$(0,0,0);~(4,2,2)$

$(1,2,3);~(3,4,5)$

$(1,4,3)$ , $(3,4,3)$ , $(3,2,3)$ , $(1,2,5)$ , $(1,4,5)$ , $(3,2,5)$

$(5,6,1);~(3,8,2)$

$(-1,0,2);~(4,2,5)$

$(-1,0,5)$ , $(4,2,2)$ , $(-1,2,2)$ , $(4,0,5)$ , $(4,0,2)$ , $(-1,2,5)$

$(-2,-3,0);~(-6,7,1)$

In Problems 19–28, describe in words the set of all points $(x,y,z)$ that satisfy the given statements.

$y=-2$

A plane parallel to the xz plane passing through the point ( $0, -2, 0$ )

$z=-3$

$x=0$

A plane in space, also known as the $yz$ -plane

$z=5$

$x=1$ and $y=0$

A line parallel to the $z$ -axis through the point ( $1, 0, 0$ )

$x=y$ and $z=0$

$x > -2$

The region of space where $x>-2$ and the $y$ and $z$ values are any real numbers

$0\leq y\leq 4$

$x^{2}+y^{2}+z^{2}\leq 1$

All points whose distance from the origin is at most 1.

$x^{2}+y^{2}+ z^{2} \geq 25$

In Problems 29–34, find the distance between each pair of points.

$(3,2,5)$ and $(-1,2,2)$

$5$

$(12,-5,16)$ and $(21,15,4)$

$(-1,2,-3)$ and $(4,-2,1)$

$\sqrt{57}$

$(1.0,3.2,4.5)$ and $(1.4,1.0,6.5)$

$(4,-2,-2)$ and $(3,2,1)$

$\sqrt{26}$

$(2,-3,-3)$ and $(4,1,-1)$

In Problems 35–38, find the equation of a sphere with radius $R$ and center at $P_{0}$ .

$R=1$ ; $P_{0}=(3,1,1)$

$(x-3)^2+(y-1)^2+(z-1)^2=1$

$R=2$ ; $P_{0}=(1,2,2)$

$R=3$ ; $P_{0}=(-1,1,2)$

$(x+1)^2+(y-1)^2+(z-2)^2=9$

$R=1$ ; $P_{0}=(-3,1,-1)$

In Problems 39–44, find the radius and center of each sphere.

$x^{2}+y^{2}+z^{2}+2x-2y=2$

Radius $2$ ; center $(-1,1,0)$

$x^{2}+y^{2}+z^{2}+2x-2z=-1$

$x^{2}+y^{2}+z^{2}+4x-4y+2z=0$

Radius $3$ ; center $(-2,2,-1)$

$x^{2}+y^{2}+z^{2}-4x=0$

$2x^{2}+2y^{2}+2z^{2}-8x+5z+1=0$

Radius $\dfrac{9}{4}$ ; center $\left(2,0,-\dfrac{5}{4}\right)$

$3x^{2}+3y^{2}+3z^{2}+6x-y-3=0$

Applications and Extensions

In Problems 45–50, write the equation of each sphere.

The endpoints of a diameter are $(-2, 0, 4)$ and $(2, 6, 8)$ .

$x^2+(y-3)^2+(z-6)^2=17$

The endpoints of a diameter are $(1, 3, 6)$ and $(-3, 1, 4)$ .

The center is at $(-3, 2, 1)$ , and the sphere passes through the point $(4,-1, 3)$ .

$(x+3)^2+(y-2)^2+(z-1)^2=62$

The center is at $(0,-3, 4)$ , and the sphere passes through the point $(2, 1, 1)$ .

The center is at $( 2,1,-2)$ and the sphere is tangent to the $xy$ -plane.

$(x-2)^2+(y-1)^2+(z+2)^2=4$

The center is at $( 1,5,4)$ and the sphere is tangent to the $yz$ -plane.

Chemistry: Iron Crystals In its solid form, iron forms a crystal lattice known as a body-centered cubic (bcc). This crystal consists of eight iron atoms at the corners of a cube plus one more atom at the center of the cube. The sides of the cube are 0.287nm long (1nm = 10^-9m). Put one corner of the cube at the origin, and place three of the faces along the positive coordinate planes.
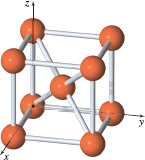
1. (a) Assign coordinates to each atom in the crystal.
2. (b) What are the coordinates of the atom that is furthest from the origin?
3. (c) What are the coordinates of the atom at the center of the cube?
4. Find the distance between the iron atom at the center of the cube and the atom in the $xz$ -plane that is farthest from the origin.

$(0,0,0)$ , $(0.287,0,0)$ , $(0.287,0.287,0)$ , $(0,0.287,0)$ , $(0,0,0.287)$ , $(0.287,0,0.287)$ , $(0, 0.287, 0.287)$ , $(0.287,0.287,0.287)$ , $(0.1435,0.1435,0.1435)$
$(0.287,0.287,0.287)$
$(0.1435,0.1435,0.1435)$
$\approx \!0.249$

Equilateral Triangle Show that the points $(2,4,2)$ , (2,1,5) and $(5,1,2)$ are the vertices of an equilateral triangle.

Sphere
1. Find an equation of the sphere with center at $( 4,0,-2)$ and radius 5.
2. Describe the intersection of the sphere and the $xy$ -plane.

Answers will vary.

Right Triangle Inscribed in a Sphere
1. Show that the points $(-2,6,0)$ , $(4,9,1)$ , and $(-3,2,18)$ are the vertices of a right triangle.
2. (b) Find an equation of the sphere that passes through the vertices of the right triangle and that has a diameter along its hypotenuse.

Distance Find the shortest distance from the point $(4, 2, -1)$ to the $xy$ -plane.

$1$

Midpoint Formula Derive a formula to find the midpoint of the line segment joining two points in space.

Challenge Problems

Sphere Find an equation of the sphere passing through $(3,0,0)$ , $(0,0,1)$ , $(-1,-3, 1)$ , and $(2,0,1)$ .

$(x-1)^2+(y+2)^2+(z+1)^2=9$

Sphere
1. Show that the graph of $\begin{equation*} Ax^{2}+Ay^{2}+Az^{2}+Dx+Ey+Fz=G, \qquad A\gt 0 \end{equation*}$ is a sphere, a point, or the empty set.
2. (b) When is it a sphere? What are its center and radius?

10.1 Assess Your UnderstandingPrinted Page 698

10.1 Assess Your Understanding
Printed Page 698