10.2 Assess Your UnderstandingPrinted Page 702
Concepts and Vocabulary
True or False A vector is an object that has magnitude and direction.
True
Scalars are quantities that have only ______.
Magnitude
The product of a scalar a and a vector v is called a(n) _____ ______ of v.
Scalar multiple
Multiple Choice The vectors −v and v have [(a) the same, (b) different] magnitude and the [(c) same, (d) opposite] direction.
(a); (d)
Skill Building
State which of the following are scalars and which are vectors:
- (a) Volume
- (b) Speed
- (c) Force
- (d) Work
- (e) Mass
- (f) Distance
- (g) Age
- (h) Velocity
Scalars: (a), (b), (d), (e), (f), (g). Vectors: (c), (h)
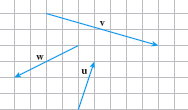
In Problems 6–14, use the vectors in the above figure to graph each of the following vectors:
2v
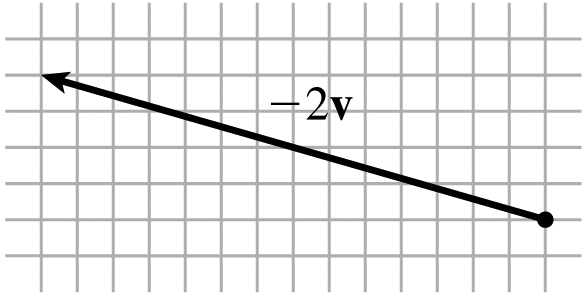
−2v
v+w
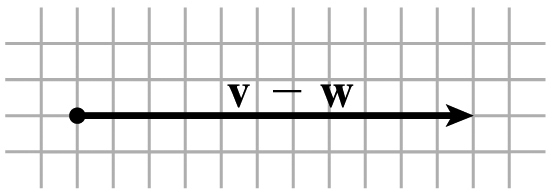
v−w
w−v
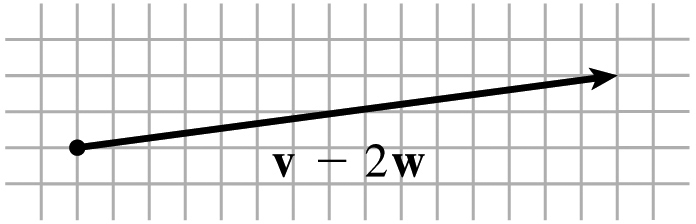
v−2w
(v+w)+3u
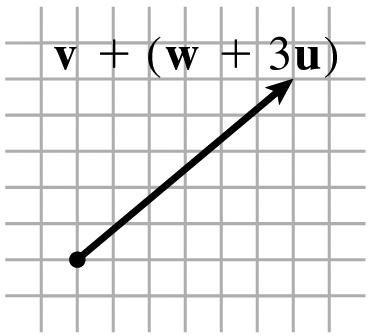
v+(w+3u)
2u−13(v−w)
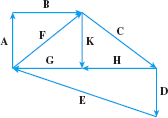
In Problems 15–22, use the vectors in the figure below.
Find the vector x if x+B=F.
x=A
Find the vector x if x+K=C.
703
Write C in terms of E , D , and F.
C=−D−E−F
Write G in terms of C , D , E, and K.
Write E in terms of G , H , and D.
E=G+H−D
Write E in terms of A , B , C , and D.
What is A+B+K+G?
0
What is A+B+C+H+G?
Applications and Extensions
Resultant Force Two forces F1 and F2 act on an object shown in the figure. Graph the vector representing the resultant force; that is, find F1+F2.

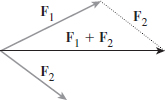
Resultant Force Two forces F1 and F2 act on an object shown in the figure. Graph the vector representing the resultant force; that is, find F1+F2.
Air Travel An airplane is flying due north at a constant airspeed of 560 mi/h. There is a wind 75mi/h blowing from the east.
- (a) Draw vectors representing the velocities of the airplane and the wind.
- (b) Draw the vector representing the airplane’s ground speed.
- (c) Interpret the result.
- (a)
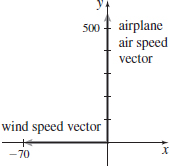
- (b)
- (c) Answers will vary.
Air Travel An airplane maintains a constant airspeed of 500km/h headed due west. There is a tail wind blowing at 500km/h.
- (a) Draw vectors representing the velocities of the airplane and the tail wind.
- (b) Draw the vector representing the airplane’s ground speed.
- (c) Interpret the result.
Suppose v and w are nonzero vectors represented by arrows with the same initial point, and that the terminal points of v and w are P and Q, respectively. Suppose the vector u is represented by an arrow from the initial point of v to the midpoint of the directed line segment →PQ. Write u in terms of v and w.
u=12(v+w)
Find nonzero scalars a and b so that 4v+a(v−w)+b(v+w)=0
for every pair of vectors v and w.
