REVIEW EXERCISESPrinted Page 9999
In Problems 1–4, for each vector function r=r(t)
- (a) Find the domain.
- (b) Graph the curve C traced out by r=r(t), indicating its orientation.
- (c) Find the value of r′(t) at the given number t.
r(t)=t2i+3tj,t=2
- (a) All real numbers.
- (b)
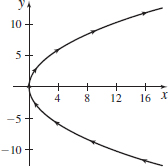
- (c) r′(2)=4i+3j
r(t)=3costi+sintj,0≤t≤π,t=π3
r(t)=ti+2costj+2sintk,t=0
- (a) All real numbers.
- (b)
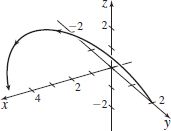
- (c) r′(0)=i+2k
r(t)=ti+tj−2k,t=1
Find lim.
\dfrac12 \mathbf{j} -\dfrac43 \mathbf{k}
In Problems 6 and 7, determine if the vector function is continuous at each number in the given interval. Identify any numbers where \mathbf{r} =\mathbf{r}(t) is discontinuous.
\mathbf{r}( t)\;=\;\dfrac{t}{t-2}\mathbf{i}+\sin t \mathbf{j}, interval ( 0,2\pi )
\mathbf{r}( t)\;=\;\dfrac{t}{t+1}\mathbf{i}+\sqrt{t-1}\mathbf{j}+3t \mathbf{k}, interval [ 1,3]
Continuous
In Problems 8 and 9, find {\bf r}^{\prime} (t) and {\bf r}^{\prime \prime} (t).
\mathbf{r}(t)=3t\mathbf{i}-\ln t\mathbf{j}+2e^{t}\mathbf{k}
\mathbf{r}(t)=2\cos t\mathbf{i}+3\cos t\mathbf{j}+t\mathbf{k}
\mathbf{r}\,' (t) = -2\sin t \mathbf{i} -3 \sin t \mathbf{j} +\mathbf{k} and \mathbf{r}\,''(t) = -2 \cos t \mathbf{i} - 3 \cos t \mathbf{j}
In Problems 10 and 11, find [{\bf f}(t)\,{\cdot}\, {\bf g} (t)]^{\prime} and [{\bf f}(t)\times {\bf g}(t)]^{\prime} .
\mathbf{f}(t)=t\mathbf{i}-\dfrac{t}{2}\mathbf{j}+\mathbf{k} and \mathbf{g}(t)=\sqrt{1-t}\mathbf{i}+t^{3}\mathbf{j}+2( t+1) \mathbf{k}
\mathbf{f}(t)=t\mathbf{i}+\cos ( 2t) \mathbf{j} -5 \mathbf{k} and \mathbf{g}(t)=2t\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k}
[\mathbf{f}(t) \cdot \mathbf{g}(t)]' = 4t - 2\sin (2t) \cos t - \cos(2t) \sin t - 5\cos t and [\mathbf{f}(t) \times \mathbf{g}(t)]' = (-2\sin(2t) \sin t + \cos (2t) \cos t - 5 \sin t) \mathbf{i} + (-10 - \sin t - t \cos t) \mathbf{j} + (\cos t - t \sin t + 4t \sin (2t) - 2\cos(2t)) \mathbf{k}
In Problems 12–14, for each curve C traced out by \mathbf{r}=\mathbf{r} ( t) :
- (a) Find a tangent vector to each curve C at t=0.
- (b) Find the unit tangent vector \mathbf{T} at t=0
- (c) Find the principal unit normal vector \mathbf{N} at t=0
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\mathbf{k}
\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+\sqrt{1-5t^{2}} \mathbf{k}, \dfrac{-\sqrt{5}}{5}< t< \dfrac{\sqrt{5}}{5}
- (a) \mathbf{r}\, '(0) = \mathbf{i}+2\mathbf{j}
- (b) \mathbf{T}(0) = \dfrac{\sqrt{5}}{5}\mathbf{i} + \dfrac{2\sqrt{5}}{5} \mathbf{j}
- (c) \mathbf{N}(0) = -\mathbf{k}
\mathbf{r}(t)=e^{t}\sin t\mathbf{i}+e^{t}\cos t\mathbf{j}+e^{t}\mathbf{k}
Find the acute angle between the tangent vector to the helix traced out by \mathbf{r} ( t)\;=\;\sin t\mathbf{i}+3t\mathbf{j}+\cos t\mathbf{k} and the direction \mathbf{j}.
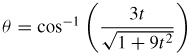
In Problems 16–18, find the arc length of each vector function.
\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j} from t=\;0 to t=2\pi
\mathbf{r}(t)=t\mathbf{i} +2t\mathbf{j}+\sqrt{1-5t^{2}}\mathbf{k} from t=0 to t=\dfrac{{1}}{4 }
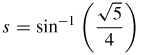
\mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+\dfrac{t}{5} \mathbf{k} from t=\;0 to t=2\pi
In Problems 19 and 20, determine whether the parameter is arc length.
\mathbf{r}(t)=3t\mathbf{i}+4t\mathbf{j}\; +\left( 5t+1\right) \mathbf{k}
No
\mathbf{r}(t)=3\cos t\mathbf{i}+3\sin t\mathbf{j}\;+8t\mathbf{k}
In Problems 21–23, find the curvature \kappa\;=\;\kappa (t) of the curve C traced out by each vector function {\bf r}={\bf r}( t) .
\mathbf{r}(t)=4\cos t\mathbf{i}-4\sin t\mathbf{j}
\dfrac14
\mathbf{r}(t)=t\mathbf{i}+\cos t \mathbf{j}\;+\sin t\mathbf{k}
\mathbf{r}(t)=e^{t}\mathbf{i}+4t\mathbf{j}\;+5e^{-t}\mathbf{k}
\kappa = \dfrac{2 \sqrt{4e^{2t} + 100 e^{-2t}+25}}{(e^{2t} + 25e^{-2t}+16)^{\frac32}}
Find the curvature of the graph of y=x^{3}-4 at the point ( 1,-3).
Find the curvature of the graph of y=4e^{-2x} at the point ( 0,4).
\kappa = \dfrac{16}{65^{3/2}}
In Problems 26–28, find the radius of the osculating circle at the point corresponding to t on the curve C traced out by each vector function.
\mathbf{r}(t)=( 1-t^{2}) \mathbf{i}+e^{-t}\mathbf{j, }\;t=0
\mathbf{r}(t)=\cos ^{2}t \mathbf{i}+\sin ^{2}t\mathbf{j},\;t=\dfrac{\pi }{3}
\rho = \infty
\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+\sqrt{1-t^{2}}\mathbf{k} ,\;-1< t< \;1,\;t=0
Find the curvature of the curve y=\sqrt[3]{x}, x>0.
\kappa = \dfrac{6x^{1/3}}{(9x^{4/3}+1)^{3/2}}
Find the minimum curvature of the curve C traced out by the vector function \mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}.
In Problems 31–34:
- (a) Find the velocity {v}, acceleration {a}, and speed v of a particle traveling along the curve traced out by the vector function \mathbf{r}= \mathbf{r}(t).
- (b) Find the tangential and normal components of the acceleration.
\mathbf{r}(t)=2\cos t\mathbf{i}+\sin t\mathbf{j}
- (a) \mathbf{v}(t) = -2\sin t \mathbf{i} + \cos t \mathbf{j}, \mathbf{a}(t) = -2\cos t \mathbf{i} - \sin t \mathbf{j}, and v(t) = \sqrt{3\sin^2 t + 1}
- (b) a_{\mathbf T} =\dfrac{3 \sin t \cos t}{\sqrt{3\sin ^2 t + 1}}, a_{\mathbf N} = \dfrac2{\sqrt{3\sin ^2 t + 1}}
\mathbf{r}(t)=e^{t}\sin t\mathbf{i} +e^{-t}\mathbf{j}
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\mathbf{k}
- (a) \mathbf{v}(t) = e^t \mathbf{i} - e^{-t} \mathbf{j}, \mathbf{a}(t) = e^t \mathbf{i} + e^{-t} \mathbf{j}, and v(t) = \sqrt{e^{2t}+e^{-2t}}
- (b) a_{\mathbf T} = \dfrac{e^{2t} - e^{-2t}}{\sqrt{e^{2t} + e^{-2t}}}, a_{\mathbf N} = \dfrac{2}{\sqrt{e^{2t} + e^{-2t}}}
\mathbf{r}(t)=e^{t}\sin t \mathbf{i}+e^{t}\cos t\mathbf{j}+e^{t}\mathbf{k}
Find the velocity and acceleration of a particle moving on the cycloid \mathbf{r}( t)\;=\;[ \pi t-\sin ( \pi t) ] \mathbf{i} +[ 1-\cos ( \pi t) ] \mathbf{j}.
\mathbf{v}(t) = (\pi - \cos(\pi t)) \mathbf{i} + \pi \sin (\pi t) \mathbf{j} and \mathbf{a}(t) = \pi^2 \sin (\pi t) \mathbf{i} + \pi^2 \cos (\pi t) \mathbf{j}
- (a) Find the velocity and acceleration of a particle moving on the parabola \mathbf{r}( t)\;=\;( t^{2}-2t)\kern.7pt\mathbf{i}+t~\mathbf{j}.
- (b) At what time t is the speed of the particle 0?
In Problems 37 and 38, find each integral.
\int [ ( t^{2}-2) \mathbf{i}-( t-2) ^{2}\mathbf{j}+e^{2t}\mathbf{k}] dt
\left(\dfrac13 t^3 - 2t\right) \mathbf{i} - \dfrac{(t-2)^3}3 \mathbf{j} + \dfrac12 e^{2t} \mathbf{k} + \mathbf{c}
\int \left(\cos \dfrac{t}{2}\mathbf{i}+\sin ^{2}\left( \dfrac{t}{2}\right) \mathbf{j}+3t\mathbf{k}\right)dt
In Problems 39–41, solve each vector differential equation with the given boundary condition.
\mathbf{r}^{\prime} ( t)\;=\;e^{2t}\mathbf{i}+\ln t \mathbf{j}+2e^{t}\mathbf{k,}\;\mathbf{r}(1)=\mathbf{j}+\mathbf{k}
\mathbf{r}(t) = \left( \dfrac12 e^{2t} - \dfrac12 e^2 \right) \mathbf{i} + (t \ln t - t + 2) \mathbf{j} + (2e^t - 2e + 1) \mathbf{k}
\mathbf{r}^{\prime} (t)=\sin t\cos t\mathbf{i}+\tan t\sec t \mathbf{j}+t\mathbf{k,}\;\mathbf{r}(0)=\mathbf{i}+\mathbf{k}
\dfrac{d\mathbf{r}}{dt}=\cos t\mathbf{i}-\sin t\mathbf{j} +\dfrac{t}{2}\mathbf{k,}\;\mathbf{r}( 0)\;=\;\mathbf{i}
\mathbf{r}(t) = (\sin t + 1) \mathbf{i} + (\cos t - 1) \mathbf{j} +\dfrac{t^2}4 \mathbf{k}
Find the speed, velocity, and position at time t for a particle whose acceleration at time t is given by \mathbf{a}(t)=\tan t\sec t\mathbf{i}+\cos {t}\mathbf{j}. Assume that the initial velocity and position are \mathbf{0}.
Projectile Motion A projectile is fired with a speed of 500{\textrm m}/\!{\textrm s} at an inclination of 45° %TCIMACRO{\U{b0}}% %BeginExpansion {{}^\circ}% %EndExpansion to the horizontal from a point 30{\textrm m} above level ground. Find the point where the projectile strikes the ground.
\approx \!25{,}540 m away
State Kepler's three laws of Planetary Motion. Explain each law in your own words.