11.1 Assess Your UnderstandingPrinted Page 765
765
Concepts and Vocabulary
The domain of r(t)=(4t+1)i+√4−tj+k is _______.
{t|t≤4}
True or False A vector function is continuous at a real number t0 if at least one of its component functions is continuous at t0.
False
True or False To find the derivative of a vector function r=r(t), find the derivative of each of its component functions.
True
True or False The derivative of a dot product is a scalar function.
True
True or False If y=f(t) is a differentiable real (scalar) function and r=r(t) is a differentiable vector function, then ddt[f(t)r(t)]=f′(t)ddtr(t).
False
If u=u(t) and v=v(t) are vector functions in space that are differentiable, then ddt(u×v)=______.
u′×v+u×v′
Skill Building
In Problems 7–14, find the value of each vector function at t.
r(t)=t2i−2tj at t=1
i−2j
r(t)=t3i+2tj at t=2
v(t)=sinti−costj at t=π4
√22i−√22j
v(t)=tanti+cos(2t)j at t=0
u(t)=e2ti+t2j−2k at t=0
i−2k
u(t)=lnti−j+t3k at t=1
g(t)=ti−cos(πt4)j+2tk at t=4
4i+j+8k
f(t)=sin(3πt4)i+3j−3t2k at t=1
In Problems 15–22, find the domain of each vector function.
r(t)=costi+sintj+2k
All real numbers
r(t)=cos(2t)i+sintj+2tk
f(t)=√ti+tj−k
{t|t≥0}
r(t)=t2i+1√tj−tk
u(t)=(t2+1)ti+3tj−2tk
{t|t≠0}
v(t)=eti+(5+3t)j−2tk
v(t)=lnti+(t+1)j+4tk
{t|t>0}
v(t)=√ti+lntj+tk
In Problems 23–36, graph the curve C traced out by each vector function and show its orientation.
r(t)=2ti+t2j,t≥0
r(t)=t2i−4tj,t≤0
r(t)=ti,−1≤t≤1
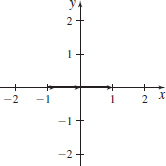
r(t)=tj,−1≤t≤1
r(t)=ti+tj
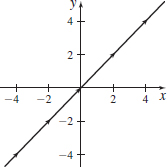
r(t)=3ti+2tj
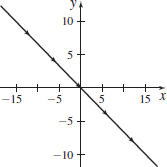
r(t)=3ti−2tj
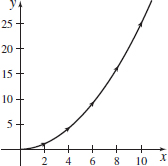
r(t)=ti+t2j
r(t)=costi−sintj,0≤t≤π2
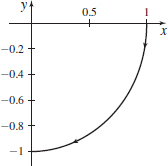
r(t)=costi+sintj,0≤t≤π2
r(t)=sin2ti+cos2tj,0≤t≤π2
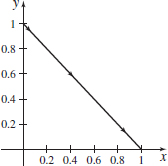
r(t)=sin2ti−cos2tj,0≤t≤π2
 r(t)=sinti+t2j,0≤t≤4π
r(t)=sinti+t2j,0≤t≤4π
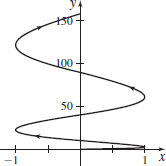
 r(t)=sin3ti+cos3tj,0≤t≤2π
r(t)=sin3ti+cos3tj,0≤t≤2π
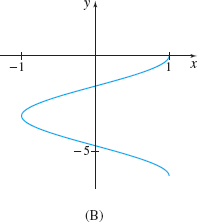
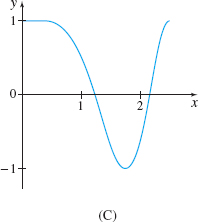
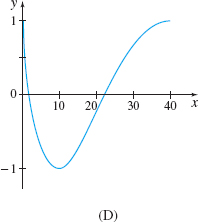
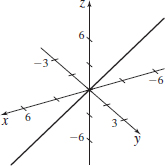
In Problems 37–40, match each vector function to its plane curve.
r(t)=t2i+costj,0≤t≤2π
D
r(t)=costi+t2j,0≤t≤2π
r(t)=√ti+costj,0≤t≤2π
C
r(t)=costi−tj,0≤t≤2π
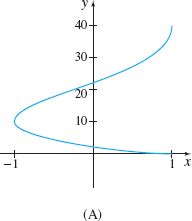
![]() In Problems 41–48, graph the curve C traced out by each vector function.
In Problems 41–48, graph the curve C traced out by each vector function.
r(t)=(2t+1)i+t3j−(t+1)k
r(t)=ti+tj−(t+1)k
r(t)=2costi+tj+2sintk,−2π≤t≤2π
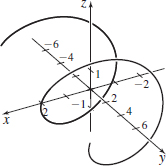
r(t)=t2i+3sintj+2costk,−2π≤t≤2π
r(t)=4costi+sintj+etk,−π≤t≤2π
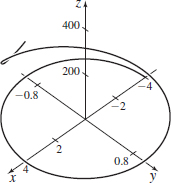
r(t)=ti+sintj+etk,−5≤t≤5
r(t)=3costi+3sintj+sin(2t)k,0≤t≤2π
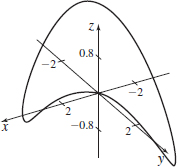
r(t)=ti+tcos(3t)j +tsin(3t)k,0≤t≤2π
In Problems 49–56, determine where each vector function is continuous.
r(t)=t2i+21−t2j+sintk
{t|t≠−1,1}
r(t)=lnti+e−tj
766
r(t)=secti−costj
{t|t≠(2k+1)π2}
r(t)=√t+1i+tantj−sint−1tk
r(t)=tt+1i−tj
{t|t≠−1}
r(t)=tt2+1i+tj
r(t)=sinti−tantj+k
{t|t≠(2k+1)π2}
r(t)=secti+csctj+k
In Problems 57–72, find r′(t) and r′′(t).
r(t)=4t2i−2t3j
r′(t)=8ti−6t2j and r″
\mathbf{r}(t)=8t\mathbf{i}+4t^{3}\mathbf{j}
\mathbf{r}(t)=4\sqrt{t}\kern.7pt\mathbf{i}+2e^{t}\mathbf{j}
\mathbf{r}\,'(t) = \dfrac{2\sqrt{t}}{t} \mathbf{i} + 2e^t \mathbf{j} and \mathbf{r}\,''(t) = - \dfrac{1}{t^{3/2}} \mathbf{i} + 2e^t \mathbf{j}
\mathbf{r}(t)=e^{3t}\mathbf{i}+\sqrt[3]{t}\mathbf{j}
\mathbf{r}(t)=\mathbf{i}+t\mathbf{j}+t^{2}\mathbf{k}
\mathbf{r}\,'(t) = \mathbf{j} + 2t \mathbf{k} and \mathbf{r}\,''(t) = 2\mathbf{k}
\mathbf{r}(t)=\mathbf{i}-\mathbf{j}+t\mathbf{k}
\mathbf{r}(t)=t^{2}\mathbf{i}+t^{3}\mathbf{j}-t\mathbf{k}
\mathbf{r}\,'(t) = 2t \mathbf{i} + 3t ^2 \mathbf{j} - \mathbf{k} and \mathbf{r}\,''(t) = 2 \mathbf{i} + 6t \mathbf{j}
\mathbf{r}(t)=(1+t)\mathbf{i}-3t^{2}\mathbf{j}+t\mathbf{k}
\mathbf{r}(t)=\sin ^{2}t\mathbf{i}-\cos ^{2}t\mathbf{j}
\mathbf{r}\,'(t) = \sin (2t) \mathbf{i} + \sin (2t) \mathbf{j} and \mathbf{r}\,''(t) = 2 \cos (2t) \mathbf{i} + 2 \cos (2t) \mathbf{j}
\mathbf{r}(t)=\sin ( 2t) \mathbf{i}-\cos (2t) \mathbf{j}
\mathbf{r}(t)=5e^{t^{2}+t}\mathbf{i}-\ln e^{t^{2}+t}\mathbf{j}
\mathbf{r}\,'(t) = 5e^{t^2+t}(2t+1) \mathbf{i}-(2t+1) \mathbf{j} and \mathbf{r}\,''(t) = 5e^{t^2+t}(4t^2+4t+3) \mathbf{i} - 2 \mathbf{j}
\mathbf{r}(t)= \sin (3t^{3}-t)\mathbf{i} -\cos ^{2}(3t^{3}-t)\mathbf{j}
\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+t\mathbf{k}
\mathbf{r}\,'(t) = (e^t \cos t - e^t \sin t) \mathbf{i} + (e^t \sin t + e^t \cos t) \mathbf{j} + \mathbf{k} and \mathbf{r}\,''(t) = -2e^t \sin t \mathbf{i} + 2e^t \cos t \mathbf{j}
\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-t\mathbf{k}
\mathbf{r}(t)=(t-t^{3})\mathbf{i}+(t+t^{3})\mathbf{j}-t\mathbf{k}
\mathbf{r}\,'(t) = (1-3t^2) \mathbf{i} + (1+3t^2)\mathbf{j} - \mathbf{k} and \mathbf{r}\,''(t) = -6t\mathbf{i} + 6t \mathbf{j}
\mathbf{r}(t)=(t^{2}-t)\mathbf{i}+(t^{2}+t)\mathbf{j}+t\mathbf{k}
In Problems 73–78, find \frac {d}{dt}\left[ \mathbf{u}(t)\,{\cdot}\, \mathbf{v}(t)\right].
\mathbf{u}(t)=t^{2}\mathbf{i}-t\mathbf{j} \quad and \quad \mathbf{v}(t)=t\mathbf{i}+t^{2}\mathbf{j}
\dfrac{d}{dt}[\mathbf{u}(t)\cdot\mathbf{v}(t)]=0
\mathbf{u}(t)=t^{3}\mathbf{i}+t\mathbf{j} \quad and \quad \mathbf{v}(t)=t\mathbf{i}-2t\mathbf{j}
\mathbf{u}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j} \quad and \quad \mathbf{v}(t)=t\mathbf{i}-t^{2}\mathbf{j}
\dfrac{d}{dt}[\mathbf{u}(t)\cdot\mathbf{v}(t)]= te^t+e^t+t^2e^{-t} - 2te^{-t}
\mathbf{u}(t)=t\mathbf{i}+4\sqrt{t}\mathbf{j} \quad and \quad \mathbf{v}(t)=2t\mathbf{i}-t^{2}\mathbf{j}
\mathbf{u}(t)=\sin ( \omega t) \mathbf{i}+\cos( \omega t) \mathbf{j} \quad and \quad \mathbf{v}(t)=\mathbf{i}+\mathbf{j}
\dfrac{d}{dt}[\mathbf{u}(t)\cdot\mathbf{v}(t)]= \omega \cos (\omega t) - \omega \sin (\omega t)
\mathbf{u}(t)=\sin ^{2}t\mathbf{i}-\cos^{2}t\mathbf{j} \quad and \quad \mathbf{v}(t)=\mathbf{i}-\mathbf{j}
In Problems 79–82, find \dfrac{d}{dt}[\mathbf{u}(t)\,{\cdot}\,\mathbf{v}(t)] and \dfrac{d}{dt}[\mathbf{u}(t)\times \mathbf{v}(t)].
\mathbf{u}(t)=2t\mathbf{i}+t^{2}\mathbf{j}-5\mathbf{k} \quad and \quad \mathbf{v}(t)=t^{2}\mathbf{i}+2t\mathbf{j}+\mathbf{k}
\dfrac{d}{dt}[\mathbf{u}(t)\cdot\mathbf{v}(t)]= 12t^2 and \dfrac{d}{dt}[\mathbf{u}(t)\times\mathbf{v}(t)]= (2t+10) \mathbf{i} -(10t+2) \mathbf{j} + (8t-4t^3) \mathbf{k}
\mathbf{u}(t)=t^{3}\mathbf{i}-t^{2}\mathbf{j}+t\mathbf{k} \quad and \quad \mathbf{v}(t)=t\mathbf{i}-t^{2}\mathbf{j}+t^{3}\mathbf{k}
\mathbf{u}(t)=\cos ( 2t) \mathbf{i}+\sin (2t) \mathbf{j}+\mathbf{k} \quad and \quad \mathbf{v}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+\mathbf{k}
\dfrac{d}{dt}[\mathbf{u}(t)\cdot\mathbf{v}(t)]=\sin t \cos(2t)-\sin(2t)\cos t and \dfrac{d}{dt}[\mathbf{u}(t)\times\mathbf{v}(t)]= (2\cos(2t)-\cos t) \mathbf{i} + (2 \sin(2t) - \sin t) \mathbf{j}-(\sin(2t)\sin t+\cos(2t)\cos t) \mathbf{k}
\mathbf{u}(t)=e^{2t}\mathbf{i}+e^{-2t}\mathbf{j}+t\mathbf{k} \quad and \quad \mathbf{v}(t)=e^{-t}\mathbf{i}+e^{-2t}\mathbf{j}-t\mathbf{k}
Applications and Extensions
Given the vector function \mathbf{u}(t) =\cos( \omega t) \mathbf{i}+\sin ( \omega t) \mathbf{j}, find \dfrac{d\mathbf{u}}{dt} and \left\Vert \dfrac{d\mathbf{u}}{dt}\right\Vert.
\dfrac{d\mathbf{u}}{dt} = -\omega \sin(\omega t) \mathbf{i} + \omega \cos(\omega t) \mathbf{j} and \left\| \dfrac{d\mathbf{u}}{dt} \right\|\;=\;|\omega|
Given the vector function \mathbf{v}(t) =t\mathbf{i}+t^{2}\mathbf{j}+t^{3}\mathbf{k}, find \dfrac{d^{2}\mathbf{v}}{dt^{2}} and \left\Vert \dfrac{d^{2}\mathbf{v}}{dt^{2}}\right\Vert.
For \mathbf{f}(t)=\sin t\mathbf{i}-\cos t\mathbf{j}, show that \mathbf{f}(t) and \mathbf{f}^{\,\prime \prime} (t) are parallel.
See Student Solutions Manual.
For \mathbf{f}(t)=e^{3t}\mathbf{i}+e^{-3t}\mathbf{j}, show that \mathbf{f}(t) and \mathbf{f}^{\,\prime \prime} (t) are parallel.
In Problems 87–94, a vector function \mathbf{r}=\mathbf{r}(t), defining a curve in the plane is given. Graph each curve, indicating its orientation. Include in the graph the vector \mathbf{r}(0) and \mathbf{r}^{\prime} (0). Draw \mathbf{r}^{\prime} (0) so its initial point is at the terminal point of \mathbf{r}(0).
\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}
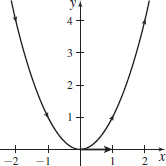
\mathbf{r}(t)=2t^{2}\mathbf{i}-t\mathbf{j}
\mathbf{r}(t)=t\mathbf{i}+e^{t}\mathbf{j}
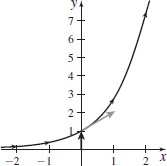
\mathbf{r}(t)=t\mathbf{i}+\ln (1+t)\mathbf{j}
\mathbf{r}(t)=3\sin t\mathbf{i}-3\cos t\mathbf{j}
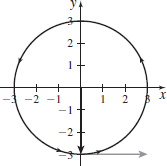
\mathbf{r}(t)=4\sin t\mathbf{i}+4\cos t \mathbf{j}
\mathbf{r}(t)=2\cos t\mathbf{i}-3\sin t\mathbf{j}
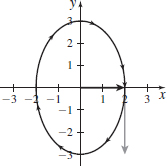
\mathbf{r}(t)=-\cos t\mathbf{i}+2\sin t\mathbf{j}
In Problems 95–98, the position of an object at time t it is given.
(a) Eliminate the parameter t to find y as a function of x.
(b) Graph \mathbf{r}=\mathbf{r}(t) and indicate the orientation.
\mathbf{r}(t) =(1-t^{2})\mathbf{i}+t^{2}\mathbf{j}
- (a) y = 1-x
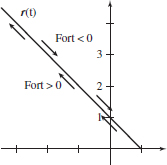
\mathbf{r}(t) =t^{2}\mathbf{i}+(4t^{2}-t^{4})\mathbf{j}
\mathbf{r}(t) =\sin ^{2}t\mathbf{i}+\tan t\mathbf{j,}\quad 0<t<\dfrac{\pi }{2}
- (a) y = \sqrt{\dfrac{x}{1-x}} for 0 < x < 1
- (b)
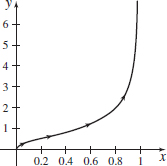
\mathbf{r}(t) =e^{t}\mathbf{i}+e^{-t}\mathbf{j}
Proof of the Sum Formula If the vector functions \mathbf{u}=\mathbf{u}(t) and \mathbf{v}=\mathbf{v}(t) are differentiable, show that \begin{equation*} \left[ \mathbf{u}(t)+\mathbf{v}(t)\right] ^{\prime} =\mathbf{u}^{\prime} (t)+ \mathbf{v}^{\prime} (t) \end{equation*}
See Student Solutions Manual.
Proof of the Dot Product Formula If the vector functions \mathbf{u}=\mathbf{u}(t) and \mathbf{v}=\mathbf{v}(t) are differentiable, show that \begin{equation*} \left[ \mathbf{u}(t)\,{\cdot}\, \mathbf{v}(t)\right] ^{\prime} =\mathbf{u}^{\prime} (t)\,{\cdot}\, \mathbf{v}(t)+\mathbf{u}(t)\,{\cdot}\, \mathbf{v}^{\prime} (t) \end{equation*}
Proof of the Cross Product Formula If the vector functions \mathbf{u}=\mathbf{u}(t) and \mathbf{v}=\mathbf{v}(t) in space are differentiable, show that \begin{equation*} \left[ \mathbf{u}(t)\times \mathbf{v}(t)\right] ^{\prime} =\mathbf{u}^{\prime} (t)\times \mathbf{v}(t)+\mathbf{u}(t)\times \mathbf{v}^{\prime} (t) \end{equation*}
See Student Solutions Manual.
Proof of the Chain Rule If the vector function \mathbf{v}=\mathbf{v}(t) is differentiable and the real function y=f(t) is differentiable, show that \begin{equation*} \dfrac{d}{dt}\mathbf{v}\left( f(t) \right) =\mathbf{v}^{\prime} (f(t) )f^{\prime} (t) \end{equation*}
The derivative of a cross product is not commutative. Give an example of two vector functions that demonstrate this fact.
Answers will vary.
Suppose the vector function \mathbf{r}=\mathbf{r}(t) is twice differentiable; show that [ \mathbf{r}(t)\times \mathbf{r}^{\prime}(t)] ^{\prime} =\mathbf{r}(t)\times \mathbf{r}^{\prime \prime} (t).
Show that \lim\limits_{t\rightarrow t_{\hbox{0}}}\mathbf{r}(t)=\mathbf{L} if and only if \lim\limits_{t\rightarrow t_{\hbox{0}}}\left\Vert \mathbf{r}(t)-\mathbf{L}\right\Vert =0.
See Student Solutions Manual.
If the vector function \mathbf{r=r}(t) is differentiable, show that \dfrac{d}{dt}\left\Vert \mathbf{r}(t)\right\Vert\; =\dfrac{\mathbf{r}(t)\,{\cdot}\, \mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}(t)\right\Vert }. Use this result to show that \left\Vert \mathbf{r}(t)\right\Vert is constant if and only if \mathbf{r}(t)\,{\cdot}\, \mathbf{r}^{\prime} (t)=0 for all t.
Challenge Problems
If the vector function \mathbf{r} is differentiable, show that \begin{equation*} \frac{d}{dt}\frac{\mathbf{r}(t)}{\left\Vert \mathbf{r}(t)\right\Vert }=\frac{ \mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}(t)\right\Vert }-\frac{\mathbf{r} (t)\,{\cdot}\, \mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}(t)\right\Vert ^{3}} \mathbf{r}(t) \end{equation*}
See Student Solutions Manual.
- (a) Discuss the curve C traced out by the vector function \mathbf{r}(t)=e^{t}\sin t\mathbf{i}+e^{t}\cos t\mathbf{j}+e^{t}\mathbf{k}.
- (b) Name the surface on which the curve C lies.
