11.2 Assess Your UnderstandingPrinted Page 772
Concepts and Vocabulary
True or False If a vector function r=r(t) is differentiable at t0, a<t0<b, and P0 is the point on the curve traced out by r=r(t) corresponding to t=t0, then the tangent line to the curve at t0 contains the point P0 and has the direction r(t0).
False
True or False A curve traced out by a vector function r=r(t) is called a smooth curve on the interval [a,b] if r=r(t) is continuous on the interval [a,b].
False
True or False If C is a smooth curve traced out by a vector function r=r(t), a≤t≤b, then T(t)=r′(t) is the unit tangent vector to C at t.
False
True or False If C is a smooth curve traced out by a twice differentiable vector function r=r(t), a≤t≤b, and if T is the unit tangent vector to C, then N(t)=T(t)‖ is the principal unit normal vector to C at t.
False
True or False For a smooth space curve C traced out by \mathbf{r}=\mathbf{r}(t), a\leq t\leq b, the integral \int_{a}^{b}\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert dt equals the arc length along C from t=a to t=b.
True
True or False For a smooth curve traced out by a twice differentiable vector function, the unit tangent vector is orthogonal to the principal unit normal vector.
True
Skill Building
In Problems 7–14:
- (a) Find the tangent vector to each curve at t.
- (b) Graph the curve.
- (c) Add the graph of the tangent vector to (b).
\mathbf{r}(t)=t\mathbf{i}-t^{2}\mathbf{j,} \quad t=1
- (a) \mathbf{r}\,'(1) = \mathbf{i}-2\mathbf{j}
- (b) and
- (c)
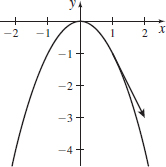
\mathbf{r}(t)=t\mathbf{i}-t^{3}\mathbf{j,} \quad t=-1
\mathbf{r}(t)=(t^{2}+1)\mathbf{i}+(1-t)\mathbf{j,} \quad t=1
- (a) \mathbf{r}\,'(1)=2\mathbf{i}-\mathbf{j}
- (b) and
- (c)
\mathbf{r}(t)=t^{3}\mathbf{i}+3t\mathbf{j,} \quad t=1
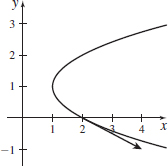
\mathbf{r}(t)=4t\mathbf{i}-\sqrt{t}\mathbf{j,} \quad t=1
- (a) r'(1) = 4{\rm {\bf i}} - \displaystyle{1 \over 2}{\rm {\bf j}}
- (b) and
- (c)
\mathbf{r}(t)=\sqrt{t}\mathbf{i}+\dfrac{1}{2}t\mathbf{j,} \quad t=4
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0
- (a) \mathbf{r}\,'(0) = \mathbf{i}-\mathbf{j}
- (b) and
- (c)

\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0
In Problems 15–22, find the tangent vector to each curve at t.
\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}-(5+t)\mathbf{k,} \quad t=0
\mathbf{r}\,'(0) = -3\mathbf{i}+2 \mathbf{j} - \mathbf{k}
\mathbf{r}(t)=(2+t)\mathbf{i}+(2-t)\mathbf{j}+3t\mathbf{k,} \quad t=0
\mathbf{r}(t)=\cos ( 2t) \mathbf{i}+\sin (2t) \mathbf{j}-5\mathbf{k,} \quad t=\dfrac{\pi }{4}
\mathbf{r}\,'\left(\dfrac{\pi}{4}\right) = -2\mathbf{i}
\mathbf{r}(t)=3\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}
773
\mathbf{r}(t)=2\cos t\mathbf{i}+\mathbf{j}+2\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}
\mathbf{r}\,' \left(\dfrac{\pi}{6}\right)= -\mathbf{i} +\sqrt{3} \mathbf{k}
\mathbf{r}(t)=2\cos ( 2t) \mathbf{i}+2\sin ( 2t) \mathbf{j}+5\mathbf{k,} \quad t=\dfrac{\pi }{2}
\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k,} \quad t=0
\mathbf{r}\,'(0) = \mathbf{i} + \mathbf{j} + \mathbf{k}
\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-e^{-t}\mathbf{k,}\quad t=0
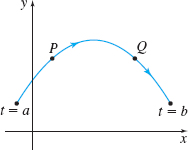
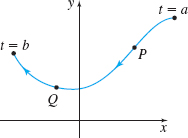
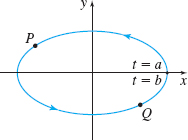
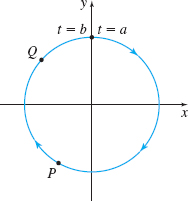
In Problems 23–26, draw the unit tangent vector \mathbf{T} and principal unit normal vector \mathbf{N} to C at the points P and Q. Be sure to use the orientation of the curve. Assume the length of a unit vector is one inch.
Figure below not drawn to scale.
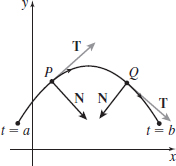
Figure below not drawn to scale.
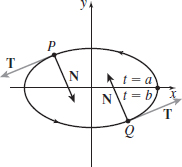
In Problems 27–42, for each vector function \mathbf{r}=\mathbf{r}( t), find the unit tangent vector \mathbf{T} and the principal unit normal vector \mathbf{N} at t.
\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j,} \quad t=1
\mathbf{T}(1) = \dfrac{\sqrt{5}}{5} \mathbf{i} + \dfrac{2\sqrt{5}}{5} \mathbf{j} and \mathbf{N}(1) = -\dfrac{2\sqrt{5}}{5} \mathbf{i}+\dfrac{\sqrt{5}}{5} \mathbf{j}
\mathbf{r}(t)=t\mathbf{i}-t^{3}\mathbf{j,} \quad t=-1
\mathbf{r}(t)=(t^{2}+1)\mathbf{i}+(1-t)\mathbf{j,} \quad t=1
\mathbf{T}(1) = \dfrac{2\sqrt{5}}{5} \mathbf{i} - \dfrac{\sqrt{5}}{5} \mathbf{j} and \mathbf{N}(1) = \dfrac{\sqrt{5}}{5} \mathbf{i} + \dfrac{2\sqrt{5}}{5} \mathbf{j}
\mathbf{r}(t)=t^{3}\mathbf{i}+3t\mathbf{j,} \quad t=1
\mathbf{r}(t)=\dfrac{2t}{t+1}\mathbf{i}-\dfrac{t^{2}}{t+1}\mathbf{j,} \quad t=1
\mathbf{T}(1) = \dfrac{2\sqrt{13}}{13} \mathbf{i} - \dfrac{3\sqrt{13}}{13} \mathbf{j} and \mathbf{N}(1) = -\dfrac{3\sqrt{13}}{13} \mathbf{i} - \dfrac{2\sqrt{13}}{13} \mathbf{j}
\mathbf{r}(t)=\sqrt{t}\mathbf{i}+\dfrac{1}{2}t\mathbf{j}, \quad t=4
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0
\mathbf{T}(0) = \dfrac{\sqrt{2}}{2} \mathbf{i} - \dfrac{\sqrt{2}}{2} \mathbf{j} and \mathbf{N}(0) = \dfrac{\sqrt{2}}{2} \mathbf{i} + \dfrac{\sqrt{2}}{2} \mathbf{j}
\mathbf{r}(t)=e^{2t}\mathbf{i}+e^{-t}\mathbf{j,} \quad t=0
\mathbf{r}(t)=(1-3t)\mathbf{i}+2t\mathbf{j}-(5+t)\mathbf{k,} \quad t=0
\mathbf{T}(0) = -\dfrac{3\sqrt{14}}{14} \mathbf{i} + \dfrac{2\sqrt{14}}{14} \mathbf{j} - \dfrac{\sqrt{14}}{14} \mathbf{k} and \mathbf{N}(0) is undefined
\mathbf{r}(t)=(2+t)\mathbf{i}+(2-t)\mathbf{j}+3t\mathbf{k,} \quad t=0
\mathbf{r}(t)=2\cos t\mathbf{i}+\mathbf{j}+2\sin t\mathbf{k,}\quad t=\dfrac{\pi }{6}
\mathbf{T}\left(\dfrac{\pi}{6}\right) = -\dfrac12 \mathbf{i} + \dfrac{\sqrt{3}}2 \mathbf{k} and \mathbf{N}\left(\dfrac{\pi}{6}\right) = -\dfrac{\sqrt{3}}2 \mathbf{i} - \dfrac12 \mathbf{k}
\mathbf{r}(t)=3\mathbf{i}+\cos t\mathbf{j}+\sin t\mathbf{k,} \quad t=\dfrac{\pi }{6}
\mathbf{r}(t)=\cos ( 2t) \mathbf{i}+\sin (2t) \mathbf{j}-5\mathbf{k,} \quad t=\dfrac{\pi }{4}
\mathbf{T}\left(\dfrac{\pi}{4}\right) = -\mathbf{i} and \mathbf{N}\left(\dfrac{\pi}{4}\right) = -\mathbf{j}
\mathbf{r}(t)=2\cos ( 2t) \mathbf{i}+2\sin ( 2t) \mathbf{j}+5\mathbf{k,} \quad t=\dfrac{\pi }{2}
\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k,}\quad t=0
\mathbf{T}(0) = \dfrac{\sqrt{3}}{3} \mathbf{i} + \dfrac{\sqrt{3}}{3} \mathbf{j} + \dfrac{\sqrt{3}}{3} \mathbf{k} and {\rm {\bf N}}(0) = -\dfrac{\sqrt{2}}{2}{\rm {\bf i}} +\dfrac{\sqrt{2}}{2}{\rm {\bf j}}
\mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j}-e^{-t}\mathbf{k,} \quad t=0
In Problems 43–54, find the arc length s of each vector function.
\mathbf{r}(t)=t\mathbf{i}+(t^{3/2}+1)\mathbf{j} from t=1 to t=8
s=\dfrac{1}{27} \left( 76^{3/2}-13^{3/2}\right)
\mathbf{r}(t)=t\mathbf{i}+t^{3/2}\mathbf{j} from t=0 to t=4
\mathbf{r}(t)=8t\mathbf{i}+\dfrac{t^{6}+2}{t^{2}}\mathbf{j} from t=1 to t=2
s= \dfrac{33}2
\mathbf{r}(t)=t\mathbf{i}+(1-t^{2/3})^{3/2}\mathbf{j} from t= \dfrac{1}{8} to t=1
\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+t\mathbf{k} from t=0 to t=1
s = \sqrt{6}
\mathbf{r}(t)=2t\mathbf{i}+t\mathbf{j}+3t\mathbf{k} from t=1 to t=3
\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos (2t) \mathbf{j}+t\mathbf{k} from t=0 to t=\pi
s = \sqrt{5} \pi
\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+bt\mathbf{k} from t=0 to t=2\pi
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}t\mathbf{k} from t=0 to t=1
s = e - \dfrac1e
\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k} from t=0 to t=\dfrac{\pi }{2}
\mathbf{r}(t)=e^{t}\cos t\mathbf{i}+e^{t}\sin t\mathbf{j}+e^{t}\mathbf{k} from t= 0 to t=2\pi
s = \sqrt{3} (e^{2\pi} - 1)
\mathbf{r}(t)=t^{2}\mathbf{i}-2\sqrt{2}\ t\mathbf{j}+(t^{2}-1)\mathbf{k} from t=0 to t=1
![]() In Problems 55–58,
In Problems 55–58,
- (a) Graph the curve traced out by the vector function \mathbf{r=\mathbf{r}(t)}.
- (b) Find the indicated arc length.
\mathbf{r}( t) =3\sin t\mathbf{i}-4\cos t\mathbf{j} from t=0 to t=\pi
- (a)

- (b) s \approx 11.052
\mathbf{r}( t) =5\cos t\mathbf{i}+3\sin t\mathbf{j} from t=0 to t=\dfrac{\pi }{2}
\mathbf{r}( t) =2\sin t\mathbf{i}+4\cos (2t) \mathbf{j} from t=0 to t= {2\pi}
- (a)
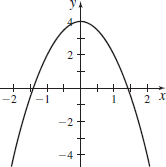
- (b) s \approx 33.637
\mathbf{r}( t) =4\sin ( 2t) \mathbf{i}-6\cos t\,\mathbf{j} from t=0 to t=\dfrac{\pi }{2}
Applications and Extensions
Find all the points on the curve traced out by \mathbf{r} (t)=t^{2}\mathbf{i}+(t^{2}-1)\mathbf{j}-t\mathbf{k} at which \mathbf{r}(t) and its tangent vector are orthogonal.
\dfrac14\mathbf i - \dfrac34\mathbf j +\dfrac12 \mathbf k, - \mathbf j, \dfrac14\mathbf i - \dfrac34\mathbf j -\dfrac12 \mathbf k
Find the angle between the helix traced out by \mathbf{r}( t) =\cos t\mathbf{i}+t\mathbf{j}+\sin t\mathbf{k} and the y-axis.
The helix defined by \mathbf{r}(t)=3\sin t\mathbf{i}+3\cos t\mathbf{j}+4t\mathbf{k} and the direction \mathbf{k} meet at a constant angle. Find the angle to the nearest degree.
\theta \approx 37^\circ
The helix defined by \mathbf{r}(t)=2\cos t\mathbf{i}+2\sin t\mathbf{j}+t\mathbf{k} and the direction \mathbf{k} meet at a constant angle. Find the angle to the nearest degree.
In Problems 63–66, find the angle between the tangent vectors to the curves traced out by \mathbf{r}_{1}(t_{1}) and \mathbf{r}_{2}(t_{2}) at the point of intersection given.
\mathbf{r}_{1}(t_{1})=t_{1}\mathbf{i}+\sin \left( \pi t_{1}\right) \mathbf{j}+\mathbf{k} and \mathbf{r}_{2}(t_{2})=\mathbf{i}+t_{2}\mathbf{j}+\left( 1+t_{2}\right) \mathbf{k} at \left( 1,0,1\right)
\mathbf{r}_{1}(t_{1})=\sin \left( 2t_{1}\right) \mathbf{i}+\sin t_{1}\mathbf{j}+t_{1}\mathbf{k} and \mathbf{r}_{2}(t_{2})=t_{2}^{2}\mathbf{i}+t_{2}\mathbf{j}+t_{2}^{3}\mathbf{k} at \left( 0,0,0\right)
\mathbf{r}_{1}(t_{1})=(e^{t_{1}}-1)\mathbf{i}-\cos \left( \pi t_{1}\right) \mathbf{j}+t_{1}\mathbf{k} and \mathbf{r}_{2}(t_{2})=(1-t_{2})\mathbf{i}-\mathbf{j}+(t_{2}-1)\mathbf{k} at (0,-1,~0)
\theta = 90^\circ
774
\mathbf{r}_{1}(t_{1})=t_{1}^{2}\mathbf{i}-( t_{1}-3) \mathbf{j}-( t_{1}-3) \mathbf{k} and \mathbf{r}_{2}(t_{2})=\big(t_{2}^{2}+3\big)\mathbf{i}-(t_{2}-2) \mathbf{j}+t_{2}\mathbf{k} at (4,1,1)
If \mathbf{r}=\mathbf{r}( t) is a vector function in space that is twice differentiable, then the cross product of the unit tangent vector and the principal unit normal vector, \mathbf{T}\times \mathbf{N}, defines a third unit vector \mathbf{B}( t). This vector \mathbf{B}, called the binormal vector, is orthogonal to both the unit tangent vector \mathbf{T} and the principal unit normal vector \mathbf{N}, as shown in the figure.
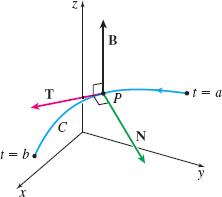
In Problems 67–70, find the unit tangent vector \mathbf{T}, the principal unit normal vector \mathbf{N}, and the binormal vector \mathbf{B} to each vector function.
\mathbf{r}(t)=t^{2}\mathbf{i}-( t-3) \mathbf{j}-( t-3) \mathbf{k}
\mathbf{T}(t) = \dfrac{2t}{\sqrt{4t^2+2}}\mathbf{i} - \dfrac{1}{\sqrt{4t^2+2}} \mathbf{j} - \dfrac{1}{\sqrt{4t^2+2}} \mathbf{k}, \mathbf{N}(t) = \dfrac{1}{\sqrt{2t^2+1}} \mathbf{i} + \dfrac{t}{\sqrt{2t^2+1}}\mathbf{j} + \dfrac{t}{\sqrt{2t^2+1}}\mathbf{k}, and \mathbf{B}(t) = -\dfrac{\sqrt{2}}{2} \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}
\mathbf{r}(t)=\left( t+5\right) \mathbf{i}-\left( t+5\right) \mathbf{j}+t^{2}\mathbf{k}
\mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k}
\mathbf{T}(t) = -\dfrac{\sqrt{2}}{2} \sin t \mathbf{i} + \dfrac{\sqrt{2}}{2} \cos t \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}, \mathbf{N}(t) = -\cos t \mathbf{i} - \sin t \mathbf{j}, and \mathbf{B}(t) = \dfrac{\sqrt{2}}{2} \sin t \mathbf{i} - \dfrac{\sqrt{2}}{2} \cos t \mathbf{j} + \dfrac{\sqrt{2}}{2} \mathbf{k}
\mathbf{r}(t)=2\sin t\mathbf{i}+2\cos t\mathbf{j}+3t\mathbf{k}
Suppose the vector function \mathbf{r=r}(t) in space is differentiable and has a nonzero tangent vector at t_{0}. Find the direction cosines for the tangent vector at t_{0}.
\cos \alpha = \dfrac{x'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}, \cos \beta = \dfrac{y'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}, \cos \gamma = \dfrac{z'(t_0)}{\left\Vert\mathbf{r}\,'(t_0)\right\Vert}
Show that at any point, the tangent vectors to a helix \mathbf{r}(t)=a\cos t\mathbf{i}+a\sin t\mathbf{j}+bt\mathbf{k}, where a and b are real numbers, intersect the direction of the z-axis at a constant angle.
Challenge Problems
Use Simpson's Rule with n=4 to approximate the length of the curve \mathbf{r}(t)=t^{2}\mathbf{i}+t^{3}\mathbf{j}+(2t+3)\mathbf{k}, 0\leq t\leq 2.
s \approx 10.516
- (a) Approximate the arc length of \mathbf{r}( t) =3\sin t\mathbf{i}-4\cos t\mathbf{j} from t=0 to t=\pi using Simpson's Rule with n=4.
- (b) Approximate the arc length of \mathbf{r}( t)=3\sin t\mathbf{i}-4\cos t\mathbf{j} from t=0 to t=\pi using the Trapezoidal Rule with n=6.
- (c) Compare the answers to (a) and (b) to the result given by technology (see Problem 55).
- (a) Approximate the arc length of \mathbf{r}( t) =2\sin t\mathbf{i}+4\cos ( 2t)\mathbf{j} from t=0 to t=2\pi using Simpson's Rule with n=4.
- (b) Approximate the arc length of \mathbf{r}( t) =2\sin t\mathbf{i}+4\cos ( 2t)\mathbf{j} from t=0 to t=2\pi using the Trapezoidal Rule with n=6.
- (c) Compare the answers to (a) and (b) to the result given by technology (see Problem 57).
- (a) s = \dfrac{4\pi}3 \approx 4.189
- (b) s \approx 33.510
- (c) See the Student Solutions Manual
Approximate the length of the curve \mathbf{r}(t)=\dfrac{1}{3}t^{3}\mathbf{i}+(t-1)\mathbf{j}+2\mathbf{k}, 0\leq t\leq \dfrac{1}{2}, correct to three decimal places, by expanding the integrand in a power series.