11.3 Assess Your UnderstandingPrinted Page 782
Concepts and Vocabulary
Multiple Choice If a smooth curve C is traced out by the vector function r=r(t), a≤t≤b, then the parameter t is the arc length if and only if [(a) ‖, (b) \left\Vert \mathbf{r}^{\prime}(t)\right\Vert\;=0, (c) \left\Vert \mathbf{r}^{\prime\prime}(t)\right\Vert\;=1, (d) \left\Vert \mathbf{r}^{\prime}(t)\right\Vert\;=1] for all t.
(d)
True or False The curvature \kappa of a straight line equals the slope of the line.
False
True or False The curvature \kappa of a circle equals the radius of the circle.
False
True or False The curvature \kappa of a twice differentiable smooth curve C equals the magnitude of the rate of change of the unit tangent vector \mathbf{T} with respect to arc length.
True
True or False The curvature \kappa of a twice differentiable smooth curve C: \mathbf{r}=\mathbf{r}(t) is \kappa\;=\;\dfrac{\left\Vert \mathbf{r}^{\prime} (t) \times \mathbf{r} ^{\prime \prime} (t) \right\Vert }{\left\Vert \mathbf{r}(t) \right\Vert ^{3}}.
False
The curvature of a twice differentiable function y=f(x) is \kappa = _______.
\dfrac{|f''(x)|}{(1+[f'(x)]^2)^{3/2}}
The curvature of the circle x^{2}+\left( y-2\right) ^{2}=9 is \kappa = _______.
\dfrac13
True or False The radius \rho of the osculating circle at a point P of a smooth curve C equals \kappa, provided \kappa \neq 0.
False
Skill Building
In Problems 9–18, determine whether the parameter used for each curve is the arc length along the curve.
\mathbf{r}(t)=4\cos t\mathbf{i}-4\sin t\mathbf{j},\quad 0\leq t\leq 2\pi
No
\mathbf{r}(t)=\sin (3t)\mathbf{i}+\cos (3t)\mathbf{j,} \quad 0\leq t\leq 2\pi
\mathbf{r}(t)=t^{2}\mathbf{i}+t\mathbf{j},\quad 0\leq t\leq 4
No
\mathbf{r}(t)=t\mathbf{i}+t^{3}\mathbf{j,}\quad 0\leq t\leq 2
\mathbf{r}(t)=(2t+1)\mathbf{i}+(3t-2)\mathbf{j},\quad 0\leq t\leq 5
No
\mathbf{r}(t)=\mathbf{i}+t\mathbf{j},\quad 0\leq t\leq 1
\mathbf{r}(t)=\left( \dfrac{2}{\sqrt{13}}t+1\right) \mathbf{i}+\left( \dfrac{3}{\sqrt{13}}t-2\right) \mathbf{j}, 0\leq t\leq 5\sqrt{13}
Yes
\mathbf{r}(t)=\mathbf{i}+t^{2}\mathbf{j},\quad 0\leq t\leq 1
\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+t\mathbf{k}
No
\mathbf{r}(t)=a\sin t\mathbf{i}+a\cos t\mathbf{j}+\sqrt{1-a^{2}}\kern1pt t\mathbf{k}
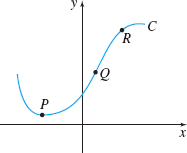
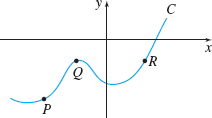
In Problems 19 and 20, rank the curvature of each curve at points P, Q, and R from greatest to least.
P R Q
In Problems 21–26, find the curvature \kappa of each plane curve traced out by the vector function \mathbf{r}=\mathbf{r}(t).
\mathbf{r}(t)=t^{2}\mathbf{i}+\dfrac{2}{t}\mathbf{j}
\kappa = \dfrac{3t^4}{2(t^6+1)^{3/2}}
\mathbf{r}(t)=2t\mathbf{i}+t^{3}\mathbf{j}
\mathbf{r}(t)=2\sin t \mathbf{i}+2\cos t\mathbf{j}
\kappa = \dfrac12
\mathbf{r}(t)=\cos t\mathbf{i}+2\sin t\mathbf{j}
\mathbf{r}(t)=(3t-t^{3})\mathbf{i}+3t^{2} \mathbf{j}
\kappa = \dfrac{2}{3(t^2+1)^2}
\mathbf{r}(t)=(3t-t^{3})\mathbf{i}+(3t+t^{3})\mathbf{j}
783
In Problems 27–34, find the curvature \kappa of each space curve traced out by the vector function \mathbf{r}=\mathbf{r}(t).
\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+t\mathbf{k}
\kappa = 0
\mathbf{r}(t)=2t\mathbf{i}+t\mathbf{j}+3t\mathbf{k}
\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos ( 2t) \mathbf{j}+t\mathbf{k}
\kappa = \dfrac45
\mathbf{r}(t)=\sin t\mathbf{i}\,{+}\,\cos t\mathbf{j}\,{+}\,bt\mathbf{k}
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}t\mathbf{k}
\kappa = \dfrac{\sqrt{2}e^{2t}}{(e^{2t}+1)^2}
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{2t}\mathbf{j}+e^{-t}\mathbf{k}
\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k}
κ = 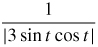
\mathbf{r}(t)=4\cos ^{3}t\mathbf{i}+ 3\mathbf{j} + 4\sin^{3}t\mathbf{k}
In Problems 35–44, find the curvature \kappa of the graph of each function at the indicated point.
y=x^{2} at (1,1)
\kappa=\dfrac{2\sqrt{5}}{25}
y=2x-x^{2} at (1,1)
y=x^{2}-x^{3} at (1,0)
\kappa= \sqrt{2}
y=x^{-3/2} at (1,1)
y=\sqrt{x} at \big(2,\sqrt{2}\big)
\kappa= \dfrac2{27}
y=\dfrac{1}{\sqrt{x}} at (1,1)
4x^{2}+9y^{2}=36 at (0,2)
\kappa= \dfrac29
y=\sec x-1 at \left(\! \dfrac{\pi}{4}, \sqrt{2}-1\!\right)
y=e^{x} at (0,1)
\kappa= \dfrac{\sqrt{2}}{4}
y=\ln (x+1) at ( 2,\ln 3)
In Problems 45–52, find the radius of the osculating circle at the indicated point.
y=x^{3}-6x at (1,-5)
\rho = \dfrac{5\sqrt{10}}3
y=\dfrac{1}{x^{2}} at (-1,1)
y=\sin x at \left( \dfrac{\pi }{2},1\right)
\rho = 1
y=e^{-x} at (0,1)
x^{2}+xy+y^{2}=3 at (1,1)
\rho = 3\sqrt{2}
y^{2}-y+x=0 at (0,0)
y=\ln ( \sec x) at \left(\dfrac{\pi }{4}, \ln \sqrt{2}\right)
\rho = \sqrt{2}
y=\cosh x at (0,1)
In Problems 53–62, find the radius of the osculating circle at the point corresponding to t on the curve C traced out by the vector function \mathbf{r}=\mathbf{r}(t).
\mathbf{r}(t)=3t^{2}\mathbf{i}+(3t-t^{3})\mathbf{j,}\quad t=1
\rho = 6
\mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}+t^{3}\mathbf{k},\quad t=1
\mathbf{r}(t)=\sin t\mathbf{i}+\cos ( 2t) \mathbf{j},\quad t=\dfrac{\pi }{4}
\rho = \dfrac{27}4
\mathbf{r}(t)=\sin t\mathbf{i}+\cos t\mathbf{j}+bt\mathbf{k,}\quad b>0,\quad t=\dfrac{\pi }{4}
\mathbf{r}(t)=\sin ( 2t) \mathbf{i}+\cos ( 2t) \mathbf{j}+t\mathbf{k,}\quad t=\dfrac{\pi }{4}
\rho = \dfrac54
\mathbf{r}(t)=\cos ^{3}t\mathbf{i}+\sin ^{3}t\mathbf{j}+\mathbf{k,}\quad t=\dfrac{\pi }{3}
\mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+\sqrt{2}\kern1ptt\mathbf{k},\quad t=0
\rho = 2\sqrt2
\mathbf{r}(t)=a(3t-t^{3})\mathbf{i}+3at^{2}\mathbf{j}+a(3t+t^{3})\mathbf{k,}\quad a>0, \quad t=1
\mathbf{r}(t)=4a\cos ^{3}t\mathbf{i}+4a\sin ^{3}t\mathbf{j}+3a\cos ( 2t) \mathbf{k,}\quad a>0,\quad t=\dfrac{\pi }{4}
\rho = 12a
\mathbf{r}(t)=t\mathbf{i}+2t\mathbf{j}+\sqrt{1-5t^{2}}\kern1pt\mathbf{k},\quad -\dfrac{\sqrt{5}}{5} < t< \dfrac{\sqrt{5}}{5},\quad t=0
Applications and Extensions
Radius of Curvature Show that the radius of curvature of the parabola y=ax^{2}+bx+c is a minimum at its vertex.
See the Student Solutions Manual.
Radius of Curvature Show that the radii of curvature at the ends of the axes of the ellipse b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2} are \dfrac{b^{2}}{a} and \dfrac{a^{2}}{b},\quad a>0, b>0.
Maximum Curvature Find the point on the curve y=\ln x at which the curvature is maximum.
\left(\dfrac{\sqrt{2}}{2}, \ln \dfrac{\sqrt{2}}{2} \right)
Maximum Curvature Find the point on the curve y=e^{x} at which the curvature is maximum.
Maximum Curvature Find the point(s) on the curve y=\dfrac{1}{3}x^{3} at which the curvature is maximum.
\left(\pm\left(\dfrac{1}{5}\right)^{{1}/{4}},\;\pm\dfrac{1}{3}\left(\dfrac{1}{5}\right)^{{3}/{4}}\right)
Maximum Curvature Find the point(s) on the curve y=\sin x at which the curvature is maximum.
Maximum Curvature Find \alpha >0 so that \mathbf{r} (t)= \alpha \cos t\mathbf{i} + \alpha \sin t\mathbf{j}+t\mathbf{k} has maximum curvature.
\alpha=1
Curvature of a Plane Curve What is the curvature at a point of inflection of a plane curve?
Curvature of a Catenary Show that the curvature of the catenary y=a\cosh \dfrac{x}{a}, a>0, at any point (x,y) is \dfrac{a}{y^{2}}.
See the Student Solutions Manual.
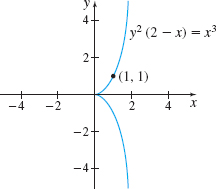
Curvature of a Cissoid Find the curvature of the cissoid y^{2}(2-x)=x^{3} at the point (1,1). See the figure.
Curvature of a Cycloid Find the curvature of the cycloid x( \theta)\;=\;\theta -\sin \theta and y( \theta )\;=\;1-\cos \theta at the highest point of an arch. See the figure.
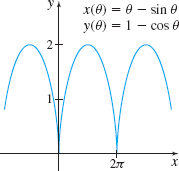
\kappa = \dfrac14
- (a) Find the curvature of the curve \mathbf{r} (t)=(1-t^{3})\mathbf{i}+t^{2}\mathbf{j}.
- (b)
 Graph \mathbf{r}=\mathbf{r}(t). Where is the curvature undefined? Do you see any geometric reason for this?
Graph \mathbf{r}=\mathbf{r}(t). Where is the curvature undefined? Do you see any geometric reason for this?
Curvature of a Spiral Find the curvature of the spiral \mathbf{r}(t)=e^{-t}\cos t\mathbf{i}+e^{-t}\sin t\mathbf{j} shown in the figure. How does the curvature behave when t\rightarrow \infty? Do you see any geometric reason for this?
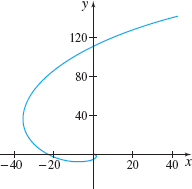
\kappa = \dfrac{e^t \sqrt{2}}{2}. As t \to \infty, \kappa \to \infty as the graph curves more and more tightly around the origin.
784
Curvature Find the curvature \kappa of the curve \mathbf{r}(t)=2a\cos t\mathbf{i}+2a\sin t\mathbf{j}+bt^{2}\mathbf{k},\qquad a>0, b>0.
Curvature Show that the curvature of an ellipse \dfrac{x^{2}}{ a^{2}}+\dfrac{y^{2}}{b^{2}}=1, a> b, is a maximum at the points \left( \pm a,0\right) and is a minimum at the points \left( 0,\pm b\right).
Source: Contributed by the students at the University of Missouri.
See the Student Solutions Manual.
Curvature Show that the circular helix \mathbf{r}( t)\;=\;a\cos t\mathbf{i}+a\sin t\mathbf{j}+t\mathbf{k} has constant curvature.
Source: Contributed by the students at the University of Missouri.
Write a vector equation for the curve C traced out by \mathbf{r}(t)=2t\mathbf{i}+(2t-1)\mathbf{j}+t\mathbf{k}, 0\leq t\leq 2, using arc length s as the parameter. [Hint: For each t, 0\leq t\leq 2, calculate the length s(t) of the curve from 0 to t.]
\mathbf{r}(s) = \dfrac{2s}{3} \mathbf{i} + \dfrac{2s-3}{3} \mathbf{j} + \dfrac{s}{3} \mathbf{k}, 0 \leq s \leq 6
Compare the solutions of Problems 13 and 15. Then show how to change the parameter t of the line \mathbf{r}(t)=(at+b)\mathbf{i}+(ct+d) \mathbf{j}, where either a\neq 0 or c\neq 0, to one that is arc length as measured along the line.
Suppose a smooth curve C is traced out by a twice differentiable vector function \mathbf{r}=\mathbf{r}(t), a\leq t\leq b. If the curvature \kappa \neq 0 at a point P on C, show that the position vector \mathbf{C} of the center of the osculating circle at P is given by \begin{equation*} \mathbf{C}(t)=\mathbf{r}(t)+\rho \mathbf{N}(t) \end{equation*} where \mathbf{N} is the principal unit normal vector to C at P, and \rho\;=\;\dfrac{1}{\kappa }.
See the Student Solutions Manual.
Use the result of Problem 81 to find the center and radius of the osculating circle for the helix \mathbf{r}(t)=a\sin t\mathbf{i}+a\cos t\mathbf{j}+a^{2}t\mathbf{k}, a>0; \begin{equation*} {\bf (a)}\enspace at\enspace t=\dfrac{\pi }{2}.\qquad {\bf (b)}\enspace at\enspace t=\pi. \end{equation*}
Use the following discussion for Problems 83–87. Suppose C is a smooth curve traced out by the twice differentiable vector function \mathbf{r}=\mathbf{r}(s), \ a\leq s\leq b, where s is arc length as measured along C . Define the binormal vector \mathbf{B} of C as \mathbf{B}(s)=\mathbf{T}(s)\times \mathbf{N}(s).
Show that the three vectors \mathbf{T}, \mathbf{N}, and \mathbf{B} form a collection of mutually orthogonal unit vectors at each point on C.
See the Student Solutions Manual.
Show that \dfrac{d\mathbf{T}}{ds}=\kappa (s)\mathbf{N}(s).
Show that \dfrac{d\mathbf{B}}{ds} is orthogonal to both \mathbf{B}(s) and \mathbf{T}(s).
See the Student Solutions Manual.
If the torsion \tau (s) of C is defined by the equation \dfrac{d\mathbf{B}}{ds}=-\tau \mathbf{N}, show that \dfrac{d\mathbf{N}}{ds}=\tau \mathbf{B}-\kappa \mathbf{T}.
Find \kappa, \mathbf{T}, \mathbf{N}, and \mathbf{B} for \mathbf{r}(s)=\dfrac{1}{\sqrt{2}}\left[ \sin s\mathbf{i}+\cos s\mathbf{j}+s\mathbf{k}\right].
\kappa=\dfrac{\sqrt{2}}{2}, \mathbf{T}(s)=\dfrac{\sqrt{2}}{2}\cos{s}\mathbf{i}-\dfrac{\sqrt{2}}{2}\sin{s}\mathbf{j}+\dfrac{\sqrt{2}}{2}\mathbf{k}, \mathbf{N}(s)=-\sin{s}\mathbf{i}-\cos{s}\mathbf{j}, and \mathbf{B}(s)=\dfrac{\sqrt{2}}{2}\cos{s}\mathbf{i}-\dfrac{\sqrt{2}}{2}\sin{s}\mathbf{j}-\dfrac{\sqrt{2}}{2}\mathbf{k}
Challenge Problems
Curvature of a Polar Curve Show that the formula for the curvature of a polar curve r=f(\theta ) is \begin{eqnarray*} \\[-24pt] \kappa\;=\;\frac{\left\vert r^{2}+2\!\left( \dfrac{dr}{d\theta }\right) ^{2}-r\left( \dfrac{d^{2}r}{d\theta ^{2}}\right) \right\vert }{\left[ r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}\right] ^{3/2}} \end{eqnarray*}
In Problems 89–94, use the result of Problem 88 to find the curvature of each polar curve.
r=2\cos ( 2\theta ) at \theta\;=\;\dfrac{\pi }{12}
\kappa = \dfrac{23}{7^{3/2}}
r=e^{a\theta } at \theta\;=\;\dfrac{\pi }{2}, a>0
r=a\theta at \theta\;=\;1 and a>0
\kappa = \dfrac{3\sqrt{2}}{ 4a}
r=1-\cos \theta at \theta\;=\;0
r=3-2\sin \theta at \theta\;=\;\dfrac{\pi }{6}
\kappa = \dfrac{8\sqrt{7}}{49 }
r=2+3\cos \theta at \theta\;=\;\dfrac{\pi }{3}
Use the figure below to show that the coordinates (h,k) of the center of curvature of y=f(x) are \begin{equation*} h=x-\rho \sin \phi\qquad k=y+\rho \cos \phi \end{equation*} where \rho is the radius of curvature. Show that \begin{equation*} \sin \phi\;=\;\frac{y^{\prime} }{\sqrt{1+( y^{\prime} ) ^{2}}}\qquad \hbox{and}\qquad \cos \phi\;=\;\frac{1}{\sqrt{1+( y^{\prime} ) ^{2}}} \end{equation*} so \begin{equation*} h=x-\frac{y^{\prime} \left[ 1+( y^{\prime} ) ^{2}\right] }{y^{\prime \prime}}\qquad \hbox{and}\qquad k=y+\frac{1+( y^{\prime} ) ^{2}}{y^{\prime \prime} } \end{equation*}
See the Student Solutions Manual.
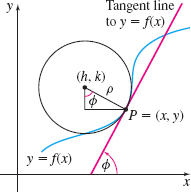
In Problems 96–100, use the result obtained in Problem 95 to find the center of curvature of each function.
y=x^{2} at x=1
y=\sin x at x=\dfrac{\pi }{2}
(h,k) = \left( \dfrac{\pi}2,0 \right)
y=\dfrac{x}{x+1} at (0, 0)
x^{3}+y^{3}=4xy at (2, 2)
(h,k) = \left(\dfrac74, \dfrac74\right)
xy=4 at x=2
As a point P moves along a curve C, the center of curvature corresponding to P traces out a curve C_{1} called the evolute of C; conversely, C is the involute of C_{1}. Show that parametric equations of the evolute of y=\dfrac{1}{2}x^{2} are h=-x^{3}, k=\dfrac{3}{2}x^{2}+1. Then eliminate the parameter x to obtain \begin{equation*} h^{2}=\frac{8}{27}\left( k-1\right) ^{3} \end{equation*}
See the Student Solutions Manual.
Refer to Problem 101. Find parametric equations and a rectangular equation for the evolute of \mathbf{r}( t)\;=\;a\cos t\mathbf{i}+b\sin t\mathbf{j}, a>0, b>0, 0\leq t\leq 2\pi .