Functions of Several Variables

12.5 Assess Your Understanding
Printed Page 856

Concepts and Vocabulary

True or False If a differentiable function $z$ is defined implicitly by the equation $F(x,y,z)=0$ , then $\dfrac{\partial z}{ \partial x}=\dfrac{F_{x}(x,y,z)}{F_{z}(x,y,z)},$ provided $F_{z}(x,y,z)\neq 0.$

False

True or False If $x=x( t)$ and $y=y( t)$ are differentiable functions of $t$ and if $z=f(x,y)$ is a differentiable function of $x$ and $y,$ then $\dfrac{dz}{dt}=\dfrac{ \partial z}{\partial x}+\dfrac{\partial z}{\partial y}.$

False

Skill Building

Answers to Problems 3–40 are given in final form and in mixed form.

In Problems 3–14, find $\dfrac{dz}{dt}$ using Chain Rule I.

$z=x^{2}+y^{2}$ , $x=\sin t$ , $y=\cos (2t)$

$\dfrac{dz}{dt}=(2x)(\cos t)-4y\sin(2t)=2\sin t\cos t-4\sin(2t)\cos(2t)$

$z=x^{2}-y^{2}$ , $x=\sin ( 2t)$ , $y=\cos t$

$z=x^{2}+y^{2}$ , $x=te^{t}$ , $y=te^{-t}$

$\dfrac{dz}{dt}=(2x)(te^t+e^t)+(2y)(-te^{-t}+e^{-t})=2t^2e^{2t}+2te^{2t}-2t^2e^{-2t}+2te^{-2t}$

$z=x^{2}-y^{2}$ , $x=te^{-t}$ , $y=t^{2}e^{-t}$

$z=e^{u}\sin v$ , $u=\sqrt{t}$ , $v=\pi t$

$\dfrac{dz}{dt}=\dfrac{e^u\sin v}{2\sqrt{t}}+(e^u\cos v)(\pi)=\dfrac{e^{\sqrt{t}}\sin(\pi t)}{2\sqrt{t}}+\pi e^{\sqrt{t}}\cos (\pi t)$

$z=e^{u/v}$ , $u=\sqrt{t}$ , $v=t^{3}+1$

$z=e^{u/v}$ , $u=te^{t}$ , $v=e^{t^{2}}$

$\dfrac{dz}{dt}=\dfrac{e^{u/v}(te^t+e^t)}v- \dfrac{ue^{u/v}\big(2te^{t^2}\big)}{v^2} =\dfrac{te^{t+te^{t-t^2}}+e^{t+te^{t-t^2}}}{e^{t^2}}- \dfrac{2t^2e^{t+t^2+te^{t-t^2}}}{e^{2t^2}}$

$z=\ln (uv)$ , $u=t^{5}$ , $v=\sqrt{t+1}$

$z=e^{x^{2}+y^{2}}$ , $x=\sin (2t)$ , $y=\cos t$

$\begin{eqnarray*}\dfrac{dz}{dt}&=&\big(2xe^{x^2+y^2}\big)(2\cos (2t))-(2ye^{x^2+y^2})(\sin t)\\ &=&4\sin(2t)\cos(2t)e^{\sin^2(2t)+\cos^2t}-2\sin t\cos te^{\sin^2(2t)+\cos^2t}\end{eqnarray*}$

$z=e^{x^{2}-y^{2}}$ , $x=\sin (2t)$ , $y=\cos (2t)$

$z=\dfrac{xy}{x^{2}+y^{2}}$ , $x=\sin t$ , $y=\cos t$

$\dfrac{dz}{dt}=\left(\dfrac{y(-x^2+y^2)}{(x^2+y^2)^2}\right)(\cos t)+\left(\dfrac{x(x^2-y^2)}{(x^2+y^2)^2}\right)(-\sin t)=\cos^2t-\sin^2t$

$z=y\ln x+xy+\tan y$ , $x=\dfrac{t}{t+1}$ , $y=t^{3}-t$

In Problems 15–22, find $\dfrac{dp}{dt}$ using an extension of Chain Rule I.

$p=x^{2}+y^{2}-z^{2},$ $x=te^{t}$ , $y=te^{-t},$ $z=e^{2t}$

$\begin{eqnarray*}\dfrac{dp}{dt}&=&(2x)(te^t+e^t)+(2y)(-te^{-t}+e^{-t})-(2z)(2e^{2t})\\ &=&2t^2e^{2t}+2te^{2t}-2t^2e^{-2t}+2te^{-2t}-4e^{4t}\end{eqnarray*}$

$p=x^{2}-y^{2}-z^{2}$ , $x=te^{-t}$ , $y=t^{2}e^{-t}$ , $z=e^{-t}$

$p=e^{x}\sin y\cos z,$ $x=\sqrt{t}$ , $y=\pi t,$ $z=\dfrac{t}{2}$

$\begin{eqnarray*}\dfrac{dp}{dt}&=&(e^x\sin y \cos z)\left(\dfrac{1}{2\sqrt{t}}\right)+(e^x\cos y\cos z)(\pi)-(e^x\sin y\sin z)\left(\dfrac12\right)\\ &=&\dfrac{e^{\sqrt{t}}\sin(\pi t)\cos(t/2)}{2\sqrt{t}}+\pi e^{\sqrt{t}}\cos(\pi t)\cos(t/2)-\dfrac{e^{\sqrt{t}}\sin(\pi t)\sin(t/2)}{2}\end{eqnarray*}$

$p=\ln (xyz)$ , $x=t^{5}$ , $y=\sqrt{t+1},$ $z=t^{2}$

$p=w \ln \left( \dfrac{u}{v}\right)$ , $u=te^{t}$ , $v=e^{t^{2}},$ $w=e^{2t}$

$\dfrac{dp}{dt}=\left(\dfrac{w}{u}\right)(te^t+e^t)-\left(\dfrac{w}{v}\right)\big(2te^{t^2}\big) +\ln\left(\dfrac{u}{v}\right)(2e^{2t}) =e^{2t}+\dfrac{e^{2t}}{t}+2e^{2t}\ln t-2t^2e^{2t}$

$p=we^{u/v},$ $u=\sqrt{t}$ , $v=t^{3}+1$ , $w=e^{t}$

$p=u^{2}vw,$ $u=\sin t$ , $v=\cos t$ , $w=e^{t}$

$\dfrac{dp}{dt}=(2uvw)(\cos t)-(u^2w)(\sin t)+(u^2v)(e^t) =2e^t\sin t\cos^2t-e^t\sin^3t+e^t\sin^2t\cos t$

$p=\sqrt{uvw}$ , $u=e^{t}$ , $v=te^{t}$ , $w=t^{2}e^{2t}$

In Problems 23–34, find $\dfrac{\partial z}{\partial u}$ and $\dfrac{\partial z}{\partial v}$ using Chain Rule II.

$z=x^{2}+y^{2},$ $x=ue^{v},$ $y=ve^{u}$

$\dfrac{\partial z}{\partial u}=(2x)(e^v)+(2y)(ve^u)=2ue^{2v}+2v^2e^{2u}$ ; $\dfrac{\partial z}{\partial v}=(2x)(ue^v)+(2y)(e^u)=2u^2e^{2v}+2ve^{2u}$

$z=x^{2}-y^{2},$ $x=u\ln v,$ $y=v\ln u$

$z=e^{x}\sin y,$ $x=u^{2}v,$ $y=\ln (uv)$

$\begin{eqnarray*}\dfrac{\partial z}{\partial u}&=&(e^x\sin y)(2uv)+(e^x\cos y)\left(\dfrac1{u}\right)=2uv e^{u^2v}\sin(\ln (uv))+ \dfrac{e^{u^2v}\cos(\ln(uv))}{u};\\ \dfrac{\partial z}{\partial v}&=&(e^x\sin y)(u^2)+(e^x\cos y)\left(\dfrac{1}{v}\right)=u^2e^{u^2v}\sin(\ln(uv))+\dfrac{e^{u^2v}\cos(\ln(uv))}{v}\end{eqnarray*}$

$z=\dfrac{1}{y}\ln x,$ $x=\sqrt{uv},$ $y=\dfrac{v}{u}$

$z=\ln (x^{2}+y^{2}),$ $x=\dfrac{v^{2}}{u},$ $y=\dfrac{u}{v^{2}}$

$\begin{eqnarray*}\dfrac{\partial z}{\partial u}&=&\left(\dfrac{2x}{x^2+y^2}\right)\left(\dfrac{-v^2}{u^2}\right)+\left(\dfrac{2y}{x^2+y^2}\right) \left(\dfrac{1}{v^2}\right)=\dfrac{-2v^8}{u(u^4+v^8)}+\dfrac{2u^3}{u^4+v^8}\\ \dfrac{\partial z}{\partial v}&=&\left(\dfrac{2x}{x^2+y^2}\right)\left(\dfrac{2v}{u}\right)+\left(\dfrac{2y}{x^2+y^2}\right) \left(\dfrac{-2u}{v^3}\right)=\dfrac{4v^7}{u^4+v^8}-\dfrac{4u^4}{v(u^4+v^8)}\end{eqnarray*}$

$z=x\sin y-y\sin x,$ $x=u^{2}v,$ $y=uv^{2}$

$z=x^{2}+y^{2},$ $x=\sin (u-v),$ $y=\cos (u+v)$

$\begin{eqnarray*}\dfrac{\partial z}{\partial u}&=&(2x)(\cos(u-v))-(2y)(\sin(u+v)) =2\sin(u-v)\cos(u-v)-2\sin(u+v)\cos(u+v)\\ \dfrac{\partial z}{\partial v}&=&-(2x)(\cos(u-v))-(2y)(\sin(u+v))=-2\sin(u-v)\cos(u-v)-2\sin(u+v)\cos(u+v)\end{eqnarray*}$

$z=e^{x}+y,$ $x=\tan ^{-1}\left( \dfrac{u}{v}\right) ,$ $y=\ln (u+v)$

$z=se^{r},$ $r=u^{2}+v^{2},$ $s=\dfrac{v}{u}$

$\begin{eqnarray*}\dfrac{\partial z}{\partial u}&=&(e^r)\left(\dfrac{-v}{u^2}\right)+(se^r)(2u) =\dfrac{-ve^{u^2+v^2}}{u^2}+2ve^{u^2+v^2}\\ \dfrac{\partial z}{\partial v}&=&(e^r)\left(\dfrac1{u}\right)+(se^r)(2v) =\dfrac{e^{u^2+v^2}}{u}+\dfrac{2v^2e^{u^2+v^2}}{u}\end{eqnarray*}$

$z=\sqrt{s^{2}+r^{2}}$ , $s=\ln (uv),$ $r=\sqrt{uv}$

857

$z=xy^{2}w^{3},$ $x=2u+v,$ $y=5u-3v,$ $w=2u+3v$

$\begin{eqnarray*}\dfrac{\partial z}{\partial u}&=&2y^2w^3+10xyw^3+6xy^2w^2\\ &=&2(5u-3v)^2(2u+3v)^3+10(2u+v)(5u-3v)(2u+3v)^3+6(2u+v)(5u-3v)^2(2u+3v)^2\\ \dfrac{\partial z}{\partial v}&=&y^2w^3-6xyw^3+9xy^2w^2\\ &=&(5u-3v)^2(2u+3v)^3-6(2u+v)(5u-3v)(2u+3v)^3+9(2u+v)(5u-3v)^2(2u+3v)^2\end{eqnarray*}$

$z=x^{2}-y^{2}+w,$ $x=e^{u+v},$ $y=uv,$ $w=\dfrac{v}{u}$

In Problems 35–40, find each partial derivative.

Find $\dfrac{\partial f}{\partial u},$ $\dfrac{\partial f}{ \partial v},$ $\dfrac{\partial f}{\partial w}$ if $f(x,y,z)=x^{2}+y^{2}+z^{2},$ $x=uv$ , $y=e^{u+2v+3w}$ , $\ z=2v+3w$ .

$\begin{eqnarray*}\dfrac{\partial f}{\partial u}&=&(2x)(v)+(2y)(e^{u+2v+3w}) =2uv^2+2e^{2u+4v+6w}\\ \dfrac{\partial f}{\partial v}&=&(2x)(u)+(2y)(2e^{u+2v+3w})+(2z)(2) =2u^2v+4e^{2u+4v+6w}+4(2v+3w)\\ \dfrac{\partial f}{\partial w}&=&(2y)(3e^{u+2v+3w})+(2z)(3) =6e^{2u+4v+6w}+6(2v+3w)\end{eqnarray*}$

Find $\dfrac{\partial f}{\partial u},$ $\dfrac{\partial f}{ \partial v},$ $\dfrac{\partial f}{\partial w}$ if $f(x,y,z)=x-y^{2}+z^{2},$ $x=\sqrt{u+v}$ , $y=(u+w) \ln v$ , $\ z=2-v+3w$ .

Find $\dfrac{\partial f}{\partial u},$ $\dfrac{ \partial f}{\partial v},$ $\dfrac{\partial f}{\partial w}$ if $f(x,y,z)=x\cos y-z\cos x+x^{2}yz,$ $x=uvw,$ $y=u^{2}+v^{2}+w^{2},$ $\ z=w$ .

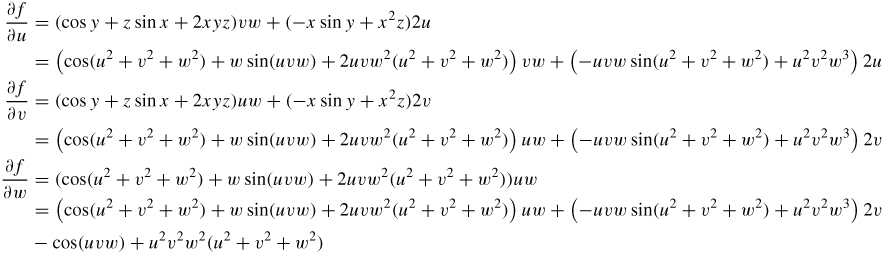
Find $\dfrac{\partial f}{\partial u},$ $\dfrac{\partial f}{ \partial v},$ $\dfrac{\partial f}{\partial w}$ if $\ f(x,y,z)=x^{2}+y^{2}$ , $x=\sin (u-v),$ $y=\cos (u+v)$ , $\ z=uw^{2}$ .

Find $\dfrac{\partial f}{\partial u},$ $\dfrac{\partial f}{ \partial v},$ $\dfrac{\partial f}{\partial w},$ $\dfrac{\partial f}{ \partial t}$ if $\ f(x,y,z)=x+2y^{2}-z^{2},$ $x=ut$ , $\ y=e^{u+2v+3w+4t}$ , $\ z=u+\dfrac{1}{2}v+4t$ .

$\begin{eqnarray*}\dfrac{\partial f}{\partial u}&=&t+4ye^{u+2v+3w+4t}-2z =t+4e^{2u+4v+6w+8t}-2(u+v/2+4t)\\ \dfrac{\partial f}{\partial v}&=&8ye^{u+2v+3w+4t}-z =8e^{2u+4v+6w+8t}-u-v/2-4t\\ \dfrac{\partial f}{\partial w}&=&12ye^{u+2v+3w+4t} =12e^{2u+4v+6w+8t}\\ \dfrac{\partial f}{\partial t}&=&u+16ye^{u+2v+3w+4t}-8z =u+16e^{2u+4v+6w+8t}-8(u+v/2+4t)\end{eqnarray*}$

Find $\dfrac{\partial f}{\partial u},$ $\dfrac{\partial f}{ \partial v},$ $\dfrac{\partial f}{\partial w},$ $\dfrac{\partial f}{ \partial t}$ if $f(x,y,z)=x^{2}+y^{2}+z,$ $x=\sin ( u+t)$ , $\ y=\cos (v-t)$ , $\ z=uw^{2}$ .

In Problems 41–46, $y$ is a function of $x$ . Find $\dfrac{dy}{dx}.$

$F(x, y)=x^{2}y-y^{2}x+xy-5=0$

$\dfrac{dy}{dx}=\dfrac{-(2xy-y^2+y)}{x^2-2xy+x}$

$F(x, y)=x^{3}y^{2}-xy+x^{2}y-10=0$

$F(x, y)=x\sin y+y\sin x-2=0$

$\dfrac{dy}{dx}=\dfrac{-(\sin y+y\cos x)}{x\cos y+\sin x}$

$F(x, y)=xe^{y}+ye^{x}-xy=0$

$F(x, y)=x^{1/3}+y^{1/3}-1=0$

$\dfrac{dy}{dx}=\dfrac{-y^{2/3}}{x^{2/3}}$

$F(x, y)=x^{2/3}+y^{2/3}-1=0$

In Problems 47–52, $z$ is a function of $x$ and $y$ . Find $\dfrac{\partial z}{\partial x}$ and $\dfrac{\partial z}{\partial y}$ .

$F(x,y,z)=xz+3yz^{2}+x^{2}y^{3}-5z=0$

$\dfrac{\partial z}{\partial x}=\dfrac{-(z+2xy^3)}{x+6yz-5}$ ; $\dfrac{\partial z}{\partial y}=\dfrac{-(3z^2+3x^2y^2)}{x+6yz-5}$

$F(x,y,z)=x^{2}z+y^{2}z+x^{3}y-10z=0$

$F(x,y,z)=\sin z+y\cos z+xyz-10=0$

$\dfrac{\partial z}{\partial x}=\dfrac{-yz}{\cos z-y\sin z+xy}$ ; $\dfrac{\partial z}{\partial y}=\dfrac{-(\cos z+xz)}{\cos z-y\sin z+xy}$

$F(x,y,z)=x\sin y-\cos z+x^{2}z=0$

$F(x,y,z)=xe^{yz}+ye^{xz}+xyz=0$

$\dfrac{\partial z}{\partial x}=\dfrac{-(e^{yz}+yze^{xz}+yz)}{xye^{yz}+xye^{xz}+xy}$ ; $\dfrac{\partial z}{\partial y}=\dfrac{-(xze^{yz}+e^{xz}+xz)}{xye^{yz}+xye^{xz}+xy}$

$F(x,y,z)=e^{yz}\ln x+ye^{xz}-yz=0$

In Problems 53 and 54, find $\dfrac{\partial w}{\partial x},$ $\dfrac{\partial w}{\partial y}$ , and $\dfrac{\partial w}{\partial z}$ .

$w=(2x+3y)^{4z}$

$\dfrac{\partial w}{\partial x}=8z(2x+3y)^{4z-1}$ ; $\dfrac{\partial w}{\partial y}=12z(2x+3y)^{4z-1}$ ; $\dfrac{\partial w}{\partial z}=4(2x+3y)^{4z}\ln(2x+3y)$

$w=(2x)^{3y+4z}$

Applications and Extensions

Ideal Gas Law One mole of a gas obeys the Ideal Gas Law $PV=20T$ , where $P$ is pressure, $V$ is volume, and $T$ is temperature. If the temperature $T$ of the gas is increasing at the rate of 5 $^{\circ}{\rm C}/{\rm s}$ and if, when the temperature is 80 $^{\circ}{\rm C}$ , the pressure $P$ is $10{\rm N}/{\rm m}^{2}$ and is decreasing at the rate of $2\dfrac{{\rm N}}{{\rm m}^{2}\cdot {\rm s}}$ , find the rate of change of the volume $V$ with respect to time.

$13.2$ m $^3/$ s

Melting Ice A block of ice of dimensions $l,$ $w,$ and $h$ is melting. When $l=3{\rm m}$ , $w=2{\rm m},$ $h=1{\rm m},$ these variables are changing so that $\dfrac{dl}{dt}=-1{\rm m}/{\rm h},$ $\dfrac{dw}{dt}=-1 {\rm m}/{\rm h}$ , and $\dfrac{dh}{dt}=-0.5{\rm m}/{\rm h}$ .
1. (a) What is the rate of change in the surface area of the block of ice?
2. (b) What is the rate of change in the volume of the block of ice?

Wave Equation The one-dimensional wave equation $\dfrac{ \partial ^{2}f}{\partial x^{2}}=\dfrac{1}{v^{2}}\dfrac{\partial ^{2}f}{ \partial t^{2}}$ describes a wave traveling with speed $v$ along the $x$ -axis. The function $f$ represents the displacement $x$ from the equilibrium of the wave at time $t$ .
1. Show that $z=f(x,t) =\sin (x+vt)$ satisfies the wave equation.
2. Show that $z=f(x,t) =e^{x-vt}$ satisfies the wave equation.
3. Show that $z=f(x,t) =\sin x+\sin (vt)$ does not satisfy the wave equation.
4. Show that any twice-differentiable function of the form $f(x+vt)$ is a solution of the wave equation.

(a) See Student Solutions Manual.
(b) See Student Solutions Manual.
(c) See Student Solutions Manual.
(d) See Student Solutions Manual.

Economics A toy manufacturer’s production function satisfies a Cobb–Douglas model, $Q( L,M) =400L^{0.3}M^{0.7}$ , where $Q$ is the output in thousands of units, $L$ is the labor in thousands of hours, and $M$ is the machine hours (in thousands). Suppose the labor hours are decreasing at a rate of $4000{\rm h}/{\rm yr}$ and the machine hours are increasing at a rate of $2000{\rm h}/{\rm yr}.$ Find the rate of change of production when
1. $L=19$ and $M=21$
2. $L=21$ and $M=20$

Related Rates Let $y=f(a,b),$ where $a=h(s,t)$ and $\ b=k(s,t)$ . Suppose when $s=1$ and $t=3$ , we know that $\frac{\partial h}{\partial s}=4\qquad \frac{\partial k}{\partial s} =-3\qquad \frac{\partial h}{\partial t}=1\qquad \frac{\partial k}{ \partial t}=-5$

Also, suppose $h(1,3)=6 \qquad k(1,3)=2 \qquad f_{a}( 6,2) =7 \qquad f_{b}( 6,2) =2$

What are $\dfrac{\partial y}{\partial s}$ and $\dfrac{\partial y}{\partial t}$ at the point $(1,3)$ ?

$\dfrac{\partial y}{\partial s}(1,3)=22$ ; $\dfrac{\partial y}{\partial t}(1,3)=-3$

Related Rates Let $z=f(x,y),$ where $x=g(s,t)$ and $\ y=h(s,t)$ . Suppose when $s=2$ and $t=-1$ , we know that $\frac{\partial x}{\partial s}=5\qquad \frac{\partial y}{\partial s} =2\qquad \frac{\partial x}{\partial t}=-3\qquad \frac{\partial y}{ \partial t}=-2$

Also, suppose $g(2,-1)=3 \quad\hspace{6pt} h(2,-1)=4\quad\hspace{6pt} f_{x}( 3,4) =12\quad\hspace{6pt} f_{y}( 3,4) =7$

What are $\dfrac{\partial z}{\partial s}$ and $\dfrac{\partial z}{\partial t}$ at the point $(2,-1)$ ?

If $z=f(x, y),$ where $x=g(u,v)$ and $y=h(u,v)$ , find expressions for $\dfrac{\partial ^{2}z}{\partial u^{2}}$ , $\dfrac{\partial ^{2}z}{\partial u~\partial v}$ , and $\dfrac{\partial ^{2}z}{\partial v^{2} }.$

$\begin{eqnarray*}\dfrac{\partial^2z}{\partial u^2}&=&\dfrac{\partial z}{\partial x}\dfrac{\partial^2x}{\partial u^2}+\dfrac{\partial z}{\partial y}\dfrac{\partial^2y}{\partial u^2}+\dfrac{\partial^2z}{\partial x^2}\left(\dfrac{\partial x}{\partial u}\right)^2+2\dfrac{\partial^2z}{\partial x\partial y}\left(\dfrac{\partial x}{\partial u}\right)\left(\dfrac{\partial y}{\partial u}\right)+\dfrac{\partial^2z}{\partial y^2}\left(\dfrac{\partial y}{\partial u}\right)^2\\ \dfrac{\partial^2z}{\partial u\partial v}&=&\dfrac{\partial z}{\partial x}\dfrac{\partial^2 x}{\partial u\partial v}+\dfrac{\partial z}{\partial y}\dfrac{\partial^2 y}{\partial u\partial v}+\dfrac{\partial^2z}{\partial x^2}\dfrac{\partial x}{\partial u}\dfrac{\partial x}{\partial v} + \dfrac{\partial^2 z}{\partial y^2}\dfrac{\partial y}{\partial u}\dfrac{\partial y}{\partial v}+\dfrac{\partial^2z}{\partial x\partial y}\left(\dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}+\dfrac{\partial y}{\partial v}\dfrac{\partial x}{\partial u} \right)\\ \dfrac{\partial^2z}{\partial v^2}&=&\dfrac{\partial z}{\partial x}\dfrac{\partial^2x}{\partial v^2}+\dfrac{\partial z}{\partial y}\dfrac{\partial^2y}{\partial v^2}+\dfrac{\partial^2z}{\partial x^2}\left(\dfrac{\partial x}{\partial v}\right)^2+2\dfrac{\partial^2z}{\partial x\partial y}\left(\dfrac{\partial x}{\partial v}\right)\left(\dfrac{\partial y}{\partial v}\right)+\dfrac{\partial^2z}{\partial y^2}\left(\dfrac{\partial y}{\partial v}\right)^2\end{eqnarray*}$

858

If $z=f(x, y)$ and $x=r\cos \theta$ , $y=r\sin \theta$ , show that $\left( \frac{\partial z}{\partial r}\right) ^{2}+\frac{1}{r^{2}}\left( \frac{ \partial z}{\partial \theta }\right) ^{2}=\left( \frac{\partial z}{\partial x }\right) ^{2}+\left( \frac{\partial z}{\partial y}\right) ^{2}$

If $z=f(x, y),$ where $x=u\cos \theta -v\sin \theta$ and $y=u\sin \theta +v\cos \theta$ , with $\theta$ a constant, show that $\left( \dfrac{\partial f}{\partial u}\right) ^{2}+\left( \dfrac{\partial f}{ \partial v}\right) ^{2}=\left( \dfrac{\partial f}{\partial x}\right) ^{2}+\left( \dfrac{\partial f}{\partial y}\right) ^{2}$ .

See Student Solutions Manual.

If $z=f(u-v,v-u)$ , show that $\dfrac{\partial z}{ \partial u}+\dfrac{\partial z}{\partial v}=0$ .

(Hint: Let $x=u-v$ and $y=v-u$ .)

If $z=vf(u^{2}-v^{2})$ , show that $v\dfrac{\partial z}{ \partial u}+u\dfrac{\partial z}{\partial v}=\dfrac{uz}{v}.$

See Student Solutions Manual.

If $w=f(u)$ and $u=\sqrt{x^{2}+y^{2}+z^{2}}$ , show that $\left( \dfrac{\partial w}{\partial x}\right) ^{2}+\left( \dfrac{\partial w}{ \partial y}\right) ^{2}+\left( \dfrac{\partial w}{\partial z}\right) ^{2}=\left( \dfrac{d w}{d u}\right) ^{2}$ .

If $z=f\left( \dfrac{x}{y}\right)$ , show that $x\dfrac{ \partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=0$ .

See Student Solutions Manual.

Show that if $z=f\left( \dfrac{u}{v}, \dfrac{v}{w}\right)$ , then $u\dfrac{\partial z}{\partial u}+v\dfrac{\partial z}{\partial v}+w \dfrac{\partial z}{\partial w}=0$ .

Suppose we denote the expression $\dfrac{\partial ^{2}}{ \partial x^{2}}+\dfrac{\partial ^{2}}{\partial y^{2}}$ by $\mathbf{\Delta }$ . If $z=f(x,y)$ , where $x=r\cos \theta$ and $y=r\sin \theta ,$ show that $\mathbf{\Delta }f=\dfrac{\partial ^{2}f}{\partial r^{2}}+\dfrac{1}{r}\left( \dfrac{\partial f}{\partial r}\right) +\dfrac{1}{r^{2}}\left( \dfrac{ \partial ^{2}f}{\partial \theta ^{2}}\right)$ .

See Student Solutions Manual.

Prove that if $F(x,y,z)=0$ is differentiable, then $\dfrac{\partial z}{\partial x}\cdot \dfrac{\partial x}{\partial y}\cdot \dfrac{\partial y}{\partial z}=-1.$

Challenge Problems

1. Suppose that $F(x,y)$ has continuous second-order partial derivatives and $F(x,y)=0$ defines $y$ as a function of $x$ implicitly. Show that $\frac{d^{2}y}{dx^{2}}=-\frac{F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}}{F_{y}^{3}}\qquad F_{y}\neq 0$
2. Use the result from (a) to find $\dfrac{d^{2}y}{dx^{2}}$ for $x^{3}+3xy-y^{3}=6$ .

(a) See Student Solutions Manual.
$\dfrac{d^2y}{dx^2}=-\dfrac{6x(3x-3y^2)^2-6(3x^2+3y)(3x-3y^2)-6y(3x^2+3y)^2}{(3x-3y^2)^3}$

$f(t,x)=\int_{0}^{x/(2\sqrt{\lambda t})}e^{-u^{2}}du$ . Show that $f_{t}=\lambda f_{xx}$ .

12.5 Assess Your UnderstandingPrinted Page 856

12.5 Assess Your Understanding
Printed Page 856