REVIEW EXERCISES

Printed Page 9999

In Problems 1–3, evaluate each function.

  1. \(f(x,y) =e^{x}\ln y\)

    1. (a) \(f( 1,1) \)
    2. (b) \(f(x+\Delta x, y)\)
    3. (c) \(f(x, y+\Delta y)\)

(a) 0

(b) ex+Δx ln y

(c) ex ln(y + Δy)

  1. \(f(x,y) =2x^{2}+6xy-y^{3}\)

    1. (a) \(f ( 1,1 ) \)
    2. (b) \(f(x+\Delta x, y)\)
    3. (c) \(f(x, y+\Delta y)\)

  1. \(f(x,y,z) =e^{x}\sin ^{-1}(y+2z) \)

    1. (a) \(f\left( \ln 3,\dfrac{1}{2},\dfrac{1}{4}\right) \)
    2. (b) \(f\left( 1,0,\dfrac{1}{4}\right) \)
    3. (c) \(f( 0,0,0) \)

(a)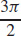

(b)

(c) 0

In Problems 4–7, find the domain of each function and graph the domain. Use a solid curve to indicate that the boundary is included and a dashed curve to indicate that the boundary is excluded.

  1. \(z=f(x,y)=\ln ( x^{2}-3y) \)

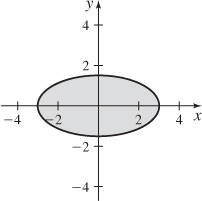
  1. \(z=f(x,y)=\sqrt{9-x^{2}-4y^{2}}\)

{(x, y) | x2 + 4y2 ≤ 9}

  1. \(z=f(x,y) =\dfrac{25xy}{\sqrt{5-y^{2}}}\)

  1. \(z=f(x,y) = \dfrac{(y-3x)^2}{x+2y} \)

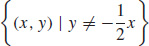
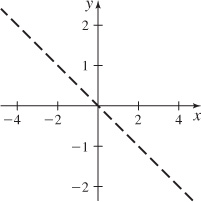
  1. Find the domain of \(w=f(x,y,z)=\dfrac{y^{2}+z^{2}}{x^{2}}.\)

  1. Find the domain of \(w=f(x,y,z)=e^{x+y}\ln z\).

{(x, y, z) | z > 0}

In Problems 10–13, graph each surface.

  1. \(z=f(x,y)=x-y+5\)

  1. \(z=f(x, y)=\sin x\)

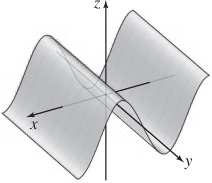
  1. \(z=f(x,y)=\ln x\)

  1. \(z=f(x,y)=e^{y}\)

  1. For \(z=f(x, y)=x^{2}-2y,\) graph the level curves corresponding to \(c=-4,\) \(-1,\) \(0,\) \(1,\) \(4.\)

  1. For \(z=f(x, y)=\sqrt{x^{2}+y^{2}},\) graph the level curves corresponding to \(c=0, 1, 4, 9.\)

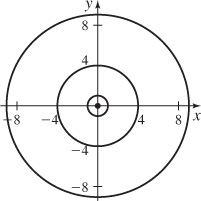
  1. For \(z=f(x,y) =e^{4x^{2}+y^{2}},\) graph the level curves corresponding to \(c=1,\) \(e,\) \(e^{4},\) \(e^{16}\).

  1. Describe the level surfaces associated with the function \( w=f(x, y, z)=4x^{2}+y^{2}+z^{2}\).

The level surfaces associated with the function w = 4x2 + y2 + z2 are ellipsoids and the point (0, 0, 0).

  1. Describe the level surfaces associated with the function \(w=f(x, y, z)=x+y+2z\).

  1. Find \(\lim\limits_{(x,y) \rightarrow \left( {\pi }/{2},0\right) }\dfrac{\sin x\cos y}{x}\).

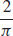
  1. Find \(\lim\limits_{(x, y)\rightarrow (1, 2)}\dfrac{4x^{2}+y^{2} }{2x+y}\).

  1. Let \(f(x, y)=\dfrac{3xy^{2}}{x^{2}+y^{4}}\).

    1. (a) Show that \(\lim\limits_{(x, y)\rightarrow (0, 0)}f(x, y)=0\) along the lines \(y=mx\).
    2. (b) Find \(\lim\limits_{(x, y)\rightarrow (0, 0)}f(x, y)\) along the parabola \( x=y^{2}\).
    3. (c) What can you conclude?

(a) See Student Solutions Manual.

(b)

(c) This limit does not exist.

860

  1. Show that \(\lim\limits_{(x, y, z)\rightarrow (0, 0, 0)}\dfrac{ 4xy}{x^{2}+y^{2}+z^{2}}\) does not exist.

  1. Determine where the function \(f(x,y) =2x^{2}y-y^{2}+3\) is continuous.

The function is continuous at all points (x, y) in the plane.

  1. Determine where the function \(R(x,y) =\dfrac{xy}{ x^{2}-y^{2}}\) is continuous.

    1. (a) Determine where the function \(f(x,y) =\tan ^{-1}\dfrac{1}{x^{2}+y^{2}}\) is continuous.
    2. (b) Find \(\lim\limits_{(x,y) \rightarrow ( 0,1) }\tan ^{-1}\dfrac{1}{x^{2}+y^{2}}.\)

(a) This function is continuous at all points (x, y) in the plane except the origin, (0, 0).

(b)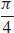

  1. Find \(f_{x}\) and \(f_{y}\) for \(z=f(x, y)=e^{x^{2}+y^{2}}\sin (xy)\).

  1. Find \(f_{x}\) and \(f_{y}\) for \(z=f(x, y)=\dfrac{x+y}{y}\).

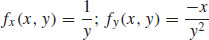
  1. Find \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{ \partial y}\) for \(z=f(x, y)=\sqrt{x-2y^{2}}\).

  1. Find \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{ \partial y}\) for \(z=f(x, y)=e^{x}\ln ( 5x+2y) \).

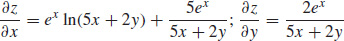
  1. For \(f(x, y)=\sqrt{x^{2}-y^{2}}\), find \(f_{x}(2,1)\) and \( f_{y}(2,-1)\).

  1. For \(F(x, y)=e^{x}\sin y\), find \(F_{x}\!\left( 0,\dfrac{\pi }{6} \right) \) and \(F_{y}\!\left( 0,\dfrac{\pi }{6}\right) \).

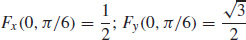
  1. Find symmetric equations for the tangent line to the curve of intersection of the ellipsoid \(\dfrac{x^{2}}{24}+\dfrac{y^{2}}{12}+\dfrac{ z^{2}}{6}=1\), and the plane \(y=1\), where \(x=4\) and \(z\) is positive.

  1. Find symmetric equations for the tangent line to the curve of intersection of the surface \(z=4x^{2}-y^{2}+7\):

    1. (a) With the plane \(y=-2\) at the point \((1,-2,7)\).
    2. (b) With the plane \(x=1\) at the point \((1,-2,7)\).

(a) \(y=-2\),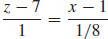

(b) x = 1,

  1. Boyle’s Law The volume \(V\) of a gas varies directly with the temperature \(T\) and inversely with the pressure \(P\).

    1. (a) Find the rate of change of the volume \(V\) with respect to the temperature \(T.\)
    2. (b) Find the rate of change of the volume \(V\) with respect to the pressure \(P.\)
    3. (c) If \(T\) and \(P\) are functions of \(t\), what is \(\dfrac{\partial V}{\partial t}\)?

In Problems 35 and 36, find the second-order partial derivatives \( f_{xx}, f_{xy}, f_{yx}\), and \(f_{yy}\).

  1. \(z=f(x,y) =( x+y^{2}) e^{3x}\)

fxx (x, y) = 6e3x + 9(x + y2)e3x; fxy(x, y) = 6ye3x; fyx (x, y) = 6ye3x; fyy(x, y) = 2e3x

  1. \(z=f(x,y) =\sec (xy) \)

In Problems 37–40, find \(f_{x}, f_{y}\), and \(f_{z}\).

  1. \(w=f(x,y,z)=e^{xyz}\)

fx = yzexyz; fy = xzexyz; fz = xyexyz

  1. \(w=f(x,y,z)=ze^{xy}\)

  1. \(f(x,y,z)=e^{x}\sin y+e^{y}\sin z\)

fx = ex sin y; fy = ex cos y + ey sin z; fz = ey cos z

  1. \(w=f(x,y,z)=z\tan ^{-1}\dfrac{y}{x}\)

  1. For the function \(z=x^{3}y^{2}-2xy^{4}+3x^{2}y^{3},\) show that \(x\dfrac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=5z\).

See Student Solutions Manual.

  1. Find the change \(\Delta z\) in \(z=f(x,y)=xy^{2}+2\) from \( (x_{0},y_{0})\) to \((x_{0}+\Delta x, y_{0}+\Delta y)\). Use the answer to calculate the change in \(z\) from \((1,0)\) to \((0.9,0.2)\).

  1. Show that the function \(z=f(x,y)=xy-5y^{2}\) is differentiable at any point \((x,y)\) in its domain by:

    1. (a) Finding \(\Delta z\).
    2. (b) Finding \(\eta _{1}\) and \(\eta _{2}\) so that \(\Delta z=f_{x}(x_{0},y_{0})\Delta x+ f_{y}(x_{0},y_{0})\Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y\).
    3. (c) Show that \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta_{1}=0\) and \(\lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{2}=0\).

(a) Δz = (y)Δx + (x − 10y)Δy + (Δy)Δx + (−5Δy)Δy

(b) η1 = Δy; η2 = −5Δy

(c) See Student Solutions Manual.

In Problems 44 and 45, find the differential \(dz\) of each function.

  1. \(z=x\sqrt{1+y^{2}}\)

  1. \(z=\sin ^{-1}\dfrac{x}{y}\), \(y>0\)

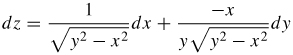
In Problems 46 and 47, find the differential \(dw\) of each function.

  1. \(w=ze^{xy}\)

  1. \(w=\ln (xyz)\)

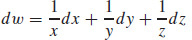
  1. Use differentials to estimate the change in \(z=x\sqrt{1+y^{2}}\) from \(( 4,0) \) to \(( 4.1,0.1) .\)

  1. Use differentials to estimate the change in \(z=\sin ^{-1}\dfrac{x}{y}\) from \(( 0,1)\) to \(( 0.1,1.1) .\)

\(\Delta z\) ≈ 0.1

  1. Use the differential of \(f(x,y)=y^{2}\cos x\) to find an approximate value of \(f(0.05,1.98)\). (Compare your answer with a calculator result.)

  1. Electricity The electrical resistance \(R\) of a wire is \(R=k \dfrac{L}{D^{2}}\) where \(L\) is the length of the wire, \(D\) is the diameter of the wire, and \(k\) is a constant. If \(L\) has a \(1\%\) error and \(D\) has a \(2\%\) error, what is the approximate maximum percentage error in the computation of \(R\)?

The approximate maximum percentage error is 5%.

  1. Find \(\dfrac{dz}{dt}\) if \(z=\sin (xy)-x\sin y,\) where \( x=e^{t} \) and \(y=te^{t}\).

  1. Find \(\dfrac{dw}{dt}\) if \(w=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{ x},\) where \(x=\dfrac{1}{t}\), \(y=\dfrac{1}{t^{2}}\), and \(z=\dfrac{1}{t^{3}}\).

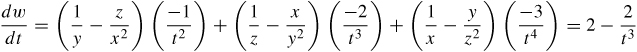
  1. Find \(\dfrac{\partial w}{\partial u}\) and \(\dfrac{\partial w}{ \partial v}\) if \(w=xy+yz-xz,\) where \(x=u+v\), \(y=uv\), and \(z=v\). Express each answer in terms of \(u\) and \(v.\)

  1. Find \(\dfrac{\partial u}{\partial r}\) and \(\dfrac{\partial u}{ \partial s}\) if \(u=\sqrt{x^{2}+y^{2}+z^{2}},\) where \(x=r\cos s\), \(y=r\sin s\) , and \(z=\sqrt{r^{2}+s^{2}}\). Express each answer in terms of \(r\) and \(s.\)

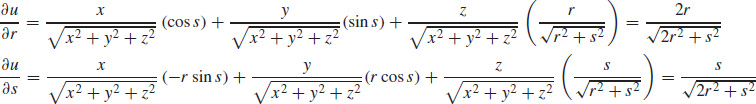
  1. Find \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{ \partial y}\) if \(z=f(x,y) \) is defined implicitly by \( F(x,y,z)=x^{2}+y^{2}-2xyz=0.\)

  1. Find \(\dfrac{\partial z}{\partial x}\) and \(\dfrac{\partial z}{ \partial y}\) if \(z=f(x,y) \) is defined implicitly by \( F(x,y,z)=2x\sin y+2y\sin x+2xyz=0.\)

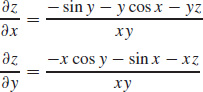
  1. If \(z=uf( u^{2}+v^{2}) ,\) show that \(2v\dfrac{ \partial z}{\partial u}-2u\dfrac{\partial z}{\partial v}=\dfrac{2vz}{u}.\)