12.3 Assess Your UnderstandingPrinted Page 837
Concepts and Vocabulary
True or False To find the partial derivative fy(x,y), differentiate f with respect to x while treating y as if it were a constant.
False
Multiple Choice The partial derivative fx(x0,y0) equals the slope of the tangent line to the curve of intersection of the surface z=f(x,y) and the plane [(a) x=x0, (b) y=y0, (c) z=z0, (d) x+y+z=0] at the point (x0,y0,f(x0,y0)) on the surface.
(b)
True or False fx(x,y) equals the rate of change of f in the direction of the positive x-axis.
True
The two second-order partial derivatives ∂2z∂x∂y and ∂2z∂y∂x are called ____ partials.
Mixed
True or False If f(x,y)=xcosy, then fx(x,y)= fy(x,y).
False
For a function w=f(x,y,z) of three variables, to find the partial derivative fy(x,y,z), treat the variables ____ and ____ as constants, and differentiate f with respect to ____.
x; z; y
Skill Building
In Problems 7–14, find fx(x,y) and fy(x,y).
f(x,y)=x2y+6y2
fx(x,y)=2xy; fy(x,y)=x2+12y
f(x,y)=3x2+6xy3
f(x,y)=x−yx+y
fx(x,y)=2y(x+y)2; fy(x,y)=−2x(x+y)2
f(x,y)=x+yy2
f(x,y)=eycosx+exsiny
fx(x,y)=−eysinx+exsiny; fy(x,y)=eycosx+excosy
f(x,y)=x2cosy+y2sinx
f(x,y)=x2exy
fx(x,y)=2xexy+x2yexy; fy(x,y)=x3exy
f(x,y)=cos(x2y3)
In Problems 15–20, find ∂z∂x and ∂z∂y.
z=f(x,y)=tan−1yx
∂z∂x=−yx2+y2; ∂z∂y=xx2+y2
z=f(x,y)=sin2(2xy)
z=f(x,y)=sin(ex2y)
∂z∂x=2xyex2ycos(ex2y); ∂z∂y=x2ex2ycos(ex2y)
z=f(x,y)=sin[ln(x2+y2)]
z=f(x,y)=e(x2+y2)1.2
∂z∂x=2.4x(x2+y2)0.2e(x2+y2)1.2; ∂z∂y=2.4y(x2+y2)0.2e(x2+y2)1.2
z=f(x,y)=ln√x2+y2
In Problems 21–26, find the second-order partial derivatives fxx,fxy,fyx, and fyy. Check to verify that fxy=fyx.
f(x,y)=6x2−8xy+9y2
fxx=12; fxy=−8; fyx=−8; fyy=18
f(x,y)=(2x+3y)(3x−2y)
f(x,y)=ln(x3+y2)
fxx=−3x(x3−2y2)(x3+y2)2; fxy=−6x2y(x3+y2)2; fyx=−6x2y(x3+y2)2; fyy=2(x3−y2)(x3+y2)2
f(x,y)=e2x+3y
f(x,y)=cos(x2y3)
fxx=−4x2y6cos(x2y3)−2y3sin(x2y3); fxy=−6x3y5cos(x2y3)−6xy2sin(x2y3); fyx=−6x3y5cos(x2y3)−6xy2sin(x2y3); fyy=−9x4y4cos(x2y3)−6x2ysin(x2y3)
f(x,y)=sin2(xy)
In Problems 27–34, find fx(x,y,z), fy(x,y,z), and fz(x,y,z).
f(x,y,z)=xy+yz+xz
fx(x,y,z)=y+z; fy(x,y,z)=x+z; fz(x,y,z)=x+y
f(x,y,z)=xey+yez+zex
f(x,y,z)=xysinz−yzsinx
fx(x,y,z)=ysinz−yzcosx; fy(x,y,z)=xsinz−zsinx; fz(x,y,z)=xycosz−ysinx
f(x,y,z)=1√x2+y2+z2
f(x,y,z)=ztan−1yx
fx(x,y,z)=−yzx2+y2; fy(x,y,z)=xzx2+y2; fz(x,y,z)=tan−1(yx)
f(x,y,z)=tan−1xyz
838
f(x,y,z)=sin[ln(x2+y2+z2)]
fx(x,y,z)=2xcos[ln(x2+y2+z2)]x2+y2+z2; fy(x,y,z)=2ycos[ln(x2+y2+z2)]x2+y2+z2; fz(x,y,z)=2zcos[ln(x2+y2+z2)]x2+y2+z2
f(x,y,z)=ex2+y2lnz
In Problems 35 and 36, use the definition of a partial derivative to find fx(0, 0) and fy(0, 0).
f(x,y)={x3+y3x2+y2if(x,y)≠(0,0)0if(x,y)=(0,0)
fx(0,0)=1; fy(0,0)=1
f(x,y)={x2y2x2+4y3if(x,y)≠(0,0)0if(x,y)=(0,0)
In Problems 37–42, find symmetric equations of the tangent line to the curve of intersection of each surface with the given plane at the indicated point.
z=x2+y2 and y=2 at (1,2,5)
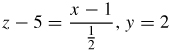
z=x2−y2 and x=3 at (3,1,8)
z=√1−x2−y2 and x=0 at (0,12,√32)
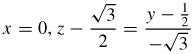
z=√16−x2−y2 and y=2 at (√3,2,3)
z=√x2+y2 and x=4 at (4,2,2√5)
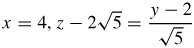
z=exlny and y=e at (0,e,1)
Find the rate of change of z=ln√x2+y2 at (3,4,ln5),
- (a) In the direction of the positive x-axis.
- (b) In the direction of the positive y-axis.
- (a) 325
- (b) 425
Find the rate of change of z=eysinx at (π3,0,√32),
- (a) In the direction of the positive x-axis.
- (b) In the direction of the positive y-axis.
Applications and Extensions
Temperature Distribution The temperature distribution T (in degrees Celsius) of a heated plate at a point (x,y) in the xy-plane is modeled by T=T(x,y)=(100ln2)ln(x2+y2)1≤x2+y2≤9
- (a) Show that T=0 ∘C on the circle x2+y2=1, and T=200 ∘C on the circle x2+y2=4.
- (b) Find the rate of change of T in the direction of the positive x-axis at the point (1,2) and at the point (2,1). Describe the rate of change.
- (c) Find the rate of change of T in the direction of the positive y-axis at the point (2,0) and at the point (0,2). Describe the rate of change.
- (a) See Student Solutions Manual.
- (b) 40ln2≈57.708; 80ln2≈115.416. For every unit increase in the direction of the positive x-axis from the point (1,2), there is an increase in the temperature of the plate of approximately 58∘C, and from (2,1) the increase is approximately 115∘C.
- (c) 0; 100ln2≈144.270. For every unit increase in the direction of the positive y-axis from the point (2,0), there is approximately no increase in the temperature of the plate, and from (0,2) the increase is approximately 144∘C.
Temperature Distribution The temperature distribution (in degrees Celsius) of a heated plate at a point (x,y) in the xy-plane is modeled by T=T(x,y)=100√x2+y2, 1≤x2+y2≤9.
- (a) Show that T=100∘C on the circle x2+y2=1, and T=50∘C on the circle x2+y2=4.
- (b) Find the rate of change of T in the direction of the positive x -axis at the point (1,0) and at the point (0,1). Describe the rate of change.
- (c) Find the rate of change of T in the direction of the positive y-axis at the point (2,0) and at the point (0,2). Describe the rate of change.
Thermodynamics The Ideal Gas Law PV=nrT is used to describe the relationship between pressure P, volume V, and temperature T of a confined gas, where n is the number of moles of the gas and r is the universal gas constant. Show that ∂V∂T⋅∂T∂P⋅∂P∂V=−1
See Student Solutions Manual.
Thermodynamics The volume V of a fixed amount of gas varies directly with the temperature T and inversely with the pressure P. That is, V=kTP, where k>0 is a constant.
- (a) Find ∂V∂T and ∂V∂P.
- (b) Show that T∂V∂T+P∂V∂P=0.
Economics The data used to develop the Cobb–Douglas productivity model included capital input K and labor input L for each year during the period 1899–1922. Using the model P=aKbL1−b and multiple regression techniques, Cobb and Douglas determined that manufacturing productivity was represented by the function P=1.014651K0.254124L0.745876≈1.01K0.25L0.75
- (a) Find the marginal productivity with respect to capital input and the marginal productivity with respect to labor input in 1900 when K=107 and L=105.
- (b) Find the marginal productivity with respect to capital input and the marginal productivity with respect to labor input in 1920 when K=407 and L=193.
- (c) Compare the answers. What do you conclude about the change in manufacturing productivity in the United States during the 20-year period?
- (a) ∂P∂K≈0.249; ∂P∂L≈0.761
- (b) ∂P∂K≈0.144; ∂P∂L≈0.913
- (c) Answers will vary.
Economics The function z=f(x,y,r)=1+(1−x)y1+r−1
describes the net gain or loss of money invested, where x= annual marginal tax rate, y= annual effective yield on an investment, and r= annual inflation rate.
- (a) Find the annual net gain or loss if money is invested at an effective yield of 4% when the marginal tax rate is 25% and the inflation rate is 5%; that is, find f(0.25,0.04,0.05).
- (b) Find the rate of change of gain (or loss) of money with respect to the marginal tax rate when the effective yield is 4% and the inflation rate is 5%.
- (c) Find the rate of change of gain (or loss) of money with respect to the effective yield when the marginal tax rate is 25% and the inflation rate is 5%.
- (d) Find the rate of change of gain (or loss) of money with respect to the inflation rate when the marginal tax rate is 25% and the effective yield is 4%. Use r=5%
839
Economics Let w=2x1/2y1/3z1/6 be a production function that depends on three inputs: x, y, and z. Find the marginal productivity with respect to x, the marginal productivity with respect to y, and the marginal productivity with respect to z.
∂w∂x=y1/3z1/6x1/2; ∂w∂y=2x1/2z1/63y2/3; ∂w∂z=x1/2y1/33z5/6
Speed of Sound The speed v of sound in a gas depends on the pressure p and density d of the gas and is modeled by the formula v(p,d)=k√pd, where k is some constant. Find the rate of change of speed with respect to p and with respect to d.
Vibrating Strings Suppose a vibrating string is governed by the equation f(x,t)=2cos(5t)sinx, where x is the horizontal distance of a point on the string, t is time, and f(x,t) is the displacement. Show that ∂2f∂t2=25∂2f∂x2 at all points (x,t).
See Student Solutions Manual.
Temperature Distribution Suppose a thin metal rod extends along the x-axis from x=0 to x=20, and for each x, where 0≤x≤20, the temperature T of the rod at time t≥0 and position x is T(t,x)=40e−λtsinπx20, where λ>0 is a constant.
- (a) Show that Tt=−λT, Txx=−π2400T, and Tt=1k2Txx for some k.
- (b)
 Graph the initial temperature distribution, y=T(0,x), where 0≤x≤20.
Graph the initial temperature distribution, y=T(0,x), where 0≤x≤20.
Find ∂x∂r,∂x∂θ,∂y∂r, and ∂y∂θ if x=rcosθ and y=rsinθ.
∂x∂r=cosθ; ∂x∂θ=−rsinθ; ∂y∂r=sinθ; ∂y∂θ=rcosθ
Find ∂r∂x,∂θ∂x,∂r∂y, and ∂θ∂y
if r=√x2+y2 and θ=tan−1yx, x≠0.

- (a) Graph f(x,y)=12x2+13y2 and the plane y=1.
- (b) Find symmetric equations of the tangent line to the curve of intersection of the surface and the plane at the point (2,1,73).
- (a)
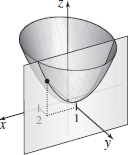
- (b)
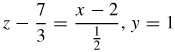

- (a) Graph f(x,y)=5√x2+y2+1 and the plane x=1.
- (b) Find symmetric equations of the tangent line to the curve of intersection of the surface and the plane at the point (1,−2,5√66).
Show that ∂u∂x=∂v∂y and ∂u∂y=−∂v∂x for u=excosy and v=exsiny.
See Student Solutions Manual.
Show that ∂u∂x=∂v∂y and ∂u∂y=−∂v∂x for u=ln√x2+y2 and v=tan−1yx.
If u=x2+4y2, show that x∂u∂x+y∂u∂y=2u.
See Student Solutions Manual.
If u=xy2, show that x∂u∂x+y∂u∂y=3u.
If w=x2+y2−3yz, show that x∂w∂x+y∂w∂y+z∂w∂z=2w.
See Student Solutions Manual.
If w=xz+y2yz, show that x∂w∂x+y∂w∂y+z∂w∂z=0.
If z=cos(x+y)+cos(x−y), show that ∂2z∂x2−∂2z∂y2=0.
See Student Solutions Manual.
If z=sin(x−y)+ln(x+y), show that ∂2z∂x2=∂2z∂y2.
Show that u=e−α2tsin(αx) satisfies the equation ∂u∂t=∂2u∂x2 for all values of the constant α.
See Student Solutions Manual.
Laplace’s Equation A function z=f(x,y) that obeys the partial differential equation ∂2z∂x2+∂2z∂y2=0 is called a harmonic function.* In Problems 68–71, show that each function is a harmonic function.
z=ln√x2+y2
z=eaxsin(ay)
See Student Solutions Manual.
z=tan−1yx
z=eaxcos(ay)
See Student Solutions Manual.
Harmonic Functions Suppose u(x,y) and v(x,y) have continuous second-order partial derivatives, ux=vy and uy=−vx. Show that u and v are harmonic functions.
Harmonic Functions If u=ztan−1xy, show that ∂2u∂x2+∂2u∂y2+∂2u∂z2=0.
See Student Solutions Manual.
Harmonic Functions Show that f(x,y,z)=(x2+y2+z2)−1/2 satisfies the three-dimensional Laplace equation fxx+fyy+fzz=0
Let f(x,y)={xy3x2+y2if(x,y)≠(0,0)0if(x,y)=(0,0)
- (a) Find fx and fy. [Hint: fx and fy, where (x,y)≠(0,0), can be found using derivative formulas. To find fx(0,0) and fy(0,0), use the definition of a partial derivative.]
- (b) Show that fxy(0,0)≠fyx(0,0).
- (a) fx(x,y)={−y3(x2−y2)(x2+y2)2(x,y)≠(0,0)0(x,y)=(0,0) fy(x,y)={xy2(3x2+y2)(x2+y2)2(x,y)≠(0,0)0(x,y)=(0,0)
- (b) See Student Solutions Manual.
Let f(x,y)={xy(x2−y2)x2+y2if(x,y)≠(0,0)0if(x,y)=(0,0)
Show that:
- (a) fx(0,y)=−y
- (b) fy(x,0)=x
- (c) fxy(0,0)=−1
- (d) fyx(0,0)=1
If you are told that f is a function of two variables whose partial derivatives are fx(x,y)=3x−y and fy(x,y)=x−3y, should you believe it? Explain.
No; answers will vary.
*Laplace’s equation is important in many applications including fluid dynamics, heat, elasticity, and electricity.
840
Show that there is no function z=f(x,y) for which fx(x,y)=2x−y and fy(x,y)=x−2y.
Use the definition of a partial derivative to show that the function z=√x2+y2 does not have partial derivatives at (0,0). By discussing the graph of the function, give a geometric reason why this should be so.
See Student Solutions Manual.
If z=f(x,y)=4x2+9y2−12, interpret fx(1,−13) and fy(1,−13) geometrically.
Show that xfx+yfy+zfz=0 for f(x,y,z)=ex/y+ey/z+ez/x.
See Student Solutions Manual.
Find a in terms of b and c so that f(t,x,y)=eatsin(bx)cos(cy) satisfies ft=fxx+fyy.
Wave Equation Show that f(x,t)=cos(x+ct) satisfies the one-dimensional wave equation ftt=c2fxx, where c is a constant.
See Student Solutions Manual.
Find fx and fy if f(x,y)=∫yxln(cos√t) dt.
Find ∂a∂b, ∂a∂c, and ∂a∂A for the Law of Cosines: a2=b2+c2−2bccosA.
∂a∂b=b−ccosA√b2+c2−2bccosA; ∂a∂c=c−bcosA√b2+c2−2bccosA; ∂a∂A=bcsinA√b2+c2−2bccosA
If x=rcosθ and y=rsinθ, show that |∂x∂r∂x∂θ∂y∂r∂y∂θ|=rand|∂r∂x∂r∂y∂θ∂x∂θ∂y|=1r
Challenge Problems
In Problems 87 and 88, find fx and fy.
f(x,y)=xy
fx=xy−1y; fy=xylnx
f(x,y)=x2x+3y
In Problems 89–92, find fx,fy, and fz.
f(x,y,z)=xy+z
fx=(y+z)xy+zx; fy=xy+zlnx; fz=xy+zlnx
f(x,y,z)=xyz
f(x,y,z)=(x+y)z
fx=(x+y)z−1z; fy=(x+y)z−1z; fz=(x+y)zln(x+y)
f(x,y,z)=(xy)z
Find fx and fy at (0,0) if f(x,y)={e−1/(x2+y2)if(x,y)≠(0,0)0if(x,y)=(0,0)
fx(0,0)=0;fy(0,0)=0
Find fx, fy, fxx, fyy, and fxy for f(x,y)=(xy)xy. What is the domain of f?
Show that the following function has first partial derivatives at all points in the plane: f(x,y)={x3−y3x2+y2if(x,y)≠(0,0)0if(x,y)=(0,0)
See Student Solutions Manual.
Laplace’s Equation in Polar Coordinates Show that the function f(r,θ)=rnsin(nθ) satisfies the Laplace equation frr+1rfr+1r2fθθ=0
Let u=rmcos(mθ). Show that ∂2u∂r2+1r2(∂2u∂θ2)+1r(∂u∂r)=0forallm.
See Student Solutions Manual.
- (a) Find symmetric equations of the tangent lines at (x0,y0,f(x0,y0)) to the curve of intersection of z=f(x,y) and y=y0, and the curve of intersection of z=f(x,y) and x=x0.
- (b) Write an equation of the plane determined by these two lines.
- (c) What is the geometric relationship of this plane to the surface z=f(x,y)?
Consider two coordinate systems as given in the figure.
- (a) Let f(x,y)=3x2+4y3. Find fx(1,6) and fy(1,6).
- (b) Let (a,b) be the x′y′-coordinates of (1,6). Let ˉf(x′,y′)=f(x,y). Find ˉfx′(a,b) and ˉfy′(a,b).
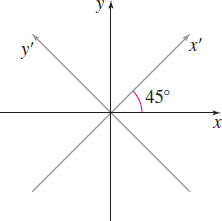
- (a) fx(1,6)=6; fy(1,6)=432
- (b) ˉfx′(a,b)=219√2; ˉfy′(a,b)=213√2
