Question

True or False If \(z=x\sin y,\) then the change in \(z\) from \(\left( 0.9,0\right)\) to \(\left( 1,\dfrac{\pi }{4}\right)\) is \(\Delta z=\sin \dfrac{\pi }{4}-0.9\;\sin\;0=\dfrac{\sqrt{2}}{2}.\)

Question

True or False If \(f_{x}(x,y) =-\dfrac{y^{2}}{1-x}\) and \(f_{y}(x,y) = 2y\;\ln\;(1-x) ,\) then \(f\) is differentiable at \(( 0,2)\).

Question

True or False Let \(z=f(x,y) =e^{x}\cos\;y\). Then the differential \(dz\) of \(z\) at \(\left( 0,\dfrac{\pi }{2}\right)\) is \(dz=-dy.\)

Question

True or False If the partial derivatives of a function \(z=f(x,y)\) are \(f_{x}(x,y) =2x+y\) and \(f_{y}(x,y) =x,\) then \(f\) is continuous.

Question

True or False If the partial derivatives of a function \(z=f(x,y)\) are \(f_{x}(x,y) =2x+y\) and \(f_{y}(x,y) =x,\) then \(f\) is differentiable.

Question

True or False If \(w=f(x,y,z) =e^{xyz}\), then \(dw=yze^{x}dx+xze^{y}dy+xye^{z}dz.\)

Question

\(z=x^{2}+y^{2}\) from \((1,3)\) to \((1.1,3.2)\)

Question

\(z=2x^{2}+xy-y^{2}\) from \((2,-1)\) to \((2.1,-1.1)\)

Question

\(z=e^{x}\ln (xy)\) from \((1, 2)\) to \((0.9, 2.1)\)

Question

\(z=\dfrac{xy}{x+y}\) from \((-1, 2)\) to \((-0.9, 1.9)\)

Question

\(z=x^{2}+y^{2}\)

Question

\(z=2x^{2}+xy-y^{2}\)

Question

\(z=x\;\sin y+y\;\sin x\)

Question

\(z=e^{x}\;\cos\;y+e^{-x}\;\sin\;y\)

Question

\(z=\tan ^{-1}\dfrac{y}{x}\)

Question

\(z=x\;\tan ^{-1}y\)

Question

\(z=\ln \dfrac{y}{x}\)

Question

\(z=\ln (x^{2}+y^{2})\)

Question

\(z=e^{xy}\)

Question

\(z=e^{x^{2}+y}\)

Question

\(z=x^{2}y+e^{y^{2}}\)

Question

\(z=xy^{3}-\;\ln\;x^{2}\)

Question

\(w=xe^{yz}+ye^{xz}+ze^{xy}\)

Question

\(w=x^{2}y+y^{2}z+z^{2}x\)

Question

\(w=\ln (x^{2}+y^{2}+z^{2})\)

Question

\(w=\ln (xy) +\ln (xz) +\ln(yz)\)

Question

\(w=xyz\)

Question

\(w=\dfrac{xyz}{x+y+z}\)

Question

\(z=f(x,y)=xy^{2}-2xy\)

Question

\(z=f(x,y)=3x^{2}+y^{2}\)

Question

\(z=f(x,y)=\dfrac{y}{x}\)

Question

\(z=f(x,y)=\dfrac{2x}{y}\)

Question

1. Use a differential to approximate the change in \(z=x^{2}+y^{2}\) from \((1, 3)\) to \((1.1, 3.2).\)
2. Compare the answer in (a) with the actual change in \(z\) found in Problem 7.

Question

1. Use a differential to approximate the change in \(z=2x^{2}+xy-y^{2}\) from \((2,-1)\) to \((2.1,-1.1).\)
2. Compare the answer in (a) with the actual change in \(z\) found in Problem 8.

Question

1. Use a differential to approximate the change in \(z=e^{x}\ln (xy)\) from \((1, 2)\) to \((0.9, 2.1).\)
2. Compare the answer in (a) with the actual change in \(z\) found in Problem 9.

Question

1. Use a differential to approximate the change in \(z=\dfrac{xy}{x+y}\) from \((-1, 2)\) to \((-0.9, 1.9).\)
2. Compare the answer in (a) with the actual change in \(z\) found in Problem 10.

Question

Area of a Triangle  Approximate the increase in the area of a triangle if its base is increased from \(2\) to \(2.05\;\rm{cm}\) and its height is increased from \(5\) to \(5.1\;\rm{cm}\).

Question

Area of a Triangle Approximate the change in the area of a triangle if the base is increased from \(5\) to \(5.1\;\rm{cm}\) and the height is decreased from \(10\) to \(9.8\;\rm{cm}\).

Question

Volume and Surface Area of a Cylinder

1. Use a differential to approximate the change in the volume of a right circular cylinder if the height changes from \(2\) to \(2.1\;\rm{cm}\) and the radius changes from \(0.5\) to \(0.49\;\rm{cm}\).
2. Approximate the change in the surface area of the cylinder. Assume that the cylinder is closed on the top and on the bottom.

848

Question

Electricity  In a parallel circuit, the total resistance \(R\) due to two sources of resistance \(R_{1}\) and \(R_{2}\) is given by \(\dfrac{1}{R}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\). If \(R_{1}=50~\rm{\Omega}\) with a possible error of \(1.2\%\) and \(R_{2}=75~\rm{\Omega}\) with a possible error of \(1\%\), what is the approximate maximum variation in the total resistance?

Question

Specific Gravity The specific gravity of an object is defined as \(s=\dfrac{a}{a-w}\), where \(a\) is the weight of the object in the air and \(w\) is its weight in water. If \(a\) is found to be \(6\;\rm{lb}\) with a possible error of \(1\%\) and \(w\) is \(5\;\rm{lb}\) with a possible error of \(2\%\), what is the approximate maximum variation in the specific gravity?

Question

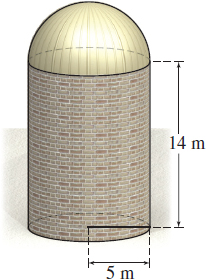
Volume A grain silo consists of a hemisphere mounted on a cylinder of the same radius (see the figure). The height and radius of the cylinder are measured as \(14\;\rm{m}\) and \(5\rm{m}\), respectively. However, the device used to make this measurement was found to be in error by \(1\%\). What is the approximate maximum variation in the volume of the silo?

Question

Snell’s Law The index of refraction is defined as \(\mu =\dfrac{\sin i}{\sin r}\), where \(i\) is the angle of incidence and \(r\) is the angle of refraction. If \(i=30{^\circ}\)and \(r=60{^\circ}\), and each measurement is subject to a possible error of \(2\%\), what is the approximate maximum relative error for \(\mu\)?

Question

Ideal Gas Law The equation \(PV=kT\), where \(k\) is a constant, relates the pressure \(P\), volume \(V\), and temperature \(T\) of one mole of an ideal gas. If \(P=0.1\rm{g}/\rm{\!mm}^{2}\), \(V=12\rm{mm}^{3}\), and \(T=32\ ^{\circ}{\rm C}\), approximate the change in \(P\) if \(V\) and \(T\) change to \(15\rm{mm}^{3}\) and 29 \(^{\circ}{\rm C}\), respectively.

Question

Determining Density In a laboratory experiment, the average density \(\rho\) of a spherical object is computed by measuring the mass \(m\) and diameter \(d\) of the sphere. In all empirical measurements, there is error caused by the inaccuracy of the tool, the scientist, or both. Suppose the experimental measurements are \(m=24.0\rm{g}\pm 1\%\) and \(d=1.5\rm{cm}\pm 5.0\%\).

1. Find the approximate maximum error in the computed density.
2. Find the approximate maximum percentage error in the computed density.

Question

Geometry Two sides, \(b\) and \(c,\) and the included angle \(\alpha\) of a triangle are measured by a ruler (for sides) and protractor (for angles), which are subject to errors of \(2\%\) and \(3\%\), respectively. The area of the triangle is then computed from the formula \[ A=\dfrac{1}{2}bc\sin \alpha \]

1. Show that \(\dfrac{dA}{A}=\dfrac{db}{b}+\dfrac{dc}{c}+\cot \alpha\,d\alpha\).
2. If \(\alpha =\dfrac{\pi }{4}\), what is the approximate maximum relative variation in the computation of \(A\)?

Question

1. Find the partial derivatives \(f_{x}\) and \(f_{y}\) of the function \(f(x,y) =\sqrt{x^{2}+y^{2}-2x -6y+10}.\)
2. Determine where the partial derivatives are continuous.
3. Graph the surface \(f(x,y) =\sqrt{x^{2}+y^{2}-2x -6y+10}.\)
4. Use the graph to give a geometric interpretation to the discontinuity found in (b).

Question

If \(x=r\;\cos\;\theta\) and \(y=r\;\sin\;\theta\), show that \(x\;dy-y\;dx=r^{2}d\;\theta\).

Question

Let \(f(x,y)=\left\{\begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{2xy}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0)\\ 0 & \hbox{if} & (x,y)=(0,0) \end{array} \right.\).

Question

Let \(f(x, y)=\left\{\begin{array}{@{}c@{\quad}c@{\quad}c}\dfrac{xy(1+y^{2})}{x^{2}+y^{2}} & \hbox{if } & (x,y)\neq (0,0)\\ 0 & \hbox{if } & (x,y)=(0,0) \end{array}\right.\).

Question

Let \(f(x, y)=\left\{\begin{array}{@{}c@{\quad}c@{\quad}c}\dfrac{xy-1}{x^{2}+y^{2}-2} & \hbox{if} & x^{2}+y^{2}\neq 2\\ \dfrac{1}{2} & \hbox{if} & x^{2}+y^{2}=2 \end{array}\right.\).

Show that \(f_{x}(1,1)\) and \(f_{y}(1,1)\) each exist, but \(f\) is not differentiable at \((1,1)\).

Question

Let \(f(x, y)=\left\{\begin{array}{@{}c@{\quad}c@{\quad}c}\dfrac{x^{2}y^{2}}{x^{4}+y^{4}} & \hbox{if} & (x, y)\neq (0, 0)\\ 0 & \hbox{if} & (x, y)=(0, 0) \end{array}\right.\).

Show that \(f_{x}(0,0)\) and \(f_{y}(0,0)\) each exist, but \(f\) is not differentiable at \((0,0)\).

Question

Electrical Resistance The electrical resistance \(R\) of a wire is given by \(R=\dfrac{\rho L}{A},\) where \(L\) is the length of the wire, \(A\) is its cross-sectional area, and \(\rho\) is the resistivity of the wire. If the temperature of the wire increases by \(\Delta T\), the wire expands so \(L\) and \(A\) change. The resistivity \(\rho\) also changes. The change in the length \(L\) is given by \(\Delta L=L_{0}\alpha \Delta T,\) the change in the radius \(r\) is \(\Delta r=r_0\alpha \Delta T\), and the change in the resistivity \(\rho\) is \(\Delta \rho =\rho _{0}K\Delta T\), where \(\alpha\) and \(K\) are constants that depend on the material being heated, \(L_{0}\) is the initial length, \(r_0\) is the initial radius, and \(\rho _{0}\) is the initial resistivity.

A copper wire with a circular cross-sectional area \(A\) has a resistance \(R\) of \(0.50\rm{\Omega}\) at \(0{}^{\circ}{\rm C}\). But suppose the temperature of the wire increases to \(40\rm{{}^{\circ}{\rm C}}\) from the heat generated by the current passing through the wire. For copper, \(\alpha =5.1\times 10^{-5}\left(\! \rm{{}^{\circ}{\rm C}}\right)^{-1}\) and \(K=3.93\times 10^{-3}\left( \rm{{}^{\circ}{\rm C}}\right) ^{-1}\).

1. Find the resistance \(R\) of the wire at \(40\rm{{}^{\circ}{\rm C}}\).
2. Find the percent change in the resistance \(R\) of the wire caused by the change in temperature.
3. Which effect contributes more to the change in resistance: the expansion of the wire or the increase in the resistivity?

Question

1. Find the differential of \(f(x,y,z)=x^{y^{z}}\).
2. Find the differential of \(g(x,y,z)=(x^{y})^{z}\).