14.5 Assess Your UnderstandingPrinted Page 939
Concepts and Vocabulary
True or False Suppose R is a closed, rectangular region in the xy-plane with sides of length Δx and Δy. If the perimeter of R is projected upward parallel to the z -axis, the result is a cylinder. If Sp is the area cut from the plane z=ax+by+c by this cylinder, then Sp=√a2+b2+1ΔxΔy.
True
True or False Suppose z=f(x,y) is a function of two variables defined on a closed, bounded region R. If fx and fy are continuous on R, then the area S of the part of the surface that lies over R is given by S=∬.
False
Skill Building
Find the surface area of the part of the plane 2x+2y+z=6 that lies above the region in the xy-plane bounded by x^{2}+y^{2}=4, the x-axis, and the y-axis, as shown in the figure.

S = 3\pi
940
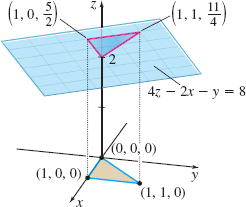
Find the surface area of the part of the plane 4z-2x-y=8 that lies over the region enclosed by the triangle with vertices (0,0,0), (1,0,0), and ( 1,1,0), as shown in the figure.
In Problems 5–16, find the surface area described.
The part of the surface z=f(x,y) =\sqrt{ 9-x^{2}} that lies above the rectangle enclosed by the lines x=0, x=2, y=-1, y=4
S = 15\;\sin^{-1} \left( \dfrac{2}{3} \right)
The part of the surface z=f(x,y) =\sqrt{8-y^{2}} that lies above the rectangle enclosed by the lines x=0, x=5, y=0, y=2
The part of the surface z=\dfrac{2}{3}( x^{3/2}+y^{3/2}) that lies above the triangle enclosed by the lines x=0, y=0, and 2x+3y=6
S = \dfrac{52}{3} - \dfrac{36 \sqrt{3}}5
The part of the surface z=\dfrac{2}{3}(x^{3/2}+y^{3/2}) that lies above the triangle enclosed by x=0, y=0, and 3x+y=3
The part of the paraboloid z=4-x^{2}-y^{2} that lies above the xy-plane
S = \dfrac{\pi}6 \big(17 \sqrt{17} - 1\big)
The part of the cylinder z=\sqrt{a^{2}-x^{2}} that lies above the square defined by -\dfrac{1}{2}a\leq x\leq \dfrac{1}{2}a and -\dfrac{1 }{2}a\leq y\leq \dfrac{1}{2}a, a\gt 0
The part of the cone z=\sqrt{x^{2}+y^{2}} that lies inside the cylinder x^{2}+y^{2}=2x
S = \sqrt{2} \pi
The part of the sphere x^{2}+y^{2}+z^{2}=4z that lies within the paraboloid x^{2}+y^{2}=2z
The part of the surface z=xy in the first octant that lies within the cylinder x^{2}+y^{2}=a^{2}, a\gt 0
S = \dfrac{\pi}6 [(a^2+1)^{3/2} -1]
The part of the surface z=x^{2}-y^{2} in the first octant that lies within the cylinder x^{2}+y^{2}=4
The part of the sphere x^2+y^{2}+z^{2}=4z that lies between the planes z=1 and z=3.
S = 8 \pi
The part of the sphere x^{2}+y^{2}+z^{2}=4a^{2} that lies inside the cylinder x^{2}+y^{2}=2ax, a\gt 0
Applications and Extensions
Surface Area Find the surface area cut from the hyperbolic paraboloid y^{2}-x^{2}=6z by the cylinder x^{2}+y^{2}=36.
S = 6\pi\big(5\sqrt{5}-1\big)
Surface Area Find the surface area of the part of z=4-y^{2} that lies in the first octant and is enclosed by z=0, x=0, x=y, and y=2.
Surface Area Find the surface area of the part of x^{2}=y that lies in the first octant under the plane x+z=3. (Hint: Project the surface onto the xz-plane.)
S = \dfrac{1}{12} \left( 1+17\sqrt{37} +9\;\ln\;\big(6+\sqrt{37}\,\big)\right)
Surface Area Find the surface area of the part of the paraboloid z=9-x^{2}-y^{2} that lies between the planes z=0 and z=8.
Surface Area Find the surface area of the part of the hemisphere x^{2}+y^{2}+z^{2}=16, z\geq 0, that lies inside the cylinder bounded by x^{2}+y^{2}=4. See the figure.
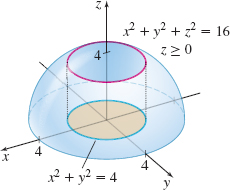
S = 16\pi \big(2 - \sqrt{3}\big)
Surface Area of the Pantheon The Pantheon in Rome is the largest unreinforced concrete dome in the world. Its inner surface is a hemisphere of diameter 43.3 \text m with an open circular ocular 9.1 \text m in diameter cut from its apex. Find the inner surface area of the dome.

 Surface Area
Surface Area- (a) Graph the surface z=10e^{-( x^{2}+y^{2})} that lies inside the cylinder x^{2}+y^{2}=4.
- (b) Find the surface area of the surface graphed in (a).
- (a)
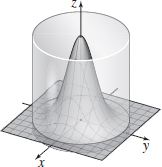
- (b) S \approx 55.436
Surface Area
- (a) Set up, but do not evaluate, the integral to find the surface area of the part of the surface z=1-x^{4}-y^{2} that lies above the 2xy-plane.
- (b)
 Graph the surface.
Graph the surface.
Derive the formula S=\pi a\sqrt{a^{2}+h^{2}} for the lateral surface area of a right circular cone of base radius a and altitude h.
See the Student Solutions Manual.
Show that the area of the first-octant portion of the plane \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1 (where a, b, and c are positive) is S=\dfrac{1}{2}\sqrt{a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}.
Use a double integral to derive the formula for the surface area of a sphere of radius R.
See the Student Solutions Manual.
Challenge Problems
Let F denote a function of three variables that possesses continuous first-order partial derivatives at each point of its domain. Suppose also that F_{z}(x,y,z) is never 0. If S is the area of the part of the surface F(x,y,z)=0 that lies over the closed, bounded region R, show that \begin{array}{rcl} S=\int\limits\int_{\kern-11ptR}\dfrac{\sqrt{[F_{x}(x,y,z)]^{2}+[F_{y}(x,y,z)]^{2}+[F_{z}(x,y,z)]^{2}}}{|F_{z}(x,y,z)|}\,d\!A \end{array}
941
Surface Area The center of a sphere of radius R is on the surface of a right circular cylinder of base radius \dfrac{R}{2}. Find the surface area of the sphere inside the cylinder. See the figure.
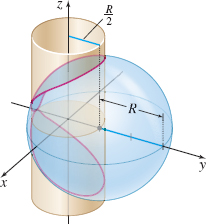
S = 2 R^2 (\pi - 2) square units
For the plane surface F(x,y,z)=Ax+By+Cz-D=0, C\neq 0, if z=f(x,y), show that the surface area S=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{ [f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}\,d\!A can be written as S=\displaystyle\iint\limits_{\kern-3ptR}\sec \gamma \,d\!A
where \gamma is the positive acute angle between the normal \mathbf{n}=A \mathbf{i}+B\mathbf{j}+C\mathbf{k} to the plane and \mathbf{k}.
