14.6 Assess Your UnderstandingPrinted Page 947
Concepts and Vocabulary
True or False A solid E in space is called xy-simple if it is enclosed on the top by a surface z=z2(x,y) and on the bottom by a surface z=z1(x,y), where z1≤z2 and z1 and z2 are continuous, and the sides of E are a cylinder whose intersection with the xy-plane forms a closed, bounded region R.
True
True or False The region R resulting from the projection onto the xy-plane of an xy-simple solid E is both x-simple and y-simple.
False
948
True or False The mass M of a solid with a mass density ρ=ρ(x,y,z) that is continuous in a region E of volume V is given by M=∭Eρ(x,y,z)dV.
True
True or False The triple integral ∭EdV can be interpreted geometrically as the area of the region R that is the projection of E onto the xy-plane.
False
Skill Building
In Problems 5–10, find each triple integral.
∭Exy2dV, E is the closed box 0≤x≤1, 0≤y≤1, 0≤z≤4.
23
∭Ex2yzdV, E is the closed box 0≤x≤2, 0≤y≤1, 0≤z≤2.
∭E(x2+y2+z2)dV, E is the closed box 0≤x≤1, 0≤y≤1, 0≤z≤1.
1
∭E(x2−y2+z2)dV, E is the closed box 0≤x≤1, 0≤y≤2, 0≤z≤1.
∭EezsinxcosydV, E is the closed box 0≤x≤π2, 0≤y≤π2, 0≤z≤1.
e−1
∭Ee−zcosxcosydV, E is the closed box 0≤x≤π2, 0≤y≤π2, 0≤z≤1.
In Problems 11–18, find each iterated triple integral.
∫20∫2−3x0∫x+y0xdzdydx
−23
∫10∫−x0∫2x+y0zdzdydx
∫30∫z+2z∫y+zy(2x+1)dxdydz
81
∫20∫y+2y∫x+yy(4z−1)dzdxdy
∫20∫10∫y0exdxdydz
2(e−2)
∫21∫z0∫√y0xex2dxdydz
∫π/20∫π/2y∫xy0sinzydzdxdy
1−π28+π348
∫π/20∫π/2x∫xy0coszxdzdydx
In Problems 19–24, find ∭ExydV.
E is the solid enclosed by the surfaces z=0 and z=5−x−y , whose projection onto the xy-plane is the region enclosed by the rectangle 0≤x≤1 and 0≤y≤3.
214
E is the solid enclosed by the surfaces z=0 and z=16−x2−y2, whose projection onto the xy-plane is the region enclosed by the rectangle 0≤x≤2 and 0≤y≤1.
E is the solid enclosed by the surfaces z=0 and z=xy, whose projection onto the xy-plane is the region enclosed by the triangle with vertices (0,0,0), (0,1,0), and (1,0,0).
1180
E is the solid enclosed by the surfaces z=0 and z=x2+y2, whose projection onto the xy-plane is the region enclosed by the triangle with vertices (0,0,0), (1,0,0), and (0,2,0).
E is the solid enclosed by the surfaces z=0 and z=3−x−y , whose projection onto the xy-plane is the region enclosed by the triangle with vertices (0,0,0), (1,1,0), and (1,−1,0).
−215
E is the solid enclosed by the surfaces z=0 and z=3+2y, whose projection onto the xy-plane is the region enclosed by the triangle with vertices (−1,0,0),(0,1,0), and (2,0,0).
In Problems 25 and 26, use a CAS to approximate each integral.
 ∫10∫x21∫√x0yexdzdydx
∫10∫x21∫√x0yexdzdydx
−0.4142
 ∫43∫32∫10ln(x2+y2+z2)dxdydz
∫43∫32∫10ln(x2+y2+z2)dxdydz
Applications and Extensions
In Problems 27–30, find each triple integral.
∭ExdV, if E is the solid enclosed by the tetrahedron having vertices at (0,0,0), (1,1,0), (1,0,0), (1,0,1).
18
∭E(x2+z2)dV, if E is the solid enclosed by the tetrahedron having vertices at (0,0,0), (1,1,0), (1,0,0), (1,0,1).
∭E(xy+3y)dV, if E is the solid enclosed by the cylinder x2+y2=9 and the planes x+z=3, y=0, and z=0.
6485
∭ExyzdV, if E is the solid enclosed by the cylinders x2+y2=1 and x2+z2=1. See the figure.

In Problems 31–34, (a) describe the solid whose volume is given by each integral.
![]() (b) Graph the solid.
(b) Graph the solid.
∫2−2∫√4−y20∫10dzdxdy
- (a) The semi-cylinder is given by x2+y2=4 and the planes x=0, z=0, and z=1.
- (b)
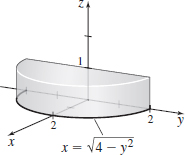
∫20∫√4−y20∫4−x2−y20dzdxdy
∫10∫x20∫y0dzdydx
- (a) The solid is bounded by y=x2 and the planes z=0, x=1, and z=y.
- (b)
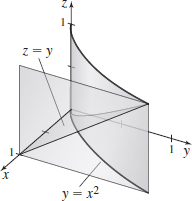
∫10∫1y2∫1−x0dzdxdy
Volume of a Solid Find the volume V of the solid enclosed by y2=z, x=0, and x=y−z.
V=160 cubic units
949
Volume of a Solid Find the volume V of the solid enclosed by z=4−y2, z=9−x, x=0, and z=0.
Set up, but do not find, ∭ExydV, where E is the solid enclosed by the surfaces z=1−x−y and z=3−x−y, whose projection onto the xy-plane is the region enclosed by the circle x2+y2=1.
V=∫1−1∫√1−x2−√1−x2∫3−x−y1−x−yxydzdydx cubic
Set up, but do not find, ∭Exy dV, where E is the solid enclosed by the surfaces z=0 and z=x2+y, whose projection onto the xy-plane is the region enclosed by the circle x2+y2=4.
In Problems 39–41, set up, but do not find, the triple integral that equals the volume of the solid,
Enclosed by z=x2+y2 and z=16−x2−y2.
V=4∫2√20∫√8−x20∫16−x2−y2x2+y2dzdydx cubic units
Enclosed by z=x2+y2 and z=2−x.
Enclosed by z2=4x and x2+y2=2x.
V=4∫20∫√1−(x−1)20∫√4x0dzdydx cubic units
 Volume
Volume- (a) Find the volume V of the solid enclosed by x2+2y2=1 and the planes z=x+1 and z=4.
- (b) Graph the solid.
Mass Find the mass M of an object in the shape of a cube of edge a if its mass density is proportional to the square of the distance from one corner.
M=ka5, where k is the constant of proportionality
Mass Set up, but do not find, the integral that equals the mass M of an object in the shape of a right circular cylinder of height h and radius a, if its mass density is proportional to the square of the distance from the axis of the cylinder.
Mass Set up, but do not find, the integral that equals the mass M of an object in the shape of a tetrahedron cut from the first octant by the plane x+y+z=1, as shown in the figure, if its mass density is proportional to the product of the distances from the three coordinate planes.
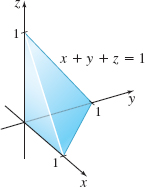
M=∫10∫1−x0∫1−x−y0k(xyz)dzdydx, where k is the constant of proportionality
 Mass A cylindrical bar of radius R and length 2L is positioned with its axis along the x-axis and its center of mass at the origin. The mass density of the bar is given by ρ(x,y,z)=kz2. Show that the mass M of the bar is M=12πkR4L.
Mass A cylindrical bar of radius R and length 2L is positioned with its axis along the x-axis and its center of mass at the origin. The mass density of the bar is given by ρ(x,y,z)=kz2. Show that the mass M of the bar is M=12πkR4L.
Moments of Inertia Set up the integrals that equal the moments of inertia Ix and Iy for the solid region enclosed by the hemisphere z=√9−x2−y2 and the xy-plane, if the mass density is proportional to the distance from the xy-plane.
Ix=∫3−3∫√9−x2−√9−x2∫√9−x2−y20k(y2+z2)zdzdydxIy=∫3−3∫√9−x2−√9−x2∫√9−x2−y20k(x2+z2)zdzdydx, where k is the constant of proportionality
Set up, but do not find, the integral of the function f(x,y,z)=x2yz over the solid enclosed by the cone 3x2+3y2=z2, z≥0, and the plane z=3.
In Problems 49 and 50, for each solid E, express the triple integral ∭Ef(x,y,z)dV as an iterated integral in six different ways.
E is the solid enclosed by the coordinate planes and the plane x+2y+3z=6.
∭Rf(x,y,z)dV=∫20∫3−3z/20∫6−2y−3z0f(x,y,z)dxdydz= ∫30∫2−2y/30∫6−2y−3z0f(x,y,z)dxdzdy=∫20∫6−3z0∫3−x/2−3z/20f(x,y,z)dydxdz= ∫60∫2−x/30∫3−x/2−3z/20f(x,y,z)dydzdx=∫30∫6−2y0∫2−x/3−2y/30f(x,y,z)dzdxdy= ∫60∫3−x/20∫2−x/3−2y/30f(x,y,z)dzdydx
E is the solid enclosed by the coordinate planes and the plane x+y+z=3.
Volume of an Ellipsoid Show that the volume of the ellipsoid x2a2+y2b2+z2c2=1 is 43πabc. (Assume that a, b, and c are positive.) What does this formula reduce to if a=b=c?
See the Student Solutions Manual. When a=b=c, the formula for the volume of an ellipsoid reduces to the formula for the volume of a sphere.
Challenge Problems
Volume of a Solid Find the volume of the solid in the first octant enclosed by the coordinate planes, a2y=b(a2−x2) and a2z=c(a2−x2), a>0, b>0, c>0.
Volume of a Solid Find the volume V of the region enclosed by z=0, z=1−x2, and z=1−y2
V=2 cubic units
Average Value of a Function The average value of f over a region R that is not necessarily rectangular is defined to be the number 1A∬Rf(x,y)dA.
- (a) In single variable calculus the average value of a function f over the closed interval [a,b] is defined to be the number 1b−a∫baf(x)dx. In what sense is this a special case of the above definition of the average value of f over R?
- (b) Let w= f(x,y,z) be integrable over a solid E in space. What definition would you give for the average value of f over E?
Show that the following integrals represent the same volume. Do not find the integrals.
- (a) 4∫40∫√16−x20∫4(x2+y2)/4dzdydx
- (b) 4∫40∫2√z0∫√4z−x20dydxdz
- (c) 4∫40∫4y2/4∫√4z−y20dxdzdy
See the Student Solutions Manual.
Show that: ∫ba∫za∫yaf(x)dxdydz=∫ba(b−x)22f(x)dx
