14.7 Assess Your UnderstandingPrinted Page 954
Concepts and Vocabulary
To convert a point P=(x,y,z) from rectangular coordinates to cylindrical coordinates (r,θ,z), use the equations: x =_____, y =_____, and z =_____.
x=rcosθ, y=rsinθ, and z=z
Expressed in cylindrical coordinates, the circular cone x2+y2=4z2 has the form _____.
r=2z
In cylindrical coordinates (r,θ,z), the differential dV of volume is _____
dV=rdrdθdz
True or False In cylindrical coordinates, ∭Erdrdθdz equals the volume of the solid E.
True
Skill Building
In Problems 5–12, find the cylindrical coordinates (r,θ,z) of each point with the given rectangular coordinates.
(−√3,−1,−5)
(2,7π6,−5)
(−1,√3,4)
(1,1,√2)
(√2,π4,√2)
(2,−2,4)
(2,0,4)
(2,0,4)
(−1,0,12)
(0,3,4)
(3,π2,4)
(0,1,−3)
In Problems 13–18, find the rectangular coordinates (x,y,z) of each point with the given cylindrical coordinates.
(2,π6,−5)
(√3,1,−5)
(4,π3,3)
(1,0,8)
(1,0,8)
(4,π6,2)
(2,π2,0)
(0,2,0)
(−3,π2,1)
In Problems 19–22, give a geometric interpretation of each triple integral.
∫1−1∫√1−x2−√1−x2∫√1−x2−z20dydzdx
The triple integral represents the volume of a hemisphere of radius 1 to the right of the xz-plane, that is y≥0.
955
∫10∫√1−z20∫√1−y2−z20dxdydz
∫20∫√4−x2−√4−x2∫√x2+y20dzdydx
The triple integral represents the volume inside the vertical cylinder x2+y2=4, bounded below by the xy-plane and bounded above by the surface of the cone z=√x2+y2.
∫30∫√9−x2−√9−x2∫√x2+z20dydzdx
In Problems 23–26, find each iterated integral.
∫π/2π/6∫30∫rsinθ0rcsc3θdzdrdθ
9√3
∫π/2π/6∫10∫sinθ0rcosθsinθdzdrdθ
∫π/30∫10∫e−10rdzdrdθ
π6e
∫π/30∫sinθ0∫rsinθ0rdzdrdθ
In Problems 27–32, find each triple integral by converting to cylindrical coordinates.
∭EdV, where E is the solid enclosed by the planes z=1 and z=4, and the cylinders x2+y2=1 and x2+y2=9.
24π
∭EdV, where E is the solid enclosed by the xy-plane, z=3, and the cylinder x2+y2=4.
∭EydV, where E is the solid enclosed by the planes z=1 and z=x+3, and the cylinders x2+y2=1 and x2+y2=4.
0
∭ExdV, where E is the solid enclosed by the planes z=0 and z=x, and the cylinder x2+y2=9.
∭ExydV, where E is the solid enclosed by the surfaces z=1−x−y and z=3−x−y, whose projection onto the xy-plane is the circle x2+y2=1.
0
∭ExydV, where E is the solid enclosed by the surfaces z=0 and z=x2+y2, whose projection onto the xy-plane is the circle x2+y2=4.
Applications and Extensions
Volume Find the volume of the solid enclosed by the intersection of the sphere x2+y2+z2=9 and the cylinder x2+y2=2.
V=4π(9−7√73) cubic units
Volume Find the volume of the solid enclosed by the intersection of the sphere x2+y2+z2=4 and the cylinder x2+y2=2x.
Volume Find the volume V of the solid enclosed by z=x2+y2 and z=16−x2−y2.
V=64π cubic units
Volume Find the volume V of the solid enclosed by z=x2+y2 and z=2−x.
Volume Find the volume V of the solid enclosed by z2=4x and x2+y2=2x.
V=128√215 cubic units
Mass Find the mass of a homogeneous solid of mass density ρ in the shape of a sphere of radius a.
Mass Find the mass of a solid in the shape of a sphere of radius a, if the mass density ρ is proportional to the square of the distance from the center.
M=4kπa55, where k is the constant of proportionality
Mass Find the mass M of an object in the shape of a right circular cylinder of height h and radius a, if its mass density is proportional to the square of the distance from the axis of the cylinder.
Moments of Inertia Find the moments of inertia Ix and Iy for the solid region enclosed by the hemisphere z=√9−x2−y2 and the xy-plane, if the mass density is proportional to the distance from the xy-plane.
Ix=Iy=2438kπ, where k is the constant of proportionality
Center of Mass Find the center of mass of a homogeneous solid in the first octant enclosed by the surface z=xy and the cylinder x2+y2=4.
Center of Mass Find the center of mass of a homogeneous solid enclosed by the surface x2+y2=4z and the plane z=2.
(ˉx,ˉy,ˉz)=(0,0,43)
Center of Mass Find the center of mass of a homogeneous solid enclosed by the inside of the sphere x2+y2+z2=12 and above the paraboloid z=x2+y2.
Center of Mass Find the center of mass of a homogeneous solid enclosed by the paraboloid z=x2+y2 and the plane z=4.
(ˉx,ˉy,ˉz)=(0,0,83)
Mass Use cylindrical coordinates to find the mass of the homogeneous solid bounded on the sides by x2+y2=1, on the bottom by the xy-plane, and on the top by x2+y2+z2=2.
Joint Between Two Rods Find the mass of the intersection of two rods with constant mass density ρ that is formed by the cylinders x2+y2=1 and x2+z2=1.
M=163ρ
 Volume of a Mountain The height of a mountain (in km) can be approximated by z=5.3e−(x2+y2).
Volume of a Mountain The height of a mountain (in km) can be approximated by z=5.3e−(x2+y2).- (a) Sketch the mountain over the region x2+y2≤4.
- (b) Find the volume of the mountain over the region x2+y2≤4.
In Problems 49 and 50, each integral is given in cylindrical coordinates. Express each integral in rectangular coordinates. Do not integrate.
∫2π0∫40∫√16−r2−rz2r5cos4θdzdrdθ
∫4−4∫√16−x2−√16−x2∫√16−x2−y2−√x2+y2x4z2dzdydx
∫π/20∫20∫9−r2z2r4sin4θdzdrdθ
956
Challenge Problems
Volume A circular hole of radius r is drilled through a sphere of radius R>r, as shown in the figure.
- (a) Find r in terms of R so that the hole removes exactly half of the volume of the sphere. (Hint: set up a volume integral in cylindrical coordinates for the hole.)
- (b) Find r rounded to three decimal places if R=10cm.
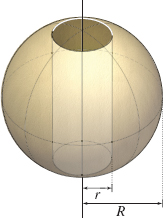
- (a) r=R√22/3−122/3 cm
- (b) r≈6.083 cm
Volume Find the volume enclosed on the top by the sphere x2+y2+z2=5 and on the bottom by the paraboloid x2+y2=4z.
Volume of a Joint Two pipes intersect at right angles as shown in the figure. Find the inner radius r of the pipes to ensure the volume of the intersecting joint is 10m3.
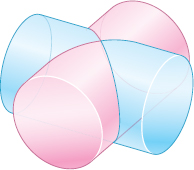
r=3√152 m
