Question

True or False \(\int_{0}^{2}\big[\int_{0}^{1}xy^{2}{\it dy}\big] {\it dx}=\big[\int_{0}^{2}x\,{\it dx}\big]\cdot \big[\int_{0}^{1}y^{2}{\it dy}\big]\).

Question

True or False Fubini’s Theorem states that if a function \(z=f(x,y) \) is continuous on a closed rectangular region \(R\) defined by \(a\leq x\leq b\) and \(c\leq y\leq d\), then \(\int_{c}^{d} \big[ \int_{a}^{b}f(x,y)\,{\it dx}\big] {\it dy}=\int_{a}^{b}\big[ \int_{c}^{d}f(x,y)\,{\it dx}\big] {\it dy}.\)

Question

Multiple Choice The result of integrating \( \int_{1}^{4}x^{2}\sqrt{y}\,{\it dy}\) is [(a) a number, (b) a function of \(y,\) (c) a function of \(x\) and \(y\), (d) a function of \(x\)].

Question

True or False If a function \(z=f(x,y) \) is continuous on a closed, rectangular region \(R,\) then the double integral \( \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\) exists.

Question

Let \(f(x,y) =x(3-y) \) be defined over the region \(R\) shown in the figure.

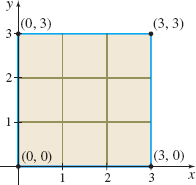
1. Find the Riemann sum of \(f\) over \(R\) by partitioning the region into nine congruent subsquares with sides \(\Delta x_{i}=1,\) \(i=1,2,3,\) and \(\Delta y_{j}=1,\) \(j=1,2,3\).
   
   Choose the lower right corner of each subsquare as \((u_{k},v_{k})\), \(k=1,2,3,\ldots , 9.\)
2. Find the Riemann sum of \(f\) over the partition used in (a) but choose the upper left corner of each subsquare as \((u_{k},v_{k})\), \(k=1,2,3,\ldots , 9.\)

Question

Let \(f(x,y) =3xy^{2}\) be defined over the rectangular region \(R\) defined by \(0\leq x\leq 6,\) \(0\leq y\leq 4.\)

1. Find the Riemann sum of \(f\) over \(R\) by partitioning the region into six congruent subsquares, with sides \(\Delta x_{i}=2,\) \(i=1,2,3,\) and \( \Delta y_{j}=2,\) \(j=1,2\). Choose the lower left corner of each subsquare as \( (u_{k},v_{k})\), \(k=1,2,3,\ldots , 6.\)
2. Find the Riemann sum of \(f\) over the partition used in (a) but choose the lower right corner of each subsquare as \((u_{k},v_{k})\), \(k=1,2,3, \ldots , 6.\)

Question

Let \(f(x,y) =x^{2}+y\) be defined over the rectangular region \(R\) defined by \(1\leq x\leq 5,\) \(2\leq y\leq 4.\)

1. Find the Riemann sum of \(f\) over \(R\) by partitioning the region into four congruent subrectangles with sides \(\Delta x_{i}=2,\) \(i=1,2,\) and \(\Delta y_{j}=1,\) \(j=1,2\). Choose the lower left corner of each subrectangle as \( (u_{k},v_{k})\), \(k=1,2,3,4.\)
2. Find the Riemann sum of \(f\) over the partition used in (a) but choose the upper right corner of each subrectangle as \((u_{k},v_{k})\), \(k=1,2,3,4.\)

Question

Let \(f(x,y) =x\left( 1-y\right) \) be defined over the rectangular region \(R\) defined by \(0\leq x\leq 3,\) \(0\leq y\leq 4.\)

1. Find the Riemann sum of \(f\) over \(R\) by partitioning the region into six congruent subrectangles with sides \(\Delta x_{i}=1,\) \(i=1,2,3,\) and \(\Delta y_{j}=2,\) \(j=1,2.\) Choose the lower left corner of each subrectangle as \( (u_{k},v_{k})\), \(k=1,2,3,\ldots ,6.\)
2. Find the Riemann sum of \(f\) over the partition used in (a) but choose the upper left corner of each subrectangle as \((u_{k},v_{k})\), \(k=1,2,3,\ldots ,6.\)

Question

Find the Riemann sum for Example 1 if \(R\) is divided into four congruent subsquares. Choose \((u_{k},v_{k}),\) \(k=1,2,3,4,\) as the center of the \(k\)th subsquare.

Question

Find the Riemann sum for Example 1 if \(R\) is divided into eight congruent subrectangles with \(\Delta x_{i}=1,\) \(i=1,2,3,4\), and \(\Delta y_{j}=2,\) \(j=1,2\). Choose \((u_{k},v_{k}),\) \(k=1,2,3,\ldots ,8,\) as the center of the \(k\)th subrectangle.

Question

\(\int_{1}^{e}\dfrac{x}{y}dy\)

Question

\(\int_{0}^{2}\dfrac{x}{y}{\it dx}\)

Question

\(\int_{0}^{\pi /2}x\sin y\,{\it dx}\)

Question

\(\int_{0}^{\pi /2}x\sin y\,{\it dy}\)

Question

\(\int_{0}^{1}e^{x}\,{\it dx}\)

Question

\(\int_{0}^{1}e^{x}\,{\it dy}\)

Question

\(\displaystyle\int_{0}^{1}\left[ \int_{0}^{2}x^{2}y\,{\it dy}\right] \! {\it dx}\)

Question

\(\displaystyle\int_{0}^{2}\left[ \int_{0}^{4}x^{2}y\,{\it dx} \right] \! {\it dy}\)

Question

\(\displaystyle\int_{0}^{3}\left[ \int_{0}^{2}3xy\,{\it dy}\right] \! {\it dx}\)

Question

\(\displaystyle\int_{0}^{2}\left[ \int_{0}^{1}3xy\,{\it dx}\right] \! {\it dy}\)

Question

\(\displaystyle\int_{-1}^{1}\left[ \int_{0}^{1}3x^{2}y^{2}\,{\it dx} \right] \! {\it dy}\)

Question

\(\displaystyle\int_{0}^{1}\left[\int_{0}^{2}3x^{2}y^{2}\,{\it dy}\right] \! {\it dx}\)

Question

\(\displaystyle\int_{0}^{2}\left[ \int_{-1}^{1}2xy^{2}\,{\it dx}\right] \! {\it dy}\)

Question

\(\displaystyle\int_{-1}^{1}\left[ \int_{1}^{2}2xy^{2}\,{\it dy} \right] \! {\it dx}\)

Question

\(\displaystyle\int_{0}^{\pi /4}\left[\int_{0}^{2}x\cos y\,{\it dx}\right] \! {\it dy}\)

Question

\(\displaystyle\int_{0}^{2}\left[ \int_{0}^{\pi /3}x\cos y\,{\it dy}\right] \! {\it dx}\)

Question

\(\displaystyle\int_{0}^{3}\left[ \int_{0}^{\pi /3} (4x-3) ^{2}\sin y\,{\it dy}\right]\! {\it dx}\)

Question

\(\displaystyle\int_{0}^{\pi /3}\left[ \int_{0}^{3}(4x-3) \sin y\,{\it dx}\right] \! {\it dy}\)

Question

\(\displaystyle\int_{0}^{1}\left[ \int_{0}^{\pi /2}e^{x}\cos y\,{\it dy} \right]\! {\it dx}\)

Question

\(\displaystyle\int_{0}^{\pi /4}\left[ \int_{0}^{1}e^{x}\cos y\,{\it dx}\right]\! {\it dy}\)

Question

\(\displaystyle\int_{0}^{2}\left[ \int_{-\pi /2}^{\pi /2}\dfrac{\sin y}{2x+1}\,{\it dy}\right]\! {\it dx}\)

Question

\(\displaystyle\int_{0}^{\pi /2}\left[ \int_{0}^{2}\dfrac{\sin y}{2x+1} \,{\it dx}\right]\! {\it dy}\)

Question

\(\displaystyle\int_{0}^{\pi/2}\left[ \int_{0}^{2}xe^{x}\sin y\,{\it dx}\right]\! {\it dy}\)

Question

\(\displaystyle\int_{0}^{1}\left[ \int_{0}^{\pi/2}xe^{x}\sin y\,{\it dy}\right]\! {\it dx}\)

Question

\(\displaystyle\int_{1}^{2}\left[ \int_{0}^{\pi /2}\dfrac{x\cos x}{y}\,{\it dx} \right]\! {\it dy}\)

Question

\(\displaystyle\int_{0}^{\pi /3}\left[ \int_{1}^{2}\dfrac{x\cos x}{y}\,{\it dy}\right]\! {\it dx}\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR} ( 2x+y^{2})\, {\it dA}, \quad 0\leq x\leq 2,\) \( 0\leq y\leq 3\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}( x^{2}-3y)\, {\it dA}, \quad -1\leq x\leq 2,\) \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x( x^{2}+5) \, {\it dA}, \quad 0\leq x\leq 2,\) \( -1\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}\sqrt{y}( 3x^{2}+x)\, {\it dA}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 4\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}2xe^{y}{\it dA}, \quad -3\leq x\leq 2,\) \( 0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}e^{2x+y}{\it dA}, \quad 0\leq x\leq 1,\) \(-1\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x\sec ^{2}y\,{\it dA}, \quad 0\leq x\leq 3,\) \(0\leq y\leq \dfrac{\pi }{4}\)

Question

\(\displaystyle\iint\limits_{R}y^{2}\sec x\tan x\,{\it dA}, \quad 0\leq x\leq \dfrac{\pi }{3},\) \(-1\leq y\leq 3\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}\dfrac{x}{2y+3}\,{\it dA}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}\dfrac{y^{2}}{x-3}\,{\it dA}, \quad 4\leq x\leq 5,\) \(0\leq y\leq 3\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x\sin (xy)\, {\it dA}, \quad 0\leq x\leq \dfrac{\pi }{2}\), \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}y\cos (xy)\, {\it dA}, \quad 0\leq x\leq 1\), \(\dfrac{\pi }{2}\leq y\leq 2\pi \)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x^{3}\cos ( x^{2}y)\, {\it dA}, \quad 0\leq x\leq \dfrac{\pi }{2}\), \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x^{3}\sin ( x^{2}y)\, {\it dA}, \quad 0\leq x\leq \dfrac{\pi }{2}\), \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}\dfrac{y^{2}}{(1+xy^{2}) ^{3}}\,{\it dA}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 3\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}( x^{3}+x) ( x^{2}y+y)\, {\it dA}, \quad 0\leq x\leq 1,\) \(0\leq y\leq 1\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}y^{5}e^{xy^{3}}{\it dA}, \quad 0\leq x\leq 1,\) \(0\leq y\leq 2\)

Question

\(\displaystyle\iint\limits_{\kern-3ptR}x^{5}ye^{x^{3}y^{2}}{\it dA}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 1\)

Question

\(f(x,y)=x+2y, \quad 0\leq x\leq 1,\) \(0\leq y\leq 2\)

Question

\(f(x,y)=2x+3y, \quad 0\leq x\leq 2,\) \(0\leq y\leq 3\)

Question

\(f(x,y)=x^{2}+y^{2}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 1\)

Question

\(f(x,y)=4x^{2}+3y^{2}, \quad 0\leq x\leq 3,\) \(-2\leq y\leq 1\)

Question

\(f(x,y)=\sin x, \quad 0\leq x\leq \dfrac{\pi }{2},\) \(0\leq y\leq 1\)

Question

\(f(x,y)=\cos y, \quad 0\leq x\leq 1,\) \(0\leq y\leq \dfrac{\pi }{2}\)

Question

\(f(x,y)=\dfrac{x^{2}+y^{2}}{xy} \quad 1\leq x\leq 2,\) \(1\leq y\leq 2\)

Question

\(f(x,y)=\dfrac{y^{2}}{x^{2}}, \quad 1\leq x\leq 2,\) \(1\leq y\leq 2\)

Question

\(f(x,y)=e^{x+y}, \quad 0\leq x\leq 2,\) \(0\leq y\leq 1\)

Question

\(f(x,y)=e^{x-y}, \quad 0\leq x\leq 2,\) \(1\leq y\leq 2\)

Question

Volume Find the volume of the solid below the paraboloid \( z=x^{2}+y^{2}\) and above the square in the \(xy\)-plane enclosed by the lines \( x=\pm 1\) and \(y=\pm 1\).

Question

Show that \(\displaystyle\iint\limits_{\kern-3ptR}{\it dA}=\int_{c}^{d}\big[ \int_{a}^{b}{\it dx}\big] {\it dy} =(b-a) (d-c) \). That is, show that the volume of a solid with height \(1\), \(\displaystyle\iint\limits_{\kern-3ptR}{\it dA},\) defined over a rectangular region \(a\leq x\leq b,\) \(c\leq y\leq d\) is numerically equal to the area of the rectangle.

Question

Average Value of a Function Suppose that \(z=f(x,y)\) is integrable over a closed, rectangular region \(R\) in the \(xy\)-plane. Let \(P\) be a partition of \(R\) into \(N\) subrectangles of equal area \(\Delta A\). Evaluate \(f\) at the center \((u_{k},v_{k})\) of the \(k\)th subrectangle \( (k=1,2,\ldots ,N)\), and let AVG be the average of these \(N\) values.

1. Show that \({\it AVG}=\dfrac{1}{A}\sum\limits_{k=1}^{N}f(u_{k},v_{k}) \Delta A\), where \(A\) is the area of \(R\).
2. Explain why \[ \lim_{\Vert P\Vert \rightarrow 0}{\it AVG}=\dfrac{1}{A}\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA} \]
   (This is called the average value of \(f\) over \(R\).)

Question

\(f(x,y) =y\cos x, \quad 0\leq x\leq \pi ,\) \(1\leq y\leq 5\)

Question

\(f(x,y) =\dfrac{xy}{x^{2}+1}, \quad 0\leq x\leq 1,\) \(0\leq y\leq 2\)