14.4 Assess Your UnderstandingPrinted Page 934
Concepts and Vocabulary
If a lamina represented by a closed, bounded region R has a continuous mass density function ρ=ρ(x,y), then the double integral ∬ gives the _____ of the lamina.
Mass
True or False If a lamina represented by a closed, bounded region R has a continuous mass density function \rho =\rho (x, y) , then \iint\limits_{\kern-3ptR}y\,\rho (x, y)\,{\it dA} is called the moment of mass about the y-axis.
False
If a lamina represented by a closed, bounded region R has a continuous mass density function \rho =\rho (x, y) , the moment of mass about the y-axis M_{y} is given by the double integral _____.
M_y = \iint\limits_{\hspace{-3pt}R\hspace{3pt}} x \rho(x,y) \, dA
True or False Center of mass and centroid are synonyms.
False
True or False The moment of mass M_a of a particle about the a-axis measures the tendency of the particle to rotate about the a-axis.
True
True or False The moment of inertia about the origin equals the difference between the moment of inertia about the x-axis and the moment of inertia about the y-axis.
False
Skill Building
Find the mass M and center of mass (\bar{x}, \bar{y}) of the triangular lamina shown in the figure. The mass density function of the lamina is \rho =\rho (x, y) =x^{2}y.
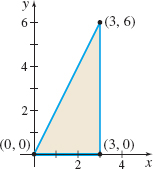
M = \dfrac{486}5 and (\bar{x}, \bar{y}) = \left( \dfrac52, \dfrac{10}3 \right)
Find the mass M and the center of mass (\bar{x}, \bar{y}) of the square lamina shown in the figure. The mass density function of the lamina is \rho =\rho (x, y) =xy^{2}.
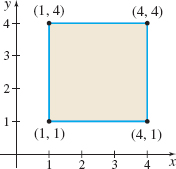
In Problems 9–20, find the mass and center of mass of each lamina.
The lamina enclosed by the lines x=2 and y=4, and the coordinate axes, and whose mass density is \rho =\rho (x, y) =3x^{2}y
M = 64 and (\bar{x}, \bar{y}) = \left( \dfrac32, \dfrac83\right)
The lamina enclosed by the lines x=1 and y=2, and the coordinate axes, and whose mass density is \rho =\rho (x, y) =2x^{2}y^{2}
The lamina in the first quadrant enclosed by y^{2}=x, x=1, and the x-axis, and whose mass density is \rho =\rho (x, y) =2x+3y
M = \dfrac{31}{20} and (\bar{x}, \bar{y}) = \left( \dfrac{150}{217}, \dfrac{44}{93} \right)
The lamina in the first quadrant enclosed by y^{2}=4x, \ x=1, and the x-axis, and whose mass density is \rho =\rho (x, y) =x+1
The lamina enclosed by y^{2}=x and y=x, and whose mass density \rho =\rho (x, y) is proportional to the distance from the y-axis
M = \dfrac{k}{15}, where k is the constant of proportionality, and (\bar{x}, \bar{y}) = \left( \dfrac{15}{28}, \dfrac58 \right)
The lamina enclosed by y=\sin x and the x-axis, 0\leq x\leq \pi , and whose mass density \rho =\rho (x, y) is proportional to the distance from the x-axis
The lamina enclosed by the lines 2x+3y=6, x=0, and y=0, and whose mass density \rho =\rho (x, y) is proportional to the sum of the distances from the coordinate axes
M = 5k, where k is the constant of proportionality, and (\bar{x}, \bar{y}) = \left(\dfrac65, \dfrac{7}{10} \right)
935
The lamina enclosed by the lines 3x+4y=12, x=0, and y=0, and whose mass density \rho =\rho (x, y) is proportional to the product of the distances from the coordinate axes
The lamina enclosed by the cardioid r=1+\sin \theta, and whose mass density \rho =\rho (r, \theta) is proportional to the distance from the pole
M = \dfrac{5k\pi}3, where k is the constant of proportionality, and (\bar{x}, \bar{y}) = \left(0, \dfrac{21}{20} \right)
The lamina enclosed by r=\cos \theta , -\dfrac{\pi}{2}\leq \theta \leq \dfrac{\pi}{2}, whose mass density \rho =\rho (r,\theta) is proportional to the distance from the pole
A lamina inside the graph of r=2a\sin \theta and outside the graph of r=a, whose mass density \rho =\rho (r, \theta) is inversely proportional to the distance from the pole
M = 2ka \left(\sqrt{3} - \dfrac{\pi}3 \right) \approx 1.370 k a, where k is the constant of proportionality, and (\bar{x}, \bar{y}) = \left(0, \dfrac{3\sqrt{3}a}{2\big(3\sqrt{3} - \pi\big)} \right) \approx (0,1.265 a)
A lamina outside the limaçon r=2-\cos \theta and inside the circle r=4\cos \theta , whose mass density \rho =\rho (r,\theta) is inversely proportional to the distance from the pole
In Problems 21–26, find the moment of inertia about the indicated axis for each homogeneous lamina of mass density \rho .
The lamina enclosed by the lines 2x+3y=6, x=0, and y=0 about the x-axis
I_x = 2 \rho
Rework Problem 21 for the moment of inertia about the y-axis.
The lamina in the first quadrant enclosed by the lines x=a and y=b about the y-axis
I_y = \dfrac{\rho a^3 b}3
Rework Problem 23 for the moment of inertia about the x-axis.
The lamina enclosed by y=x^{2} and y=2-x^{2}; about the y-axis
I_y = \dfrac{8}{15} \rho
The lamina enclosed by the loop of y^{2}=x^{2}(4-x); about the y-axis
Applications and Extensions
Mass Find the mass of a flat circular washer with inner radius a and outer radius 2a if its mass density \rho =\rho (x, y) is inversely proportional to the square of the distance from the center. See the figure.

M = 2 \pi\;k\;\ln\;2, where k is the constant of proportionality
Mass Rework Problem 27 if the mass density \rho =\rho (x, y) is inversely proportional to the distance from the center.
Mass and Center of Mass Find the mass and center of mass of a lamina in the shape of the region enclosed on the left by the line x=a, a\gt0, and on the right by the circle r=2a\cos \theta if its mass density \rho is inversely proportional to the distance from the y-axis.
M = ka(\pi - 2) \approx 1.142 ka, where k is the constant of proportionality, and (\bar{x},\bar{y}) = \left( \dfrac{a \pi}{2(\pi - 2)} , 0 \right) \approx (1.376 a, 0)
Mass and Center of Mass Find the mass and center of mass of a lamina in the shape of the smaller region cut from the circle r=6 by the line r\cos \theta =3 if its mass density is \rho =\rho (r,\theta) =\cos ^{2}\theta .
Mass Find the mass of the lamina enclosed by y=x^{2} and y=x^{3}; the mass density is \rho =\rho (x,y) =\sqrt{xy}.
M = \dfrac{1}{27}
Center of Mass Find the center of mass of the lamina inside r=4\cos \theta and outside r=2\sqrt{3} if the mass density \rho =\rho (r, \theta) is inversely proportional to the distance from the origin.
Center of Mass Find the mass and the center of mass of the lamina enclosed by x=y-2 and x=-y^{2}, if the mass density is \rho =\rho (x,y) =x^{2}.
M = \dfrac{423}{28} and (\bar{x},\bar{y}) = \left( -\dfrac{574}{235}, -\dfrac{469}{470}\right)
Center of Mass Find the center of mass of the lamina enclosed by y=x^{2} and x-2y+1=0, if the mass density is \rho =\rho (x,y) =2x+8y+2.
Center of Mass Find the center of mass of the homogeneous lamina enclosed by bx^{2}=a^{2}y and ay=bx, a \gt 0, b \gt 0.
(\bar{x},\bar{y}) = \left( \dfrac{a}{2}, \dfrac{2b}{5} \right)
 Center of Mass Find the center of mass of the homogeneous lamina enclosed by y=\ln x, the x-axis, and the line x=e^{2}.
Center of Mass Find the center of mass of the homogeneous lamina enclosed by y=\ln x, the x-axis, and the line x=e^{2}.
Moment of Inertia The mass density at each point of a circular washer of inner radius a and outer radius b is inversely proportional to the square of the distance from the center.
- (a) Find the mass of the washer. Then discuss its behavior as a\rightarrow 0^+. (Note that the mass density becomes unbounded as we approach the center of the washer.)
- (b) Find the moment of inertia of the washer about its center, and show that (unlike the mass) it remains finite as a\rightarrow 0^+.
- (a) M = 2 \pi\;k\;\ln \left( \dfrac{b}{a} \right), where k is the constant of proportionality. As a \to 0^+, M \to \infty.
- (b) I = k \pi (b^2-a^2), where k is the constant of proportionality. As a \to 0^+, I \to k \pi b^2.
 Moment of Inertia
Moment of Inertia- (a) Graph the limaçon r=3+2\cos \theta and the circle r=2.
- (b) Set up the integral for the moment of inertia about the x-axis of the lamina inside the limaçon and outside the circle from (a) if the mass density \rho of the lamina is inversely proportional to the square of the distance from the origin.
- (c) Find the integral in (b).
Show that the center of mass of a rectangular homogeneous lamina lies at the intersection of its diagonals.
See the Student Solutions Manual.
A homogeneous lamina is in the shape of the region enclosed by a right triangle of base b and height h. Show that its moment of inertia about the base is \dfrac{1}{6}mh^{2}, where m is the mass of the lamina. (Hint: Position the triangle so that the base lies on the positive x-axis from (0, 0) to (b, 0).)
Challenge Problems
Show that the center of mass of the region enclosed by a triangular homogeneous lamina lies at the point of intersection of its medians. (Hint: Position the triangle so that its vertices are at (a, 0), (b, 0), and (0, c), where a \lt 0, b \gt 0, and c \gt 0)
See the Student Solutions Manual.
Suppose that a homogeneous lamina occupies a region R in the xy-plane. Show that the average value of f(x, y)=x over R is \bar{x}, the first coordinate of the center of mass of the lamina. What is the average value of g(x, y)=y over R? [Hint: The average value of f over a region R is defined to be the number \dfrac{1 }{A}\iint\limits_{\kern-3ptR}f(x, y)\,{\it dA}.]
- (a) Show that the moment of inertia about the z-axis of the thin flat plate in the figure equals the sum of its moments of inertia about the x- and y-axes.
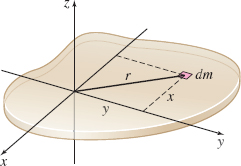
936
- (b) Given that the moment of inertia of a homogeneous disk about an axis through its center and perpendicular to its plane is \dfrac{mR^{2}}{2} (where m is mass and R is the radius), use (a) to find its moment of inertia about a diameter.
- (c) What is the moment of inertia of a disk about an axis tangent to its edge?
- (a) Show that the moment of inertia about the z-axis of the thin flat plate in the figure equals the sum of its moments of inertia about the x- and y-axes.
- (a) See the Student Solutions Manual.
- (b) I = \dfrac{mR^2}4
- (c) I = \dfrac{5mR^2}4
