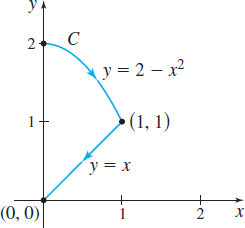15.2 Assess Your UnderstandingPrinted Page 987
987
Concepts and Vocabulary
True or False A line integral ∫Cf(x,y)ds is equal to a definite integral if C is a smooth curve defined on [a,b], and if the function f is continuous on some region that contains the curve C.
True
If C is a smooth curve defined by the parametric equations x=x(t) and y=y(t), a≤t≤b, and f is a function that is continuous on some region that contains the curve C, then the line integral of f along C from t=a to t=b exists and is given by ∫Cf(x,y)ds=∫ba__________dt.
f(x(t),y(t))√(dxdt)2+(dydt)2
True or False The value ∫Cf(x,y)ds depends on the choice of the parametric equations used to represent the smooth curve C.
False
If the variable mass density of a wire at a point (x,y) is ρ(x,y), then the mass M of the wire can be found using the line integral _______, where C is the curve representing the shape of the wire.
∫Cρ(x,y)ds
True or False ∫−C(Pdx+Qdy)=∫C(Pdx−Qdy)
False
True or False A piecewise-smooth curve C consists of a finite number of smooth curves that are joined together end to end.
True
If a piecewise-smooth curve C consists of smooth curves C1,C2,…,Cn, n≥2, then ∫C(Pdx+Qdy)=_________.
∫C1(Pdx+Qdy)+∫C2(Pdx+Qdy)+⋯+∫Cn(Pdx+Qdy)
True or False Suppose C is a smooth curve defined by the parametric equations x=x(t), y=y(t), and z=z(t), a≤t≤b, and P(x,y,z), Q(x,y,z), and R(x,y,z) are functions that are continuous on some solid in space containing C, then ∫CP(x,y,z)dx=∫baP(x(t),y(t),z(t))x(t)dt.
False
Skill Building
In Problems 9–14, find each line integral for the given smooth curve C.
∫Cx2yds;C: x=cost, y=cost , 0≤t≤π2
√24
∫C(y−x2)ds;C: x=t, y=3t, 0≤t≤1
∫Cxyds;C: x=t2, y=4t, 0≤t≤2
51215(1+√2)
∫Cxds;C: x=t, y=3t2, 0≤t≤1
∫Cy2x2−y2ds;C: x=t, y=t, 1≤t≤5
√2ln5
∫Cx2x3+y3ds;C: x=3t, y=4t, 1≤t≤2
Find ∫C2yds, where C is the curve y=12x3 joining (0,0) to (2,4).
7427√37−227
Find ∫Cxds, where C is the curve x=5y3 joining (0,0) to (5,1).
Find ∫C(xy+1)ds, where C is the curve r(t)=sinti+costj, 0≤t≤π.
π
Find ∫Cxy2ds, where C is the curve r(t)=costi+sintj, 0≤t≤π2.
In Problems 19–22, find each line integral along the two given curves C1andC2.
∫C(x+y2)ds
- (a) C1: x=t, y=t, 0≤t≤1
- (b) C2: x=sint, y=sint, 0≤t≤π2
- (a) 56√2
- (b) 56√2
∫C(x+y)ds
- (a) C1: x=t, y=3t, 0≤t≤1
- (b) C2: x=sin(2t), y=3sin(2t), 0≤t≤π2
∫C(x+ey)ds
- (a) C1: x=1−t, y=t, 0≤t≤1
- (b) C2: x=cost, y=1−cost, 0≤t≤π2
- (a) √2e−12√2
- (b) √2e−12√2
∫Cxex2ds
- (a) C1: x=t+1, y=t, 0≤t≤1
- (b) C2: x=1+sint, y=sint, 0≤t≤π2
In Problems 23–26, find the line integral with respect to x and with respect to y for each function f(x,y) along the given curve C.
f(x,y)=2x+y2 along the line y=3−x from (0,3) to (3,0).
∫Cf(x,y)dx=18;∫Cf(x,y)dy=−18
f(x,y)=xey along the line 2x−y=1 from (0,−1) to (1,1).
f(x,y)=xey along the curve C traced out by x=e2y from (1,0) to (e2,1).
∫Cf(x,y)dx=25(e5−1);∫Cf(x,y)dy=13(e3−1)
f(x,y)=x2y along the parabola x=2y2 from (0,0) to (2π,√π).
Find ∫C(x2ydx+xydy) along the curve C: x2+y2=1 from (1,0) to (0,1) using the following parametric equations:
- (a) x=cost, y=sint, 0≤t≤π2
- (b) x=√1−y2, 0≤y≤1
- (a) 13−π16
- (b) 13−π16
Find ∫C(xydx+xy2dy) along the curve C: x2+y2=9 from (3,0) to (−3,0) traced out by the parametric equations:
- (a) x=3cost, y=3sint, 0≤t≤π
- (b) y=√9−x2, −3≤x≤3
Find ∫C[y2dx+(xy−x2)dy] along each of the given curves from (0,0) to (1,3):
- (a) C is the line y=3x.
- (b) C is the parabola y2=9x.
- (a) 5
- (b) 6.15
Find ∫C[(x2+y2)dx+3x2ydy] along each of the given curves from (−2,4) to (2,4):
- (a) C is the parabola y=x2.
- (b) C is the line y=4.
988
In Problems 31–34, find ∫C[(x+2y)dx+(2x+y)dy] along each curve C.
C is the curve y=x2 from (0,0) to (1,1).
3
C is the curve y=x3 from (0,0) to (1,1).
C is the curve x=cost, y=sint, 0≤t≤π2.
0
C is the curve x=1−t, y=t, 0≤t≤1.
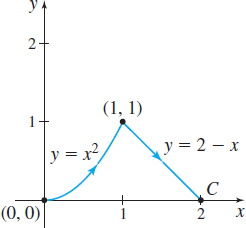
In Problems 35–38, find ∫Cxds along each piecewise-smooth curve C.
512√5−112−12√2
4√2−4
Find ∫C[(xcosy)dx−(ysinx)dy], where C consists of line segments connecting the points (0,0), (1,0), (1,1) , and (0,1), in that order.
12(1−sin1−cos1)
Find ∫C[(xsiny)dx−(ycosx)dy], where C consists of line segments connecting the points (0,0), (0,1), (1,1), and (1,0), in that order.
Find ∫C(yzdx+xzdy+xydz), where C consists of line segments connecting the points (0,0,0), (1,0,0), (1,1,0), and (1,1,1), in that order.
1
Find ∫C[yzdx+(y+zx)dy+xzdz], where C consists of line segments connecting the points (0,0,0), (1,0,0), (1,2,0), and (1,2,1), in that order.
In Problems 43–46, find ∫C[ydx+(x−16y)dy] along each of the given curves from (2,0) to (0,4).
The line segment joining the two points
−128
The parabola y=4−x2
The line segment from (2,0) to (2,2), followed by the line segment from (2,2) to (0,4).
−128
The parabola y=4−x2 from (2,0) to (1,3), followed by the line segment from (1,3) to (0,4).
In Problems 47–50, for each vector field F and curve C: r=r(t), find \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}.
\mathbf{F}(x,y)=(x+2y)\mathbf{i}+(2x+y)\mathbf{j};
C is the curve \mathbf{r}(t)=t\mathbf{i}+t^{2}\mathbf{j}, 0\leq t\leq 1.
3
\mathbf{F}(x,y)=x^{2}\mathbf{i}+xy\mathbf{j}
C is the curve \mathbf{r}(t)=(\cos t)\mathbf{i}+(\sin t)\mathbf{j}, 0\leq t\leq \pi .
\mathbf{F}(x,y,z)=xy\mathbf{i}+x^{2}z\mathbf{j}+xyz\mathbf{k}
C is the curve \mathbf{r}(t)=e^{t}\mathbf{i}+e^{-t}\mathbf{j}+t^{2} \mathbf{k}, 0\leq t\leq 1.
\displaystyle{3 \over 2}
\mathbf{F}(x,y,z)=y\mathbf{i}+x^{2}y\mathbf{j}+xz\mathbf{k}
C is the curve \mathbf{r}(t)=e^{2t}\mathbf{i}+e^{t}\mathbf{j}+t\mathbf{k}, 0\leq t\leq 1.
In Problems 51–54, for each curve C, find \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} if \mathbf{F}(x,y,z)=xy\mathbf{i}-y \mathbf{j}+z\mathbf{k}.
C is the line segment from (0,0,0) to (1,0,0).
0
C is the line segment from (1,0,0) to (1,2,0).
C is the line segment from (1,2,0) to (1,2,3).
\displaystyle{9 \over 2}
C is the line segment from (0,0,0) to (1,2,3).
In Problems 55–58 find the lateral surface area A of the cylinder that lies above the xy-plane and below the surface z=f(x,y) and is formed by lines parallel to the z-axis and intersecting C.
z=f(x,y)=1-x^{2};\quad C: x=\sin t, y=\cos t, 0\leq t\leq 2\pi
\pi
z=f(x,y)=1-y^{2};\quad C: x=\sin t, y=\cos t, 0\leq t\leq 2\pi
z=f(x,y)=2xy;\quad C: y=\sqrt{1-x^{2}}, 0\leq x\leq 1
1
z=f(x,y)=x+y;\quad C: y=\sqrt{1-x^{2}}, 0\leq x\leq 1
Applications and Extensions
Find \int_{C}\dfrac{\,ds}{x^{2}+y^{2}+z^{2}}, where C is the helix x=a\cos t, y=a\sin t, z=bt, 0\leq t\leq 1.
\displaystyle{{\sqrt {a^2 + b^2} } \over {ab}}\tan ^{ - 1}\left(\displaystyle{b \over a}\right)
Find \int_{C}(y^{n}\,dx+x^{n}\,dy), where C is the ellipse x=a\sin t, y=b\cos t, 0\leq t\leq 2\pi , and n \ge 1 is an integer.
Find \int_{C}y^{2}\,ds, where C is the first arch of the cycloid x=a(t-\sin t), y=a(1-\cos t).
\dfrac{256}{15} a^3
Find \int_{C}\sqrt{x^{2}+y^{2}}\,ds, where C is the curve x=a(\cos t+t\sin t), y=a(\sin t-t\cos t), 0\leq t\leq 2\pi , a > 0.
Find \int_{C}(z\,dx+x\,dy+y\,dz), where C is the circular helix x=a\cos t, y=a\sin t, z=t, 0\leq t\leq 2\pi .
2\pi a + a^2\pi
Find \int_{C}[xz\,dx+(y+z)\,dy+x\,dz], where C is the curve x=e^{t}, y=e^{-t}, z=e^{2t} from t=0 to t=1.
Mass of a Wire In Problems 65 and 66, find the mass M of a thin wire in the shape of the curve C whose variable mass density is \rho .
C: y=x^{2}, 1\leq x\leq 2;\quad \rho =\rho (x,y)=4x
\displaystyle{1 \over 3}(17\sqrt {17} - 5\sqrt 5 )
C: x=3\sin t, y=3\cos t, 0\leq t\leq \dfrac{\pi }{2};\quad \rho =\rho (x,y)=x+y+1
Mass of a Wire Find the mass of a thin wire in the shape of a parabola x=2t^{2}, y=t, -2\leq t\leq 3, if the variable mass density of the wire is \rho (x,y) =3x.
\displaystyle{{387} \over {32}}\sqrt {65} + \displaystyle{3 \over {256}}\ln ( - 8 + \sqrt {65} ) + \displaystyle{{2601} \over {64}}\sqrt {145} - \displaystyle{3 \over {256}}\ln (12 + \sqrt {145} )
Mass of a Wire Find the mass of a thin wire in the shape of a parabola x=t, y=t^{2}-1, 0\leq t\leq 3, if the variable mass density of the wire is \rho (x,y) =x\left( y+1\right) .
Mass of a Wire A spring is made of a thin wire twisted into the shape of a circular helix x=2\cos t, y=2\sin t, z=t. Find the mass of two turns of the spring if the wire has constant mass density \rho.
M = 4\pi \rho \sqrt 5
989
Mass of a Wire A spring is made of a thin wire twisted into the shape of a circular helix x=3\sin t, y=3\cos t, z=t. Find the mass of two turns of the spring if the wire has variable mass density \rho ( x,y,z) =z+2.
Mass of a Wire in Space Write a formula similar to M=\int_{C}\rho (x,y)\, ds for the mass of a thin wire in the shape of a smooth space curve C whose variable mass density is \rho =\rho (x,y,z).
M = \int\limits_C {\rho (x,y,z)\, ds}
In Problems 72–74, use the formula developed in Problem 71 to find the mass of each wire.
Mass of a Wire in Space The thin wire is in the shape of the helix C: x=2\cos t, y=2\sin t, z=5t, 0\leq t\leq 2\pi , whose mass density is \rho (x,y,z)=k, a constant.
Mass of a Wire in Space The thin wire is in the shape of a helix C: x=3\cos t, y=3\sin t, z=4t, 0\leq t\leq 2\pi , whose variable mass density is \rho (x,y,z)=2+z.
M = 20\pi + 40\pi ^2
Mass of a Wire in Space The thin wire is in the shape of a helix C: x=2\cos t, y=2\sin t, z=5t, 0\leq t\leq 2\pi , if the mass density is proportional to the square of the distance from the origin.
Lateral Surface Area Derive the formula A=2\pi Rh for the surface area of a right circular cylinder using the line integral \int_{C}f(x,y)\,ds, where z=f(x,y)=h, h>0, and C is the circle x^{2}+y^{2}=R^{2}.
See Student Solutions Manual.
Let C_{1} be the curve x=\cos \theta , y=\sin \theta , 0\leq \theta \leq 4\pi , and let C_{2} be the curve x=\cos t^{2}, y=\sin t^{2}, 0\leq t\leq 2\sqrt{\pi }. For P(x,y) =x^{3}y and Q(x,y) =y^{2}x, show that \int_{C_{1}}(P\,dx+Q\,dy)=\int_{C_{2}}(P\,dx+Q\,dy). Explain why this is so.
Challenge Problems
Find \int_{C}(x+y)\,ds, where C is the curve x=t, y=\dfrac{3t^{2}}{\sqrt{2}}, 0\leq t\leq 1.
\displaystyle{{19} \over {54}}\sqrt {19} - \displaystyle{1 \over {54}}+\dfrac{37}{96}\sqrt{38}-\dfrac{1}{288}\ln (3\sqrt{2} + \sqrt{19})
Center of Mass Find the center of mass of a homogeneous wire in the shape of the hypocycloid
- (a) x=a\cos ^{3}t,y=a\sin ^{3}t,\ 0\leq t\leq \dfrac{\pi }{2}
- (b) x=a\cos ^{3}t,y=a\sin ^{3}t,\ 0\leq t\leq 2\pi
Suppose the line integral of f(x,y) along the curve C exists.
- (a) Use the Mean Value Theorem to derive the formula \int_{C}f(x,y)\,ds=\int_{a}^{b}f(x(t),y(t))\sqrt{\left( \dfrac{dx}{dt} \right) ^{\!\!2}+\left( \dfrac{dy}{dt}\right) ^{\!\!2}}\,dt
- (b) Apply the formula in (a) to the quantity S(t)=\int_{a}^{t}\sqrt{(x')^2+(y')^2}\,du, where S' (t_{0}) is the length of the portion of the curve traced out as t moves from a to t_{0}.
See Student Solutions Manual.
It follows from Problem 79 that the value of a line integral of a function along a smooth curve, given the hypotheses of the theorem, is independent of the parameterization. Why? In particular, if x and y are differentiable functions of the arc length as one moves along the curve, describe what form the integral \int_{C}f(x,y)\,ds=\int_{a}^{b}f(x(t),y(t)) \sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt}\right) ^{\!\!2}} \,dt
takes when s is used as the parameter.
We have seen two kinds of line integrals: \int_{C}( P\,dx+Q\,dy) and \int_{C}f\,ds. These are closely connected.
- (a) If C is expressed using arc length as the parameter, show that \int_{c}(Pdx + Qdy) can be written in the form \int_{c} fds.
- (b) If the arc length s along C can be expressed as a function of x and y, show that \int_{c}fds can be written in the form \int_{c}(Pdx + Qdy). For example, \int_{C}(x+y^{2})\,ds=\int_{C}\left[\dfrac{x^{2}+xy^{2}}{\sqrt{x^{2}+y^{2}}}\,dx+ \dfrac{xy+y^{3}}{\sqrt{x^{2}+y^{2}}}\,dy\right] where C is the curve x=t, y=t, for 0\leq t\leq 1.
(a and b) See Student Solutions Manual.