15.4 Assess Your UnderstandingPrinted Page 1006
Concepts and Vocabulary
Work is the ____________ transferred to or from an object by a force acting on the object.
Energy
True or False An interpretation of the line integral ∫CF⋅dr is the work done by the force F in moving an object along a piecewise-smooth curve C.
True
True or False The work done by a force F in moving an object from A to B equals the change in the potential energy of the object from A to B.
False
Multiple Choice In a conservative force field F, the work W done by F in moving an object along a closed, piecewise smooth curve C is [(a) a maximum, (b) a minimum, (c) ‖ (d) 0].
(d)
1007
Kinetic energy K is the energy of ____________; potential energy U is the energy of ____________.
motion; position
True or False In a conservative force field \mathbf{F}, the difference of the potential energy U and the kinetic energy K equals 0.
False
Skill Building
In Problems 7–16, find the work done by the force field \mathbf{F} in moving an object along each curve between the indicated points.
\mathbf{F}=y\mathbf{i}+x\mathbf{j} along \mathbf{r}(t)=t \mathbf{i}+t^{2}\mathbf{j} from t=0 to t=1
1
\mathbf{F}=xy\mathbf{i}+y^{2}\mathbf{j} along \mathbf{r} (t)=t\mathbf{i}+t^{2}\mathbf{j} from t=0 to t=1
\mathbf{F}=(x-2y)\mathbf{i}+xy\mathbf{j} along \mathbf{r} (t)=3\cos t\,\mathbf{i}+2\sin t\,\mathbf{j} from t=0 to t=\dfrac{\pi }{2}
3\pi - \displaystyle{1 \over 2}
\mathbf{F}=x\mathbf{i}-y\mathbf{j} along \mathbf{r} (t)=\cos t\,\mathbf{i}+\sin t\,\mathbf{j} from t=0 to t=2\pi
\mathbf{F}=x^{2}y\mathbf{i}+(x^{2}-y^{2})\mathbf{j} along y=2x^{2} from (0,0) to (1,2)
- \displaystyle{{19} \over {15}}
\mathbf{F}=y\sin x\,\mathbf{i}-x\cos y\,\mathbf{j} along y=x from (0,0) to (1,1)
\mathbf{F}=(y-x^{2})\mathbf{i}+x\mathbf{j} along the upper half of the circle x^{2}+y^{2}=1 from (1,0) to (-1,0)
\displaystyle{2 \over 3}
\mathbf{F}=(y-x^{2})\mathbf{i}+x\mathbf{j} along the line segments joining (1,0) to (1,1) to (-1,1) to (-1,0)
\mathbf{F}=y^{3}\mathbf{i}+x^{3}\mathbf{j} along the ellipse \mathbf{r}(t)=a\cos t\,\mathbf{i}+b\sin t\,\mathbf{j} from t=0 to t=2\pi
\displaystyle{3 \over 4} ab\pi (a^2 - b^2)
\mathbf{F}=-y^{2}\mathbf{i}+x^{2}\mathbf{j} along the upper half of the ellipse \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 from (a,0) to (-a,0)
In Problems 17–20, find the work done by each force field \mathbf{F} in moving an object along the curve pictured in each graph.
\mathbf{F}=3x\mathbf{i}+2y\mathbf{j}
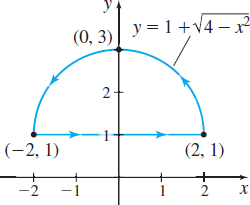
0
\mathbf{F}=2xy\mathbf{i}+xy^{2}\mathbf{j}

\mathbf{F}=e^{x}y\mathbf{i}+e^{x}\mathbf{j}
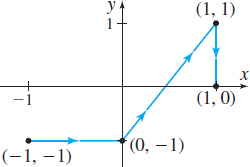
\displaystyle{1 \over e}
\mathbf{F}=e^{x}\mathbf{i}+5y\mathbf{j}
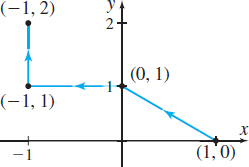
Applications and Extensions
Verify that the force field \mathbf{F}=y\mathbf{i} -x\mathbf{j} is not a conservative vector field. Show that the integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} is dependent on the path of integration by taking two paths in which the starting point is the origin (0,0) and the endpoint is (1,1). For one path, take the line x=y. For the other path, take the x-axis out to the point (1,0) and then the line x=1 up to the point (1,1).
\int\limits_C {{{\bf F}} \cdot d{{\bf r}}} along the first path is 0. \int\limits_C {{{\bf F}} \cdot d{{\bf r}}} along the second path is -1.
Work Find the work done by a variable force \mathbf{F} (x,y) =( x^{2}\mathbf{i}+y\mathbf{j}) to move an object along C traced out by the parametric equations x=t, y=t^{2}, 0\leq t\leq 3.
Work Find the work done by a variable force \mathbf{F} (x,y) =\left( \cos x\mathbf{i}+\sin y\mathbf{j}\right) to move an object along the curve C traced out by the parametric equations x=t, y=\sqrt{t}, 0\leq t\leq \pi.
1 - \cos \sqrt \pi
Work An object moves in a clockwise direction from the origin to the point (2a,0) along the upper half of the circle (x-a)^{2}+y^{2}=a^{2} and is acted upon by a force \mathbf{F} with constant magnitude 3 and with direction \mathbf{i}+\mathbf{j}. Find the work W done by this force.
Work An object moves along the curve \mathbf{r}(t)=64\sqrt{3}t\,\mathbf{i}+(64t-16t^{2})\mathbf{j} from t=0 to t=4 and is acted upon by a force \mathbf{F} whose magnitude is directly proportional to the speed of the object and whose direction is opposite to that of the velocity. Find the work W done by this force.
The work done is -\dfrac{163{,}840}{3}k, where k is a constant of proportionality.
Minimizing Work An object moves from the point (0,0) to the point (1,0) along the curve y=ax(1-x) and is acted upon by a force given by \mathbf{F}(x,y)=(y^{2}+1)\mathbf{i}+(x+y)\mathbf{j}. Find a so that the work W done is a minimum.
Molecular Work The repelling force between a charged particle P at the origin and an oppositely charged particle Q at (x,y) is \mathbf{F}(x,y)=\dfrac{x}{(x^{2}+y^{2})^{3/2}}\mathbf{i}+\dfrac{y}{ (x^{2}+y^{2})^{3/2}}\mathbf{j}
Find the work done by \mathbf{F} as Q moves along the line segment from (1,0) to (-1,2).
1 - \displaystyle{{\sqrt 5 } \over 5}
Work Find the work W done by the force field \mathbf{F} ( x,y,z) =x\mathbf{i}+y\mathbf{j}+\mathbf{k} in moving an object along the helix \mathbf{r}=\mathbf{r}(t) =\sin t\,\mathbf{i}+\cos t\mathbf{j}+t\mathbf{k}, 0\leq t\leq \pi.
Work Find the work W done by the force field \mathbf{F} ( x,y,z) =x^{2}\mathbf{i}+y^{2}\mathbf{j}+z^{2}\mathbf{k} in moving an object along the helix \mathbf{r}=\mathbf{r}(t)=2\cos t\,\mathbf{i}+2\sin t\mathbf{j}+2t\mathbf{k}, 0\leq t\leq \pi.
\displaystyle{8 \over 3}\pi ^3 - \displaystyle{{16} \over 3}
Work Suppose sea level is the xy-plane and the z-axis points upward. Then the gravitational force on an object of mass m near sea level may be taken to be \mathbf{F}=mg\mathbf{k}, where g is the acceleration due to gravity. Show that the work done by gravity on an object moving from (x_{1},y_{1},z_{1}) to (x_{2},y_{2},z_{2}) along any path is W=mg(z_{2}-z_{1}).
Work
- (a) Suppose an object travels through a force field along a path that is always normal to the force. Show that the work done in moving the object from one point to another is 0.
- (b) Why does it follow that the gravitational field of the earth does no work on a satellite in circular orbit?
See Student Solutions Manual.
Work Show that if the work done by a force \mathbf{F}(x,y) in moving an object along any piecewise-smooth, closed curve in an open set S in the plane is 0, then the work done by \mathbf{F} in moving an object from a point A to a point B in S is independent of the piecewise-smooth path chosen.
1008
Challenge Problems
Escape Speed
- (a)
Show that the minimum speed needed to escape from the surface of a planet of mass M in kilograms and radius R in meters is v_{esc}=\sqrt{\dfrac{2GM}{R}}, where G=6.67\times 10^{-11} {\rm N} {\rm m}^{2}/ {\rm kg}^{2}.
This speed is called the escape speed for the planet.
(Hint: Use the relationship between kinetic energy K and the work W done by a force \mathbf{F}.)
- (b) Find the escape speed for Earth (in kilometers per second) using M_{\rm Earth}=5.97\times 10^{24} {\rm kg} and R_{\rm Earth}=6.38\times 10^{6} {\rm m}.
- (c) Find the escape speed for Mars (in kilometers per second) using M_{\rm Mars}=6.42\times 10^{23} {\rm kg} and R_{\rm Mars}=3.40\times 10^{6}{\rm m}.
- (d) Find the escape speed for the Sun (in kilometers per second) using M_{\rm Sun}=1.99\times 10^{30} {\rm kg} and R_{\rm Sun}=6.96\times 10^{8} {\rm m}.
- (a)
- (a) See Student Solutions Manual.
- (b) The escape speed for Earth is 11.2 kilometers per second.
- (c) The escape speed for Mars is 5.0 kilometers per second.
- (d) The escape speed for the sun is 617.6 kilometers per second.
