Differential Equations

16.5 Assess Your Understanding
Printed Page 1093

Skill Building

In Problems 1–12, use power series to solve each differential equation.

$y^{\prime} +3xy=0$

$y(x) = a_0 \sum\limits_{k = 0}^\infty {\left( { - \displaystyle{3 \over 2}} \right)^k} \displaystyle{{x^{2k}} \over {k!}}$

$y^{\prime} -x+3xy=0$

$y^{\prime \prime}+y=0$

$y(x) = a_0 \sum\limits_{k = 0}^\infty {\left( { - 1} \right)^k} \displaystyle{{x^{2k}} \over {(2k)!}} + a_1 \sum\limits_{k = 0}^\infty {\left({ - 1} \right)^k} \displaystyle{{x^{2k + 1}} \over {(2k + 1)!}}$

$y^{\prime \prime} +xy=0$

$y^{\prime \prime} +x^{2}y=0$

$\begin{eqnarray*} y(x) &=& a_0 \left( {1 - \displaystyle{{x^4} \over {3\,{\bf \cdot}\,4}} + \displaystyle{{x^8} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,7\,{\bf \cdot}\,8}} - \displaystyle{{x^{12}} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,7\,{\bf \cdot}\,8\,{\bf \cdot}\,11\,{\bf \cdot}\,12}} + \displaystyle{{x^{16}} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,7\,{\bf \cdot}\,8\,{\bf \cdot}\,11\,{\bf \cdot}\,12\,{\bf \cdot}\,15\,{\bf \cdot}\,16}} - \cdots } \right)\\ &&+ a_1 \left( {x - \displaystyle{{x^5} \over {4\,{\bf \cdot}\,5}} + \displaystyle{{x^9} \over {4\,{\bf \cdot}\,5\,{\bf \cdot}\,8\,{\bf \cdot}\,9}} - \displaystyle{{x^{13}} \over {4\,{\bf \cdot}\,5\,{\bf \cdot}\,8\,{\bf \cdot}\,9\,{\bf \cdot}\,12\,{\bf \cdot}\,13}} + \displaystyle{{x^{17}} \over {4\,{\bf \cdot}\,5\,{\bf \cdot}\,8\,{\bf \cdot}\,9\,{\bf \cdot}\,12\,{\bf \cdot}\,13\,{\bf \cdot}\,16\,{\bf \cdot}\,17}} - \cdots } \right) \end{eqnarray*}$

$y^{\prime \prime} -2xy=0$

$y^{\prime \prime} +x^{2}y^{\prime} +xy=0$

$\begin{eqnarray*} y(x) &=& a_0 \left( {1 - \displaystyle{{1\,{\bf \cdot}\,x^3} \over {2\,{\bf \cdot}\,3}} + \displaystyle{{1\,{\bf \cdot}\,4\,{\bf \cdot}\,x^6} \over {2\,{\bf \cdot}\,3\,{\bf \cdot}\,5\,{\bf \cdot}\,6}} - \displaystyle{{1\,{\bf \cdot}\,4\,{\bf \cdot}\,7\,{\bf \cdot}\,x^9} \over {2\,{\bf \cdot}\,3\,{\bf \cdot}\,5\,{\bf \cdot}\,6\,{\bf \cdot}\,8\,{\bf \cdot}\,9}} + \displaystyle{{1\,{\bf \cdot}\,4\,{\bf \cdot}\,7\,{\bf \cdot}\,10\,{\bf \cdot}\,x^{12}} \over {2\,{\bf \cdot}\,3\,{\bf \cdot}\,5\,{\bf \cdot}\,6\,{\bf \cdot}\,8\,{\bf \cdot}\,9\,{\bf \cdot}\,11\,{\bf \cdot}\,12}} - \cdots } \right)\\ &&+ a_1 \left( {x - \displaystyle{{2\,{\bf \cdot}\,x^4} \over {3\,{\bf \cdot}\,4}} + \displaystyle{{2\,{\bf \cdot}\,5\,{\bf \cdot}\,x^7} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,6\,{\bf \cdot}\,7}} - \displaystyle{{2\,{\bf \cdot}\,5\,{\bf \cdot}\,8\,{\bf \cdot}\,x^{10}} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,6\,{\bf \cdot}\,7\,{\bf \cdot}\,9\,{\bf \cdot}\,10}} + \displaystyle{{2\,{\bf \cdot}\,5\,{\bf \cdot}\,8\,{\bf \cdot}\,11\,{\bf \cdot}\,x^{13}} \over {3\,{\bf \cdot}\,4\,{\bf \cdot}\,6\,{\bf \cdot}\,7\,{\bf \cdot}\,9\,{\bf \cdot}\,10\,{\bf \cdot}\,12\,{\bf \cdot}\,13}} - \cdots } \right) \end{eqnarray*}$

$y^{\prime \prime} +3xy^{\prime} +3y=0$

$y^{\prime \prime \prime} +y=0$

$\begin{eqnarray*} y(x) &=& a_0 \left( {1 - \displaystyle{{x^3} \over {3!}} + \displaystyle{{x^6} \over {6!}} - \displaystyle{{x^9} \over {9!}} + \displaystyle{{x^{12}} \over {12!}} - \cdots } \right) + a_1 \left( {x - \displaystyle{{x^4} \over {4!}} + \displaystyle{{x^7} \over {7!}} - \displaystyle{{x^{10}} \over {10!}} + \displaystyle{{x^{13}} \over {13!}} - \cdots } \right)\\ &&+ a_2 \left( {x^2 - \displaystyle{{2\,{\bf \cdot}\,x^5} \over {5!}} + \displaystyle{{2\,{\bf \cdot}\,x^8} \over {8!}} - \displaystyle{{2\,{\bf \cdot}\,x^{11}} \over {11!}} + \displaystyle{{2\,{\bf \cdot}\,x^{14}} \over {14!}} - \cdots } \right) \end{eqnarray*}$

$y^{\prime \prime \prime} -xy=0$

$(1+x^{2})y^{\prime \prime} -4xy^{\prime} +6y=0$

$y(x) = a_0 \left( {1 - 3x^2} \right) + a_1 \left( {x - \dfrac{1}{3}x^3} \right)$

$(x^{2}+2)y^{\prime \prime} -3xy^{\prime} +4y=0$

In Problems 13–22:

(a) Use a Maclaurin series to find the solution of each differential equation using the given initial conditions.
(b) Use the first five nonzero terms of the series to approximate values of $y$ for $0\leq x\leq 1.$ Use Table 1 as a guide.

$y^{\prime \prime} +xy^{\prime} +y=0; \quad y(0)=1, \quad y^{\prime}(0)=0$

$y(x) = 1 - \displaystyle{1 \over {2!}}x^2 + \displaystyle{3 \over {4!}}x^4 - \displaystyle{{15} \over {6!}}x^6 + \displaystyle{{105} \over {8!}}x^8 - \cdots$
(b)

$x$ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

$y(x)$ 1.0000 0.9950 0.9802 0.9560 0.9231 0.8825 0.8353 0.7827 0.7262 0.6671 0.6068

$y^{\prime \prime} -2xy^{\prime} +y=0; \qquad y(0)=2, \quad y^{\prime} (0)=1$

$y^{\prime \prime} -(\sin x)y=0; \qquad y(0)=0, \quad y^{\prime} (0)=1$

$y(x) = x + \displaystyle{2 \over {4!}}x^4 - \displaystyle{4 \over {6!}}x^6 + \displaystyle{{10} \over {7!}}x^7 + \displaystyle{6 \over {8!}}x^8 + \cdots$
(b)

$x$ 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

$y(x)$ 0 0.100008 0.2001 0.3007 0.4021 0.5051 0.6106 0.7195 0.8331 0.9527 1.0799

$y^{\prime \prime} +(\cos x)y=0; \qquad y(0)=0, \quad y^{\prime} ( 0) =1$

$y^{\prime \prime} +y^{\prime} +e^{x}y=0; \qquad y( 0) =2, \quad y^{\prime} ( 0) =1$

$y(x) = 2 + x - \displaystyle{3 \over {2!}}x^2 - \displaystyle{1 \over {4!}}x^4 + \displaystyle{5 \over {5!}}x^5 + \cdots$
(b)

$x$ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

$y(x)$ 2.0000 2.0850 2.1399 2.1648 2.1594 2.1237 2.0578 1.9620 1.8366 1.6823 1.5000

1094

$y^{\prime \prime} +(3+x)y=0; \qquad y(0)=1, \quad y^{\prime} (0)=0$

$y^{\prime \prime} +x^{2}y=0; \qquad y(0)=0, \quad y^{\prime} (0)=2$

$y(x) = 2x - \displaystyle{{12} \over {5!}}x^5 + \displaystyle{{504} \over {9!}}x^9 - \displaystyle{{55,440} \over {13!}}x^{13} + \displaystyle{{11,642,400} \over {17!}}x^{17} - \cdots$
(b)

$x$ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

$y(x)$ 0.0000 0.2000 0.4000 0.5998 0.7990 0.9969 1.1922 1.3832 1.5674 1.7415 1.9014

$y^{\prime \prime} -3x^{2}y^{\prime} +2xy=0; \qquad y(0)=1, \quad y^{\prime }(0)=1$ ,

$y^{(4)}-\ln (1+x)y=0; \qquad y(0)=1$ , $y^{\prime} (0)=1, \quad y^{\prime \prime} (0)=0, \quad y^{\prime \prime \prime} (0)=0$

$y(x) = 1 + x + \displaystyle{1 \over {5!}}x^5 + \displaystyle{1 \over {6!}}x^6 - \displaystyle{1 \over {7!}}x^7 + \cdots$
(b)

$x$ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

$y(x)$ 1.0000 1.1000 1.2000 1.3000 1.4001 1.5003 1.6007 1.7015 1.8031 1.9056 2.0095

$y^{\prime \prime \prime} +4y^{\prime \prime} +2y^{\prime} -x^{3}y=0; \qquad y(0)=1, \quad y^{\prime} (0)=1, \quad y^{\prime \prime} ( 0) =0$

Applications and Extensions

Exact and Series Solutions
1. Use the first six terms of a Maclaurin series to approximate the solution of the differential equation $y^{\prime \prime} +4y^{\prime} +4y=0$ with the initial conditions $y( 0) =1$ and $y^{\prime} ( 0) =2$ .
2. (b) Solve the differential equation from (a) using a CAS.
3. Graph both the series solution from (a) and the exact solution from (b) on the interval $[-1,2]$ .
4. (d) Comment on the graphs.
5. (e) Repeat (a) using the first eight terms of a Maclaurin series.
6. (f) Add the solution from (e) to the graph in (c). What is happening?

(a) $y(x) \approx 1 + 2x - 6x^2 + \displaystyle{{20} \over 3}x^3 - \displaystyle{{14} \over 3}x^4 + \displaystyle{{12} \over 5}x^5$

(b) $y(x) = \mbox{e}^{ - 2x}(1 + 4x)$

(d) See Student Solutions Manual.

(e) $y(x) \approx 1 + 2x - 6x^2 + \displaystyle{{20} \over 3}x^3 - \displaystyle{{14} \over 3}x^4 + \displaystyle{{12} \over 5}x^5 - \displaystyle{{44} \over {45}}x^6 + \displaystyle{{104} \over {315}}x^7$

(c and f) The graphs are shown. See Student Solutions Manual for explanation.

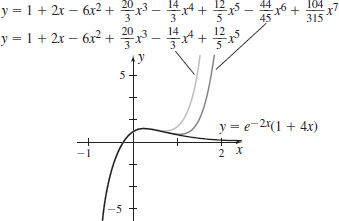
Exact and Series Solutions
1. Use the first six nonzero terms of a Maclaurin series to approximate the solution of the differential equation $y^{\prime} =xy (1-y^{2})$ with the initial condition $y( 0) =2$ .
2. (b) Solve the differential equation from (a) using a CAS.
3. Graph the exact solution from (b) and the series solutions using two, four, and six nonzero terms on the interval $[-2,2]$ .

Challenge Problems

Age of the Earth's Crust. Uranium has a half-life of $4.5\times 10^{9}$ years. The decomposition sequence is very complicated, producing a very large number of intermediate radioactive products, but the final product is an isotope of lead with an atomic weight of 206, called uranium lead.
1. (a)
  Assuming that the change from uranium to lead is direct, show that $u=u_{0}e^{-kt}$ , $\ l=u_{0}(1-e^{-kt})$ , where $u$ and $l$ denote the number of uranium and uranium lead atoms, respectively, present at time $t$ . That is, assume $\dfrac{du}{dt} = -ku$ , where $k > 0$ is a constant, and $l = u_0 - u$ .
  
  We can measure the ratio $r=\dfrac{l}{u}$ in a rock, and if it is assumed that all the uranium lead came from decomposition of the uranium originally present in the rock, we can obtain a lower bound for the age of Earth's crust. Currently, $r \approx 0.054$ .
2. Show that this lower bound is given by $\begin{equation*} t=\frac{1}{k}\ln (1+r)=\frac{1}{k}\left( r-\frac{r^{2}}{2}+\frac{r^{3}}{3} -\cdots \right) > \frac{r}{k} \end{equation*}$
3. (c) What is this lower bound?

(a) See Student Solutions Manual.
(b) See Student Solutions Manual.
The lower bound is $3.506 \times 10^{8}$ years.

$x$	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$y(x)$	1.0000	0.9950	0.9802	0.9560	0.9231	0.8825	0.8353	0.7827	0.7262	0.6671	0.6068

$x$	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$y(x)$	0	0.100008	0.2001	0.3007	0.4021	0.5051	0.6106	0.7195	0.8331	0.9527	1.0799

$x$	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$y(x)$	2.0000	2.0850	2.1399	2.1648	2.1594	2.1237	2.0578	1.9620	1.8366	1.6823	1.5000

$x$	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$y(x)$	0.0000	0.2000	0.4000	0.5998	0.7990	0.9969	1.1922	1.3832	1.5674	1.7415	1.9014

$x$	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$y(x)$	1.0000	1.1000	1.2000	1.3000	1.4001	1.5003	1.6007	1.7015	1.8031	1.9056	2.0095

16.5 Assess Your UnderstandingPrinted Page 1093

16.5 Assess Your Understanding
Printed Page 1093